2021-2022学年人教版数学八年级下册19.2.3 一次函数与方程、不等式 课件(共22张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册19.2.3 一次函数与方程、不等式 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 893.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 11:21:10 | ||
图片预览






文档简介
(共22张PPT)
19.2.3 一次函数与方程、不等式
(1)一次函数与一元一次方程
(2)一次函数图象应用——不同出发地行程问题
人教版数学八级下册
一次函数与一元一次方程
一次函数与一元一次方程
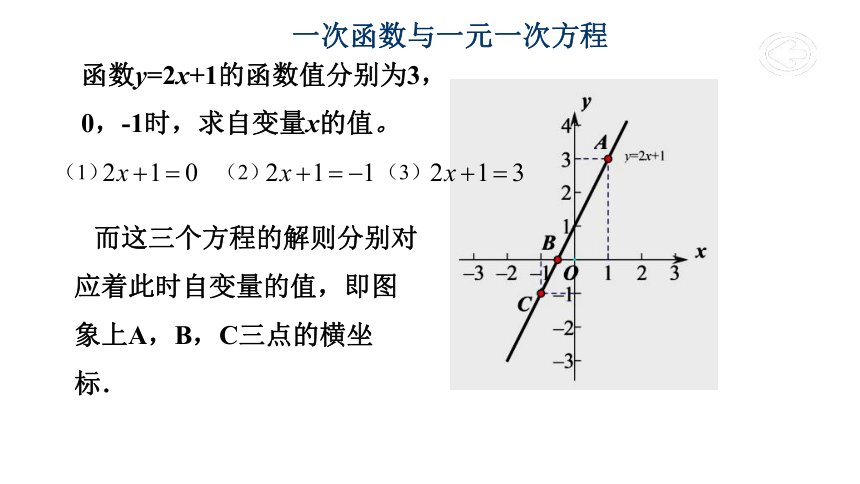
而这三个方程的解则分别对应着此时自变量的值,即图象上A,B,C三点的横坐标.
函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值。
(1) (2) (3)
分
析
从函数的角度看,解这三个方程
方程2x+1=3的解是: ;
即当 时,函数y=2x+1的值为3,也就是 ;
方程2x+1=-1的解是: ;
即当 时,函数y=2x+1的值为-1,也就是 .
方程2x+1=0的解是: ;
即当 时,函数y=2x+1的值为0,也就是 ;
x=1
x=-1
x=1
y=3
x=
y=0
x=-1
y=-1
x=
方程
函数
发
现
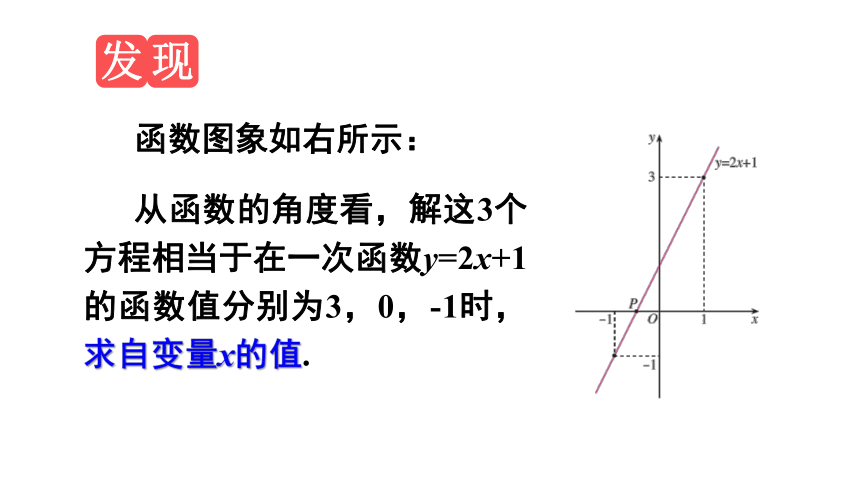
从函数的角度看,解这3个方程相当于在一次函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值.
函数图象如右所示:
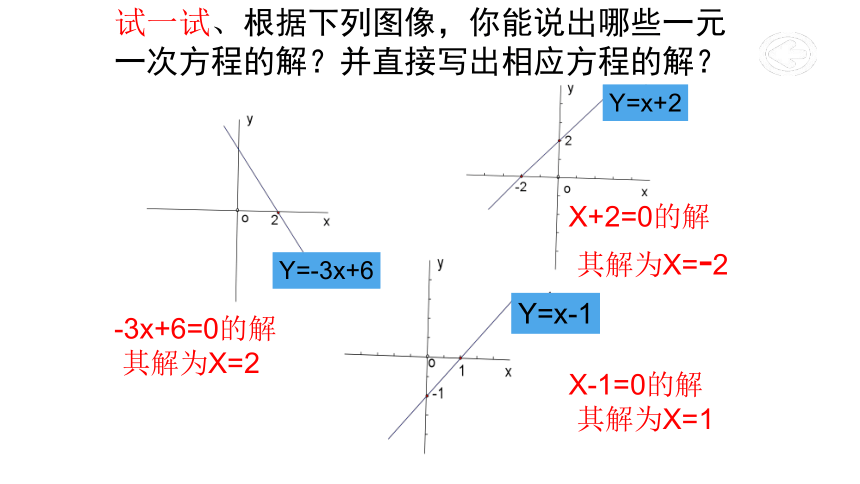
试一试、根据下列图像,你能说出哪些一元一次方程的解?并直接写出相应方程的解?
X+2=0的解
其解为X=-2
-3x+6=0的解
其解为X=2
X-1=0的解
其解为X=1
Y=x+2
Y=-3x+6
Y=x-1
一元一次方程都可以转化为_________ 的形式.
kx+b=0
0
自变量x
求直线y=kx+b与 的交点的 坐标.
x轴
横
当一次函数y=kx+b的值为 时,求相应的_______
的值.
求方程kx+b=0的解
规律总结
应用新知
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米,再过几秒它的速度为17米/秒?
解法1:设再过x秒物体的速度为17米/秒.
列出方程 2x+5=17
解得x=6.
应用新知
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米,再过几秒它的速度为17米/秒?
解法2:将解法1中的方程化为2x-12=0,
画出函数y=2x-12的图象,
找到图象与x轴的交点(6,0),
得x=6.
例.利用函数图象解出x:
5x 1= 2x+5
解:
由 5x 1=2x+5,
得 3x 6=0 .
x
y
6
O
y=3x 6
2
由图看出直线y = 3x 6与x轴的交点为(2,0),得x=2.
一次函数与一元一次方程
作出函数y = 3x 6的图像
一次函数与一元一次方程:
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时
函数y= ax+b的值
为0.
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b
与 x 轴交点的横
坐标.
从“形”的角度看
一次函数图象应用
——不同出发地行程问题
导入初读函数图像再读函数图像
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,相向而行.快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
知识讲解
难点突破
细读函数图像 解决实际问题
1.快、慢两车行驶的速度各是多少?
建立函数模型 解决实际问题
2.D的实际含义是什么?出发多少小时快、慢两车距各自出发地的路程相等
解∵ B(4,360)C(7,0)
设BC解析式为y=kx+b,
解得:k=﹣120
∴ BC解析式为:y=﹣120x+840(4≤x≤7)
设OE解析式为:y=ax∴360=6a,解得:a=60
∴ OE解析式为:y=60x(0≤x≤6)
即 60x=﹣120x+840,x=14/3
当出发14/3小时快慢两车距各自出发地的路程相等。
即为D的实际含义。
慢车到达甲地前,快慢两车相距为150千米的图象。
将慢车y值改成离甲地的距离,快慢两车y值含义相同,函数值相减即可。
理解运动状态 难点解决
3.慢车到达甲地前,何时快慢两车相距为150千米?
慢车到达甲地前,何时快慢两车相距为150千米?
两车相遇前可以相距150km
﹣60x+360﹣120x=150
相遇后两车再次相距150km
120x-(-60x+360)=150
当快车到达乙地后返回时两车可以相距150km
﹣120x+840-(-60x+360)=150
课堂练习难点巩固快慢两车从相距360千米路程的甲乙两地同时出发,匀速行驶,相向而行.快车到达乙地后,立即按原路返回,快车比慢车早0.6小时到达甲地,快慢两车距甲的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.请结合图象信息解答下列问题:(1)快车往返的速度各是多少?慢车的速度是多少?(2)出发多少小时,快慢两车相遇?(3)请直接说出快车到达甲地前,快慢两车相距为150千米的次数.【课堂小结】
小结
老师赠言
时间是一个常量,但对勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业。
你的收获与平时的付出是成正比的,一份耕耘,一份收获。相信自己,只要付出,你一定会有收获!
感 谢 聆 听
19.2.3 一次函数与方程、不等式
(1)一次函数与一元一次方程
(2)一次函数图象应用——不同出发地行程问题
人教版数学八级下册
一次函数与一元一次方程
一次函数与一元一次方程
而这三个方程的解则分别对应着此时自变量的值,即图象上A,B,C三点的横坐标.
函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值。
(1) (2) (3)
分
析
从函数的角度看,解这三个方程
方程2x+1=3的解是: ;
即当 时,函数y=2x+1的值为3,也就是 ;
方程2x+1=-1的解是: ;
即当 时,函数y=2x+1的值为-1,也就是 .
方程2x+1=0的解是: ;
即当 时,函数y=2x+1的值为0,也就是 ;
x=1
x=-1
x=1
y=3
x=
y=0
x=-1
y=-1
x=
方程
函数
发
现
从函数的角度看,解这3个方程相当于在一次函数y=2x+1的函数值分别为3,0,-1时,求自变量x的值.
函数图象如右所示:
试一试、根据下列图像,你能说出哪些一元一次方程的解?并直接写出相应方程的解?
X+2=0的解
其解为X=-2
-3x+6=0的解
其解为X=2
X-1=0的解
其解为X=1
Y=x+2
Y=-3x+6
Y=x-1
一元一次方程都可以转化为_________ 的形式.
kx+b=0
0
自变量x
求直线y=kx+b与 的交点的 坐标.
x轴
横
当一次函数y=kx+b的值为 时,求相应的_______
的值.
求方程kx+b=0的解
规律总结
应用新知
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米,再过几秒它的速度为17米/秒?
解法1:设再过x秒物体的速度为17米/秒.
列出方程 2x+5=17
解得x=6.
应用新知
例1 一个物体现在的速度是5米/秒,其速度每秒增加2米,再过几秒它的速度为17米/秒?
解法2:将解法1中的方程化为2x-12=0,
画出函数y=2x-12的图象,
找到图象与x轴的交点(6,0),
得x=6.
例.利用函数图象解出x:
5x 1= 2x+5
解:
由 5x 1=2x+5,
得 3x 6=0 .
x
y
6
O
y=3x 6
2
由图看出直线y = 3x 6与x轴的交点为(2,0),得x=2.
一次函数与一元一次方程
作出函数y = 3x 6的图像
一次函数与一元一次方程:
求ax+b=0(a,b是
常数,a≠0)的解.
x为何值时
函数y= ax+b的值
为0.
从“数”的角度看
求ax+b=0(a, b是
常数,a≠0)的解.
求直线y= ax+b
与 x 轴交点的横
坐标.
从“形”的角度看
一次函数图象应用
——不同出发地行程问题
导入初读函数图像再读函数图像
快、慢两车分别从相距360千米路程的甲、乙两地同时出发,匀速行驶,相向而行.快车到达乙地后,停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.
知识讲解
难点突破
细读函数图像 解决实际问题
1.快、慢两车行驶的速度各是多少?
建立函数模型 解决实际问题
2.D的实际含义是什么?出发多少小时快、慢两车距各自出发地的路程相等
解∵ B(4,360)C(7,0)
设BC解析式为y=kx+b,
解得:k=﹣120
∴ BC解析式为:y=﹣120x+840(4≤x≤7)
设OE解析式为:y=ax∴360=6a,解得:a=60
∴ OE解析式为:y=60x(0≤x≤6)
即 60x=﹣120x+840,x=14/3
当出发14/3小时快慢两车距各自出发地的路程相等。
即为D的实际含义。
慢车到达甲地前,快慢两车相距为150千米的图象。
将慢车y值改成离甲地的距离,快慢两车y值含义相同,函数值相减即可。
理解运动状态 难点解决
3.慢车到达甲地前,何时快慢两车相距为150千米?
慢车到达甲地前,何时快慢两车相距为150千米?
两车相遇前可以相距150km
﹣60x+360﹣120x=150
相遇后两车再次相距150km
120x-(-60x+360)=150
当快车到达乙地后返回时两车可以相距150km
﹣120x+840-(-60x+360)=150
课堂练习难点巩固快慢两车从相距360千米路程的甲乙两地同时出发,匀速行驶,相向而行.快车到达乙地后,立即按原路返回,快车比慢车早0.6小时到达甲地,快慢两车距甲的路程y(千米)与出发后所用的时间x(小时)的关系如图所示.请结合图象信息解答下列问题:(1)快车往返的速度各是多少?慢车的速度是多少?(2)出发多少小时,快慢两车相遇?(3)请直接说出快车到达甲地前,快慢两车相距为150千米的次数.【课堂小结】
小结
老师赠言
时间是一个常量,但对勤奋者来说,却是一个“变量”,我们应当在有限的时间内做出伟大的事业。
你的收获与平时的付出是成正比的,一份耕耘,一份收获。相信自己,只要付出,你一定会有收获!
感 谢 聆 听
