2021-2022学年湘教版八年级数学下册2.5矩形知识点分类训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学下册2.5矩形知识点分类训练(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 388.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览

文档简介
2021-2022学年湘教版八年级数学下册《2-5矩形》知识点分类训练(附答案)
一.矩形的性质
1.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的长方形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其它两个顶点在长方形的边上,则剪下的等腰三角形的面积为( )平方厘米.
A.50或60 B.40或50或80 C.30或40或50 D.30或50或80
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
3.如图,在矩形ABCD中,点F为边AD上一点,过F作EF∥AB交边BC于点E,P为边AB上一点,PH⊥DE交线段DE于H,交线段EF于Q,连接DQ.当AF=AB时,要求阴影部分的面积,只需知道下列某条线段的长,该线段是( )
A.EF B.DE C.PH D.PE
4.如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是( )
A.α=β B.α=γ C.α+β+2γ=90° D.2α+γ=90°
5.在矩形ABCD中,点A关于∠B的角平分线的对称点为E,点E关于∠C的角平分线的对称点为F.若AD=,AB=1,则AF2=( )
A.8﹣4 B.10﹣4 C.8+4 D.10+4
6.如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连接DF,M为DF的中点,连接MA,ME.若AM⊥ME,则AE的长为( )
A.5 B. C. D.
7.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45° B.60° C.75° D.30°
8.已知点P是矩形ABCD内一点,连接AP、BP、CP、DP,若S△ABP+S△CDP=S△ADP+S△BCP,则关于点P的位置,正确的说法是( )
A.一定是对角线交点 B.一定在对角线上
C.一定在对边中点的连线上 D.可以是任意位置
9.如图是一块矩形ABCD的场地,长AB=102,宽AD=51,从A、B两处入口的中路宽都为1,两小路汇合处路宽为2,其余部分种植草坪,则草坪面积为( )
A.5050 B.4900 C.5000 D.4998
10.如图,矩形ABCD中,对角线AC,BD交于点O,点E是边AB上一点,且OE⊥AC.设∠AOD=α,∠AEO=β,则α与β间的关系正确的是( )
A.α=β B.α+β=180° C.2α+β=180° D.α+2β=180°
11.如图,矩形ABCD中,E,F是CD上的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=( )
A.+1 B. C.3 D.
12.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于点E,DF平分∠ADC,交EB的延长线于点F,BC=6,CD=3,则为( )
A. B. C. D.
13.如图所示,P是矩形ABCD内的任意一点,连接PA,PB,PC,PD,得到△PAB,△PBC,△PCD,△PDA,设它们的面积分别是S1,S2,S3,S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
15.矩形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积为 .
16.如图,矩形ABCD中,,连结对角线AC,E为AC的中点,F为边AB上的动点,连结EF,作点C关于直线EF的对称点C′,连结C′E,C′F,CF,若△EFC′与△ACF重叠部分面积等于△ACF面积的,则AG EG(填“>”、“=”或“<”),BF= .
17.如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为 .
18.如图,在矩形ABCD中对角线AC,BD交于点O,DE平分∠ADC交AB于点E,连接OE,若AD=6,AB=8,则OE= .
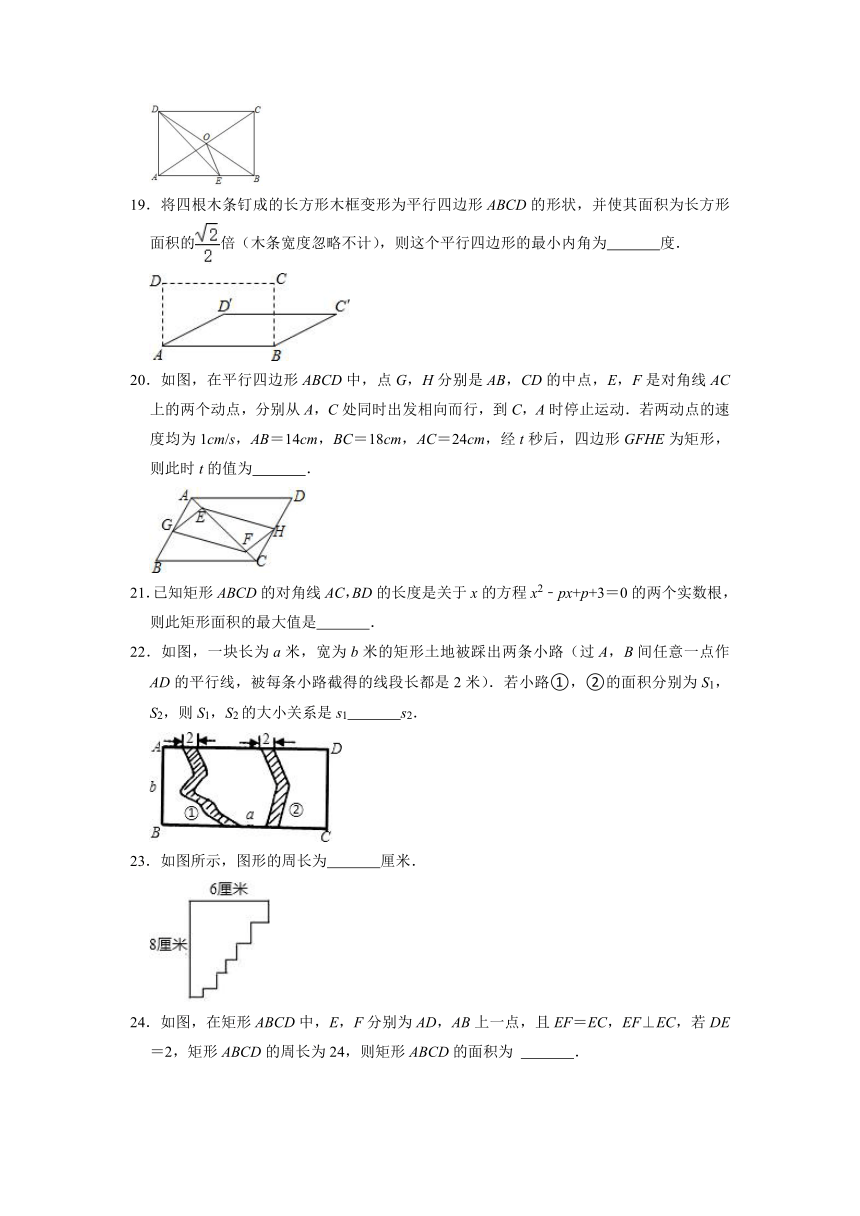
19.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的倍(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,E,F是对角线AC上的两个动点,分别从A,C处同时出发相向而行,到C,A时停止运动.若两动点的速度均为1cm/s,AB=14cm,BC=18cm,AC=24cm,经t秒后,四边形GFHE为矩形,则此时t的值为 .
21.已知矩形ABCD的对角线AC,BD的长度是关于x的方程x2﹣px+p+3=0的两个实数根,则此矩形面积的最大值是 .
22.如图,一块长为a米,宽为b米的矩形土地被踩出两条小路(过A,B间任意一点作AD的平行线,被每条小路截得的线段长都是2米).若小路①,②的面积分别为S1,S2,则S1,S2的大小关系是s1 s2.
23.如图所示,图形的周长为 厘米.
24.如图,在矩形ABCD中,E,F分别为AD,AB上一点,且EF=EC,EF⊥EC,若DE=2,矩形ABCD的周长为24,则矩形ABCD的面积为 .
25.如图,长方形ABCD中,AB=4,AD=3,长方形内有一个点P,连接AP,BP,CP,已知∠APB=90°,CP=CB,延长CP交AD于点E,则AE= .
26.如图,矩形ABCD的面积为16cm2,它的两条对角线交于点O1,以AB、AO1为邻边作 ABC1O1,设 ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作 ABC2O2,…,依此类推,则 ABC6O6的面积为 cm2.
27.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,求矩形ABCD长与宽的比值.
28.如图,在矩形ABCD中,E是BC上一点,DF⊥AE于点F,设=λ(λ>0).若λ=1,求证:CE=FE;
29.如图,将一长方形纸片ABCD沿着EF折叠,已知AF∥BE,DF∥CE,CE交AF于点G,过点G作GH∥EF,交线段BE于点H.
(1)判断∠CGH与∠DFE是否相等,并说明理由;
(2)①判断GH是否平分∠AGE,并说明理由;
②若∠DFA=52°,求∠HGE的度数.
30.如图,在 ABCD中,点E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.
二.矩形的判定
31.已知Rt△ABC,∠ABC=90°,小明按如下步骤作图,①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;②连接DA,DC,则四边形ABCD为 .
32.如图,将 ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:四边形ABEC是平行四边形;
(2)若∠AFC=2∠ADC,求证:四边形ABEC是矩形.
33.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
34.已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
35.如图,在△ABC中,D是BC边上的中点,过A点作AF∥BC,且AF=BD,连接CF交AD于点E.
(1)求证:AE=ED;
(2)若AB=AC,试判断四边形AFBD形状,并说明理由.
36.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
37.已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
三.矩形的判定与性质
38.如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上的动点(不与B,C重合)过点D作DE⊥AB于点E,作DF⊥AC于点F,则EF的最小值是( )
A.3 B. C.5 D.
39.如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
40.如图,已知 ABCD,延长AB到E,使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=6,CD=3,求AC的长.
41.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
42.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
43.如图,在平行四边形ABCD中,点M,N是AD边上的点,BM,CN交于点O,AN=DM,BM=CN.
(1)求证:平行四边形ABCD是矩形.
(2)若∠BOC=90°,MN=1,AM MD=12,求矩形ABCD的面积.
44.如图,平行四边形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F,且AE=DF.
(1)求证:四边形ABCD是矩形.
(2)若∠BAE:∠EAD=2:3,求∠EAO的度数.
参考答案
一.矩形的性质
1.解:分三种情况讨论:
①如图1所示:
BE=BF=10,
等腰三角形的面积=10×10÷2=50(cm2);
②如图2所示:
BE=16﹣10=6(cm),
BF==8(cm),
等腰三角形的面积=10×8÷2=40(cm2);
③如图3所示:
DE=18﹣10=8(cm),
DF==6(cm),
等腰三角形的面积=10×6÷2=30(cm2).
故选:C.
2.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC=30°,∠EDA=60°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DAC=30°,
∴DC=AC=4,
∴EC=DC=2,
故选:B.
3.解:过点P作PM⊥EF于点M,如图:
∵四边形ABCD为矩形,
∴AB∥DC,AD∥BC,∠C=90°,
∵EF∥AB,
∴EF∥DC,
∴∠EDC=∠DEF,
∵PH⊥DE,PM⊥EF,
∴∠PMQ=∠EHQ=90°,
又∵∠PQM=∠EQH,
∴∠QPM=∠DEF=∠EDC,
在△PMQ和△DCE中,
,
∴△PMQ≌△DCE(ASA),
∴PQ=DE,
∴阴影部分的面积=S△PDE﹣S△QED=×DE×PH﹣DE×QH=DE2,
∴故选:B.
4.解:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵∠ADE=α,∠EDF=β,∠FDC=γ,
∴α+β+γ=90°,
∵∠AED+α=90°,∠AED=α+β,
∴2α+β=90°,
∴α+β+γ=2α+β,
∴α=γ,
故选:B.
5.解:∵四边形ABCD是矩形,
∴AB=CD=1,BC=AD=,
∵点A关于∠B的角平分线的对称点为E,点E关于∠C的角平分线的对称点为F,
∴AB=BE=1,CE=CF=﹣1,
∴DF=CD﹣CF=2﹣,
∴AF2=AD2+DF2=3+7﹣4=10﹣4,
故选:B.
6.解:∵四边形ABCD是矩形,
∴∠DAF=90°,
∵EF⊥DE,
∴∠DEF=90°,
∵FM=DM,
∴AM=EM=DF=×=,
∵AM⊥ME,
∴∠AME=90°,
∴AE===2,
故选:B.
7.解:∵四边形ABCD是矩形,
∴AO=BO,∠BAD=∠ABE=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
又∵∠CAE=15°,
∴∠BAO=45°+15°=60°,
∴△ABO是等边三角形,
∴AB=BO,
又∵∠BAE=45°=∠AEB,
∴AB=EB,
∴BO=BE,
∴∠BOE==75°,
∴∠COE=180°﹣∠AOB﹣∠BOE=180°﹣60°﹣75°=45°,
故选:A.
8.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
作PE⊥AD于E,延长EP交BC于F,如图所示:
则PF⊥BC,EF=AB,
∵△ADP的面积+△BCP的面积=AD PE+BC PF=BC(PE+PF)=BC EF=BC AB,
∴△ADP的面积+△BCP的面积=矩形ABCD的面积,
同理:△ABP的面积+△CDP的面积=矩形ABCD的面积,
∴△ADP的面积+△BCP的面积=△ABP的面积+△CDP的面积;
故选:D.
9.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:102﹣2=100,宽为51﹣1=50.所以草坪的面积应该是长×宽=100×50=5000.
故选:C.
10.解:∵四边形ABCD是矩形,
∴OA=OD,
∴∠OAD=∠ODA,
∵∠AOD=α,
∴∠OAD=(180°﹣α),
∵OE⊥AC,
∴∠AOE=90°,
∵∠AEO=β,∠DAE=90°,
∴∠OAD=∠AEO,
∴(180°﹣α)=β,
∴α+2β=180°.故选:D.
11.解:过点E作EM⊥AB于M,延长EG交AB于Q,则△EQM是直角三角形.
∵EG⊥AC,FH⊥AC,
∴∠CHF=∠AGQ=90°,
∵矩形ABCD中,CD∥AB,
∴∠FCH=∠QAG,
在△FCH和△QAG中,
,
∴△FCH≌△QAG(ASA),
∴AQ=CF=2,FH=QG,
∵∠D=∠DAM=∠AME=90°,
∴四边形ADEM是矩形,
∴AM=DE=1,EM=AD=2,
∴MQ=2﹣1=1,
∴Rt△EMQ中,EQ===,
即EG+QG=EG+FH=.故选:B.
12.证明:∵四边形ABCD为矩形,
∴AC=BD,∠ADC=90°,OA=OD,
∴∠COD=2∠ADO,
又∵BE⊥AC,
∴∠EOB+∠EBO=90°,
∵∠EBO=∠BDF+∠F,
∴2∠ADO+∠BDF+∠F=90°,
又∵DF平分∠ADC,
∴∠ADO+∠BDF=∠ADC=45°,
∴2∠ADO+∠BDF+∠F=45°+∠ADO+∠F=90°,
∴∠ADO+∠F=45°,
又∵∠BDF+∠ADO=45°,
∴∠BDF=∠F,
∴BF=BD,
∴AC=BF,
∵BC=6,CD=3,
∴AD=6,
∴BF=AC==3,
∵S△ABC=AC BE=AB BC,
∴BE=,
∴==,
故选:C.
13.解:如图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3=矩形ABCD面积;
同理可得出S2+S4=矩形ABCD面积;
∴②S2+S4=S1+S3正确;
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4.
但P是矩形ABCD内的任意一点,所以该等式不一定成立.
故①不一定正确;
③若S3=2S1,只能得出△APB与△PDC高度之比,S4不一定等于2S2;
故此选项错误;
∵S2+S4=S1+S3;若S1=S2,则S3=S4,
∴④正确.故选:B.
14.解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=AB,
∵AD=AB,
∴AE=AD,
在△ABE和△AHD中,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故选:C.
15.解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc﹣c2,
∴图中空白部分的面积是:ab﹣(ac+bc﹣c2)=ab﹣bc﹣ac+c2.
故答案为:ab﹣bc﹣ac+c2.
16.解:∵AB=4,BC=2,
∴AC===2,
∵E为AC的中点,
∴AE=EC=,
∴S△AEF=S△ECF,
∵点C关于直线EF的对称点C′,
∴△CEF≌△C'EF,CE=C'E=,
∴S△CEF=S△C'EF,
∵△EFC′与△ACF重叠部分面积等于△ACF面积的,
∴S△EFG=S△AEF=S△CEF=S△C'EF,
∴AG=EG,FG=C'G,
在△C'EG和△FAG中,
,
∴△C'EG≌△FAG(SAS),
∴AF=C'E=,
∴BF=AB﹣AF=4﹣,
故答案为:=,4﹣.
17.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴AM=PE=BN,AE=MP=DF,MD=PF=NC,BE=PN=FC,
S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△EBP=S△DPF,且S△EBP+S△DPF=9,
∴EP×BE=PF×DF,且EP×BE+PF×DF=9,
∴EP×BE=PF×DF=
∵BE2+EP2=BP2=20,PF2+DF2=PD2=36,
∴BE+EP=,PF+DF=3
∴BE+EP+PF+DF=+3
∴AB+AD=+3
∴矩形ABCD的周长=2(AB+AD)=2+6
故答案为:2+6
18.解:过点O作OM⊥AB于点M,
∵四边形ABCD是矩形,
∴∠ADC=∠DAB=90°,OA=OB=OC=OD,
又∵DE平分∠ADC,
∴∠ADE=45°,
∴△DAE为等腰直角三角形,
∴AE=DA,
∵AD=6,AB=8,
∴AE=6,BE=2,
在Rt△DAB中,
AC===10,
∴OA=OB=5,
∵OM⊥AB,
∴AM=MB=4,
∴OM===3,
又∵ME=MB﹣EB=4﹣2=2,
在Rt△OME中,
OE===,
故答案为:.
19.解:过点C作AB的垂线垂足是E,如图所示:
∵将四根木条钉成的矩形木框变形为平行四边形木框ABCD的形状,并使其面积为矩形木框的,
∴BC=CE,
∵sin∠CBE==,
∴∠CBE=∠A=45°.
故答案为:45.
20.解:连接GH,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点G,H分别是AB,CD的中点,
∴BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=18,
当EF=GH=18时,平行四边形GFHE是矩形,
分两种情况:
①AE=CF=t,EF=24﹣2t=18,
解得:t=3;
②AE=CF=t,EF=24﹣2(24﹣t)=18,
解得:t=21;
综上所述:当t为3s或21s时,四边形EGFH为矩形;
故答案为:3或21.
21.解:∵四边形ABCD是矩形,
∴AC=BD,
∵矩形ABCD的对角线AC,BD的长度是关于x的方程x2﹣px+p+3=0的两个实数根,
∴Δ=p2﹣4×1×(p+3)=0,
解得:p1=6,p2=﹣2(不符合题意,舍去),
则方程为x2﹣6x+9=0,
即AC=BD=3,
由勾股定理得:AB2+BC2=AC2=9,
∵S=AC×BD,
∴S≤AC×BD=,
故答案为:.
22.解:∵过A,B间任意一点作AD的平行线,被每条小路截得的线段长都是2米,
∴S1=2b平方米;S2=2b平方米.
∴S1=S2.
故答案为:=.
23.解:仔细观察可看出,右下方的阶梯的水平方向的线段的和等于6厘米,垂直方向的线段的和等于8厘米.则其周长刚好等于矩形的周长=2×(8+6)=28厘米.
故答案为28.
24.解:∵四边形ABD是矩形,
∴AB=CD,AD=BC,∠A=∠D=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠DCE+∠DEC=90°.
∴∠AEF=∠DCE,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS).
∴AE=CD,AF=DE=2,
∴AD=AE+DE=AE+2,
∵矩形ABCD的周长为24,
∴2(AE+ED+CD)=24,
∴2(2AE+2)=24,
解得:CD=AE=5,
∴AD=7,
∴矩形ABCD的面积=AD×CD=7×5=35,
故答案为:35.
25.解:延长AP交CD于F,
∵∠APB=90°,
∴∠FPB=90°,
∴∠CPF+∠CPB=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=90°,BC=AD=3,
∴∠EAP+∠BAP=∠ABP+∠BAP=90°,
∴∠EAP=∠ABP,
∵CP=CB=3,
∴∠CPB=∠CBP,
∴∠CPF=∠ABP=∠EAP,
∵∠EPA=∠CPF,
∴∠EAP=∠APE,
∴AE=PE,
∵CD2+DE2=CE2,
∴42+(3﹣AE)2=(3+AE)2,
解得:AE=,故答案为:.
26.解:∵四边形ABCD是矩形,
∴O1A=O1C,O1B=O1D,AC=BD,
∴O1A=O1C=O1B=O1D,
∴=S△ABC=S矩形ABCD=×16cm2=4cm2,
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O1是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2××AO2×BO1=2×4cm2=8cm2,
∴△ABO2的面积是=2cm2,
同理平行四边形ABC2O2的面积是4cm2,
平行四边形ABC3O3的面积是2cm2,
平行四边形ABC4O4的面积是1cm2,
平行四边形ABC5D5的面积是cm2,
平行四边形ABC6O6的面积是cm2,
故答案为:.
27.解:连接DE,如图:
∵沿过A点的直线折叠,使得B点落在AD边上的点F处,
∴四边形ABEF为正方形,
∴∠EAD=45°,
由第二次折叠知,M点正好在∠NDG的平分线上,
∴DE平分∠GDC,
∴∠GDE=∠CDE,
∵DG为折痕,
∴∠DGE=90°=∠C,
而DE=DE,
∴Rt△DGE≌Rt△DCE(AAS),
∴DC=DG,
∵∠EAD=45°,∠DGA=90°,
∴△AGD为等腰直角三角形,
∴AD=DG=CD,
∴矩形ABCD长与宽的比值为,
故答案为.
28.解:(1)证明:连接DE,如图:
∵四边形ABCD为矩形,
∴∠C=90°,AD∥BC,
∴∠ADE=∠CED,
∵DF⊥AE,
∴∠DFE=90°,
∴∠DFE=∠C,
∵=λ=1,
∴AD=AE,
∴∠ADE=∠FED,
∴∠FED=∠CED,
在△DFE和△DCE中,
,
∴△DFE≌△DCE(AAS),
∴CE=FE;
29.解:(1)∠CGH=∠DFE,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴CG∥DF,∵GH∥EF,
∴∠AGC=∠AFD,∠AGH=∠AFE,
∵∠CGH=∠AGC+∠AGH,∠DFE=∠DFA+∠AFE,
∴∠CGH=∠DFE;
(2)①GH平分∠AGE;
理由如下:
∵GH∥EF,
∴∠AGH=∠AFE,∠HGE=∠GEF,
∵CE∥DF,
∴∠1=∠GEF,
∵∠1=∠GFE,
∴∠GFE=∠GEF,
∴∠AGH=∠EGH,
∴GH平分∠AGE;
②∵将一长方形纸片ABCD沿着EF折叠,
∴∠EFG=∠1,
∵∠DFG=52°,
∴∠EFG=64°,
∵GH∥EF,
∴∠AGH=∠AFE=64°,
∵∠EGF=∠DFG=52°,
∴∠HGE=64°.
30.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
又DE=BF,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)∵BD⊥AD,AB=5,AD=3,
∴BD==4,
连接AC交EF于O,
∴DO=BD=2,
∴AO==,
∵四边形AFCE是矩形,
∴AC=EF,AO=AC,EO=EF,
∴AO=EO=,
∴DE=EO﹣DO=﹣2.
二.矩形的判定
31.解:四边形ABCD为矩形.
理由:∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
故答案为:矩形.
32.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,AB∥EC,
∴四边形ABEC是平行四边形;
(2)∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠ADC,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
33.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
34.证明:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵,
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴AD=CN;
②∵∠BAN=90度,四边形ADCN是平行四边形,
∴四边形ADCN是矩形.
35.证明:(1)连接DF.
∵D是BC边上的中点,
∴BD=DC,
∵AF∥BC,且AF=BD,
∴AF∥DC,且AF=DC,
∴四边形ACDF是平行四边形,
∴AE=ED;
(2)四边形AFBD是矩形,
理由如下:
由(1)得,四边形ACDF是平行四边形,
∵AB=AC,BD=DC.
∴AD⊥BC,即∠ADB=90°.
∴平行四边形AFBD是矩形.
36.(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=×180°=90°.
即∠ECF=90°,
∴四边形AECF是矩形.
37.(1)证明:在△ADF和△CDE中,
∵AF∥BE,
∴∠FAD=∠ECD.
又∵D是AC的中点,
∴AD=CD.
∵∠ADF=∠CDE,
∴△ADF≌△CDE.
∴AF=CE.
(2)解:若AC=EF,则四边形AFCE是矩形.
证明:由(1)知:AF=CE,AF∥CE,
∴四边形AFCE是平行四边形.
又∵AC=EF,
∴平行四边形AFCE是矩形.
三.矩形的判定与性质
38.解:∵Rt△ABC中,∠A=90°,AC=8,BA=6,
∴BC=10,
连接AD,
∵DE⊥AB,DF⊥AC,
∴四边形EAFD是矩形,
∴EF=AD,
当AD最小时,则EF最小,根据垂线段最短可知当AD⊥BC时,则AD最小,
∴EF=AD==,
故选:B.
39.解:(1)当时间t=7秒时,四边形BPDQ为矩形.
理由如下:当t=7秒时,PA=QC=7,
∵AC=6,
∴CP=AQ=1
∴PQ=BD=8
∵四边形ABCD为平行四边形,BD=8
∴AO=CO=3
∴BO=DO=4
∴OQ=OP=4
∴四边形BPDQ为平形四边形,
∵PQ=BD=8
∴四边形BPDQ为矩形,
(2)由(1)得BO=4,CQ=7,
∵BC⊥AC
∴∠BCA=90°
BC2+CQ2=BQ2
∴BQ=.
40.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴ BECD是矩形;
(2)如图,
∵CD=3,
∴AB=BE=3.
∵AD=6,∠ABD=90°,
∴BD===3,
∴CE=3,
∴AC===3.
41.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
解得:x=2±,
∵0<x<2,
∴x=2﹣.
42.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:作OF⊥BC于F,如图所示.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积= EC OF=1.
43.(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,AD∥BC,
∴∠A+∠D=180°,
∵AN=DM,
∴AM=DN,
在△ABM和△DCN中,,
∴△ABM≌△DCN(SSS),
∴∠A=∠D,
∵∠A+∠D=180°,
∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
(2)解:∴△ABM≌△DCN,
∴∠AMB=∠DNC,
∵AD∥BC,
∴∠AMB=∠OBC,∠DNC=∠OCB,
∴∠OBC=∠OCB,
∵∠BOC=90°,
∴△OBC是等腰直角三角形,
∴AMB=∠OBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵AM MD=12,AN=DM,
∴AM(AM﹣1)=12,
解得:AM=4,或AM=﹣3(舍去),
∴AB=AM=4,MD=3,
∴AD=AM+MD=7,
∴矩形ABCD的面积=AD×AB=7×4=28.
44.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AE⊥BD于点E,DF⊥AC于点F,
∴∠AEO=∠DFO=90°,
在△AEO和△DFO中,,
∴△AEO≌△DFO(AAS),
∴OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:由(1)得:四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,OA=OB,
∴∠OAB=∠OBA,
∵∠BAE:∠EAD=2:3,
∴∠BAE=36°,
∴∠OBA=∠OAB=90°﹣36°=54°,
∴∠EAO=∠OAB﹣∠BAE=54°﹣36°=18°
一.矩形的性质
1.一次数学课上,老师请同学们在一张长为18厘米,宽为16厘米的长方形纸板上,剪下一个腰长为10厘米的等腰三角形,且要求等腰三角形的一个顶点与长方形的一个顶点重合,其它两个顶点在长方形的边上,则剪下的等腰三角形的面积为( )平方厘米.
A.50或60 B.40或50或80 C.30或40或50 D.30或50或80
2.如图,在矩形ABCD中,对角线AC,BD相交于点O,DE⊥AC于点E,∠EDC:∠EDA=1:2,且AC=8,则EC的长度为( )
A.2 B.2 C.4 D.
3.如图,在矩形ABCD中,点F为边AD上一点,过F作EF∥AB交边BC于点E,P为边AB上一点,PH⊥DE交线段DE于H,交线段EF于Q,连接DQ.当AF=AB时,要求阴影部分的面积,只需知道下列某条线段的长,该线段是( )
A.EF B.DE C.PH D.PE
4.如图,E、F分别是矩形ABCD边上的两点,设∠ADE=α,∠EDF=β,∠FDC=γ,若∠AED=α+β,下列结论正确的是( )
A.α=β B.α=γ C.α+β+2γ=90° D.2α+γ=90°
5.在矩形ABCD中,点A关于∠B的角平分线的对称点为E,点E关于∠C的角平分线的对称点为F.若AD=,AB=1,则AF2=( )
A.8﹣4 B.10﹣4 C.8+4 D.10+4
6.如图,在矩形ABCD中,AB=4,AD=6,点F是AB的中点,E为BC边上一点,且EF⊥ED,连接DF,M为DF的中点,连接MA,ME.若AM⊥ME,则AE的长为( )
A.5 B. C. D.
7.如图,在矩形ABCD中,对角线AC、BD交于点O,∠BAD的平分线交BC于E,若∠EAC=15°,则∠COE=( )
A.45° B.60° C.75° D.30°
8.已知点P是矩形ABCD内一点,连接AP、BP、CP、DP,若S△ABP+S△CDP=S△ADP+S△BCP,则关于点P的位置,正确的说法是( )
A.一定是对角线交点 B.一定在对角线上
C.一定在对边中点的连线上 D.可以是任意位置
9.如图是一块矩形ABCD的场地,长AB=102,宽AD=51,从A、B两处入口的中路宽都为1,两小路汇合处路宽为2,其余部分种植草坪,则草坪面积为( )
A.5050 B.4900 C.5000 D.4998
10.如图,矩形ABCD中,对角线AC,BD交于点O,点E是边AB上一点,且OE⊥AC.设∠AOD=α,∠AEO=β,则α与β间的关系正确的是( )
A.α=β B.α+β=180° C.2α+β=180° D.α+2β=180°
11.如图,矩形ABCD中,E,F是CD上的两个点,EG⊥AC,FH⊥AC,垂足分别为G,H,若AD=2,DE=1,CF=2,且AG=CH,则EG+FH=( )
A.+1 B. C.3 D.
12.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC于点E,DF平分∠ADC,交EB的延长线于点F,BC=6,CD=3,则为( )
A. B. C. D.
13.如图所示,P是矩形ABCD内的任意一点,连接PA,PB,PC,PD,得到△PAB,△PBC,△PCD,△PDA,设它们的面积分别是S1,S2,S3,S4,给出如下结论:①S1+S4=S2+S3;②S2+S4=S1+S3;③若S3=2S1,则S4=2S2;④若S1=S2,则S3=S4,其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
14.如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
15.矩形ABCD中,横向阴影部分是长方形,另一部分是平行四边形,依照图中标注的数据,图中空白部分的面积为 .
16.如图,矩形ABCD中,,连结对角线AC,E为AC的中点,F为边AB上的动点,连结EF,作点C关于直线EF的对称点C′,连结C′E,C′F,CF,若△EFC′与△ACF重叠部分面积等于△ACF面积的,则AG EG(填“>”、“=”或“<”),BF= .
17.如图,在矩形ABCD中,点P在对角线AC上,过点P作EF∥BC,分别交AB,CD于点E,F,连接PB,PD.若PB=2,PD=6,图中阴影部分的面积为9,则矩形ABCD的周长为 .
18.如图,在矩形ABCD中对角线AC,BD交于点O,DE平分∠ADC交AB于点E,连接OE,若AD=6,AB=8,则OE= .
19.将四根木条钉成的长方形木框变形为平行四边形ABCD的形状,并使其面积为长方形面积的倍(木条宽度忽略不计),则这个平行四边形的最小内角为 度.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,E,F是对角线AC上的两个动点,分别从A,C处同时出发相向而行,到C,A时停止运动.若两动点的速度均为1cm/s,AB=14cm,BC=18cm,AC=24cm,经t秒后,四边形GFHE为矩形,则此时t的值为 .
21.已知矩形ABCD的对角线AC,BD的长度是关于x的方程x2﹣px+p+3=0的两个实数根,则此矩形面积的最大值是 .
22.如图,一块长为a米,宽为b米的矩形土地被踩出两条小路(过A,B间任意一点作AD的平行线,被每条小路截得的线段长都是2米).若小路①,②的面积分别为S1,S2,则S1,S2的大小关系是s1 s2.
23.如图所示,图形的周长为 厘米.
24.如图,在矩形ABCD中,E,F分别为AD,AB上一点,且EF=EC,EF⊥EC,若DE=2,矩形ABCD的周长为24,则矩形ABCD的面积为 .
25.如图,长方形ABCD中,AB=4,AD=3,长方形内有一个点P,连接AP,BP,CP,已知∠APB=90°,CP=CB,延长CP交AD于点E,则AE= .
26.如图,矩形ABCD的面积为16cm2,它的两条对角线交于点O1,以AB、AO1为邻边作 ABC1O1,设 ABC1O1的对角线交于点O2,同样以AB、AO2为邻边作 ABC2O2,…,依此类推,则 ABC6O6的面积为 cm2.
27.小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,求矩形ABCD长与宽的比值.
28.如图,在矩形ABCD中,E是BC上一点,DF⊥AE于点F,设=λ(λ>0).若λ=1,求证:CE=FE;
29.如图,将一长方形纸片ABCD沿着EF折叠,已知AF∥BE,DF∥CE,CE交AF于点G,过点G作GH∥EF,交线段BE于点H.
(1)判断∠CGH与∠DFE是否相等,并说明理由;
(2)①判断GH是否平分∠AGE,并说明理由;
②若∠DFA=52°,求∠HGE的度数.
30.如图,在 ABCD中,点E,F是直线BD上的两点,DE=BF.
(1)求证:四边形AFCE是平行四边形.
(2)若BD⊥AD,AB=5,AD=3,四边形AFCE是矩形,求DE的长.
二.矩形的判定
31.已知Rt△ABC,∠ABC=90°,小明按如下步骤作图,①以A为圆心,BC长为半径作弧,以C为圆心,AB长为半径作弧,两弧相交于点D;②连接DA,DC,则四边形ABCD为 .
32.如图,将 ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:四边形ABEC是平行四边形;
(2)若∠AFC=2∠ADC,求证:四边形ABEC是矩形.
33.如图,在四边形ABCD中,AC、BD相交于点O,AD∥BC,∠ADC=∠ABC,OA=OB.
(1)如图1,求证:四边形ABCD为矩形;
(2)如图2,P是AD边上任意一点,PE⊥BD,PF⊥AC,E、F分别是垂足,若AD=12,AB=5,求PE+PF的值.
34.已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
35.如图,在△ABC中,D是BC边上的中点,过A点作AF∥BC,且AF=BD,连接CF交AD于点E.
(1)求证:AE=ED;
(2)若AB=AC,试判断四边形AFBD形状,并说明理由.
36.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
37.已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE,CF.
(1)求证:AF=CE;
(2)若AC=EF,试判断四边形AFCE是什么样的四边形,并证明你的结论.
三.矩形的判定与性质
38.如图,在△ABC中,∠A=90°,AC=8,AB=6,点D是BC边上的动点(不与B,C重合)过点D作DE⊥AB于点E,作DF⊥AC于点F,则EF的最小值是( )
A.3 B. C.5 D.
39.如图,平行四边形ABCD中,AC=6,BD=8,点P从点A出发以每秒1cm的速度沿射线AC移动,点Q从点C出发以每秒1cm的速度沿射线CA移动.
(1)经过几秒,以P,Q,B,D为顶点的四边形为矩形?
(2)若BC⊥AC垂足为C,求(1)中矩形边BQ的长.
40.如图,已知 ABCD,延长AB到E,使BE=AB,连接BD,ED,EC,若ED=AD.
(1)求证:四边形BECD是矩形;
(2)连接AC,若AD=6,CD=3,求AC的长.
41.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC上.
(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.
(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x的值.
42.如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
43.如图,在平行四边形ABCD中,点M,N是AD边上的点,BM,CN交于点O,AN=DM,BM=CN.
(1)求证:平行四边形ABCD是矩形.
(2)若∠BOC=90°,MN=1,AM MD=12,求矩形ABCD的面积.
44.如图,平行四边形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F,且AE=DF.
(1)求证:四边形ABCD是矩形.
(2)若∠BAE:∠EAD=2:3,求∠EAO的度数.
参考答案
一.矩形的性质
1.解:分三种情况讨论:
①如图1所示:
BE=BF=10,
等腰三角形的面积=10×10÷2=50(cm2);
②如图2所示:
BE=16﹣10=6(cm),
BF==8(cm),
等腰三角形的面积=10×8÷2=40(cm2);
③如图3所示:
DE=18﹣10=8(cm),
DF==6(cm),
等腰三角形的面积=10×6÷2=30(cm2).
故选:C.
2.解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=8,OA=OC=AC=4,OB=OD=BD=4,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:2,∠EDC+∠EDA=90°,
∴∠EDC=30°,∠EDA=60°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DAC=30°,
∴DC=AC=4,
∴EC=DC=2,
故选:B.
3.解:过点P作PM⊥EF于点M,如图:
∵四边形ABCD为矩形,
∴AB∥DC,AD∥BC,∠C=90°,
∵EF∥AB,
∴EF∥DC,
∴∠EDC=∠DEF,
∵PH⊥DE,PM⊥EF,
∴∠PMQ=∠EHQ=90°,
又∵∠PQM=∠EQH,
∴∠QPM=∠DEF=∠EDC,
在△PMQ和△DCE中,
,
∴△PMQ≌△DCE(ASA),
∴PQ=DE,
∴阴影部分的面积=S△PDE﹣S△QED=×DE×PH﹣DE×QH=DE2,
∴故选:B.
4.解:∵四边形ABCD是矩形,
∴∠A=∠ADC=90°,
∵∠ADE=α,∠EDF=β,∠FDC=γ,
∴α+β+γ=90°,
∵∠AED+α=90°,∠AED=α+β,
∴2α+β=90°,
∴α+β+γ=2α+β,
∴α=γ,
故选:B.
5.解:∵四边形ABCD是矩形,
∴AB=CD=1,BC=AD=,
∵点A关于∠B的角平分线的对称点为E,点E关于∠C的角平分线的对称点为F,
∴AB=BE=1,CE=CF=﹣1,
∴DF=CD﹣CF=2﹣,
∴AF2=AD2+DF2=3+7﹣4=10﹣4,
故选:B.
6.解:∵四边形ABCD是矩形,
∴∠DAF=90°,
∵EF⊥DE,
∴∠DEF=90°,
∵FM=DM,
∴AM=EM=DF=×=,
∵AM⊥ME,
∴∠AME=90°,
∴AE===2,
故选:B.
7.解:∵四边形ABCD是矩形,
∴AO=BO,∠BAD=∠ABE=90°,
∵AE平分∠BAD,
∴∠BAE=45°,
又∵∠CAE=15°,
∴∠BAO=45°+15°=60°,
∴△ABO是等边三角形,
∴AB=BO,
又∵∠BAE=45°=∠AEB,
∴AB=EB,
∴BO=BE,
∴∠BOE==75°,
∴∠COE=180°﹣∠AOB﹣∠BOE=180°﹣60°﹣75°=45°,
故选:A.
8.解:∵四边形ABCD是矩形,
∴AD=BC,AB=CD,
作PE⊥AD于E,延长EP交BC于F,如图所示:
则PF⊥BC,EF=AB,
∵△ADP的面积+△BCP的面积=AD PE+BC PF=BC(PE+PF)=BC EF=BC AB,
∴△ADP的面积+△BCP的面积=矩形ABCD的面积,
同理:△ABP的面积+△CDP的面积=矩形ABCD的面积,
∴△ADP的面积+△BCP的面积=△ABP的面积+△CDP的面积;
故选:D.
9.解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:102﹣2=100,宽为51﹣1=50.所以草坪的面积应该是长×宽=100×50=5000.
故选:C.
10.解:∵四边形ABCD是矩形,
∴OA=OD,
∴∠OAD=∠ODA,
∵∠AOD=α,
∴∠OAD=(180°﹣α),
∵OE⊥AC,
∴∠AOE=90°,
∵∠AEO=β,∠DAE=90°,
∴∠OAD=∠AEO,
∴(180°﹣α)=β,
∴α+2β=180°.故选:D.
11.解:过点E作EM⊥AB于M,延长EG交AB于Q,则△EQM是直角三角形.
∵EG⊥AC,FH⊥AC,
∴∠CHF=∠AGQ=90°,
∵矩形ABCD中,CD∥AB,
∴∠FCH=∠QAG,
在△FCH和△QAG中,
,
∴△FCH≌△QAG(ASA),
∴AQ=CF=2,FH=QG,
∵∠D=∠DAM=∠AME=90°,
∴四边形ADEM是矩形,
∴AM=DE=1,EM=AD=2,
∴MQ=2﹣1=1,
∴Rt△EMQ中,EQ===,
即EG+QG=EG+FH=.故选:B.
12.证明:∵四边形ABCD为矩形,
∴AC=BD,∠ADC=90°,OA=OD,
∴∠COD=2∠ADO,
又∵BE⊥AC,
∴∠EOB+∠EBO=90°,
∵∠EBO=∠BDF+∠F,
∴2∠ADO+∠BDF+∠F=90°,
又∵DF平分∠ADC,
∴∠ADO+∠BDF=∠ADC=45°,
∴2∠ADO+∠BDF+∠F=45°+∠ADO+∠F=90°,
∴∠ADO+∠F=45°,
又∵∠BDF+∠ADO=45°,
∴∠BDF=∠F,
∴BF=BD,
∴AC=BF,
∵BC=6,CD=3,
∴AD=6,
∴BF=AC==3,
∵S△ABC=AC BE=AB BC,
∴BE=,
∴==,
故选:C.
13.解:如图,过点P分别作PF⊥AD于点F,PE⊥AB于点E,
∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3=矩形ABCD面积;
同理可得出S2+S4=矩形ABCD面积;
∴②S2+S4=S1+S3正确;
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4.
但P是矩形ABCD内的任意一点,所以该等式不一定成立.
故①不一定正确;
③若S3=2S1,只能得出△APB与△PDC高度之比,S4不一定等于2S2;
故此选项错误;
∵S2+S4=S1+S3;若S1=S2,则S3=S4,
∴④正确.故选:B.
14.解:∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=AB,
∵AD=AB,
∴AE=AD,
在△ABE和△AHD中,
,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB=(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE﹣AH=BC﹣CD,
∴BC﹣CF=BC﹣(CD﹣DF)=BC﹣(CD﹣HE)=(BC﹣CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故选:C.
15.解:∵矩形ABCD的面积是ab,
阴影部分的面积是:ac+bc﹣c2,
∴图中空白部分的面积是:ab﹣(ac+bc﹣c2)=ab﹣bc﹣ac+c2.
故答案为:ab﹣bc﹣ac+c2.
16.解:∵AB=4,BC=2,
∴AC===2,
∵E为AC的中点,
∴AE=EC=,
∴S△AEF=S△ECF,
∵点C关于直线EF的对称点C′,
∴△CEF≌△C'EF,CE=C'E=,
∴S△CEF=S△C'EF,
∵△EFC′与△ACF重叠部分面积等于△ACF面积的,
∴S△EFG=S△AEF=S△CEF=S△C'EF,
∴AG=EG,FG=C'G,
在△C'EG和△FAG中,
,
∴△C'EG≌△FAG(SAS),
∴AF=C'E=,
∴BF=AB﹣AF=4﹣,
故答案为:=,4﹣.
17.解:作PM⊥AD于M,交BC于N.
则有四边形AEPM,四边形DFPM,四边形CFPN,四边形BEPN都是矩形,
∴AM=PE=BN,AE=MP=DF,MD=PF=NC,BE=PN=FC,
S△ADC=S△ABC,S△AMP=S△AEP,S△PBE=S△PBN,S△PFD=S△PDM,S△PFC=S△PCN,
∴S△EBP=S△DPF,且S△EBP+S△DPF=9,
∴EP×BE=PF×DF,且EP×BE+PF×DF=9,
∴EP×BE=PF×DF=
∵BE2+EP2=BP2=20,PF2+DF2=PD2=36,
∴BE+EP=,PF+DF=3
∴BE+EP+PF+DF=+3
∴AB+AD=+3
∴矩形ABCD的周长=2(AB+AD)=2+6
故答案为:2+6
18.解:过点O作OM⊥AB于点M,
∵四边形ABCD是矩形,
∴∠ADC=∠DAB=90°,OA=OB=OC=OD,
又∵DE平分∠ADC,
∴∠ADE=45°,
∴△DAE为等腰直角三角形,
∴AE=DA,
∵AD=6,AB=8,
∴AE=6,BE=2,
在Rt△DAB中,
AC===10,
∴OA=OB=5,
∵OM⊥AB,
∴AM=MB=4,
∴OM===3,
又∵ME=MB﹣EB=4﹣2=2,
在Rt△OME中,
OE===,
故答案为:.
19.解:过点C作AB的垂线垂足是E,如图所示:
∵将四根木条钉成的矩形木框变形为平行四边形木框ABCD的形状,并使其面积为矩形木框的,
∴BC=CE,
∵sin∠CBE==,
∴∠CBE=∠A=45°.
故答案为:45.
20.解:连接GH,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵点G,H分别是AB,CD的中点,
∴BG=CH,BG∥CH,
∴四边形BCHG是平行四边形,
∴GH=BC=18,
当EF=GH=18时,平行四边形GFHE是矩形,
分两种情况:
①AE=CF=t,EF=24﹣2t=18,
解得:t=3;
②AE=CF=t,EF=24﹣2(24﹣t)=18,
解得:t=21;
综上所述:当t为3s或21s时,四边形EGFH为矩形;
故答案为:3或21.
21.解:∵四边形ABCD是矩形,
∴AC=BD,
∵矩形ABCD的对角线AC,BD的长度是关于x的方程x2﹣px+p+3=0的两个实数根,
∴Δ=p2﹣4×1×(p+3)=0,
解得:p1=6,p2=﹣2(不符合题意,舍去),
则方程为x2﹣6x+9=0,
即AC=BD=3,
由勾股定理得:AB2+BC2=AC2=9,
∵S=AC×BD,
∴S≤AC×BD=,
故答案为:.
22.解:∵过A,B间任意一点作AD的平行线,被每条小路截得的线段长都是2米,
∴S1=2b平方米;S2=2b平方米.
∴S1=S2.
故答案为:=.
23.解:仔细观察可看出,右下方的阶梯的水平方向的线段的和等于6厘米,垂直方向的线段的和等于8厘米.则其周长刚好等于矩形的周长=2×(8+6)=28厘米.
故答案为28.
24.解:∵四边形ABD是矩形,
∴AB=CD,AD=BC,∠A=∠D=90°,
∵EF⊥EC,
∴∠FEC=90°,
∴∠AEF+∠DEC=90°,
∵∠DCE+∠DEC=90°.
∴∠AEF=∠DCE,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS).
∴AE=CD,AF=DE=2,
∴AD=AE+DE=AE+2,
∵矩形ABCD的周长为24,
∴2(AE+ED+CD)=24,
∴2(2AE+2)=24,
解得:CD=AE=5,
∴AD=7,
∴矩形ABCD的面积=AD×CD=7×5=35,
故答案为:35.
25.解:延长AP交CD于F,
∵∠APB=90°,
∴∠FPB=90°,
∴∠CPF+∠CPB=90°,
∵四边形ABCD是矩形,
∴∠DAB=∠ABC=90°,BC=AD=3,
∴∠EAP+∠BAP=∠ABP+∠BAP=90°,
∴∠EAP=∠ABP,
∵CP=CB=3,
∴∠CPB=∠CBP,
∴∠CPF=∠ABP=∠EAP,
∵∠EPA=∠CPF,
∴∠EAP=∠APE,
∴AE=PE,
∵CD2+DE2=CE2,
∴42+(3﹣AE)2=(3+AE)2,
解得:AE=,故答案为:.
26.解:∵四边形ABCD是矩形,
∴O1A=O1C,O1B=O1D,AC=BD,
∴O1A=O1C=O1B=O1D,
∴=S△ABC=S矩形ABCD=×16cm2=4cm2,
∵四边形ABC1O1是平行四边形,O1A=O1B,
∴四边形ABC1O1是菱形,
∴AC1=2O2A,O1B=2O1O2=2O2B,AC1⊥BO1,
∴平行四边形ABC1O1的面积是AC1×BO1=×2AO2×BO1=2××AO2×BO1=2×4cm2=8cm2,
∴△ABO2的面积是=2cm2,
同理平行四边形ABC2O2的面积是4cm2,
平行四边形ABC3O3的面积是2cm2,
平行四边形ABC4O4的面积是1cm2,
平行四边形ABC5D5的面积是cm2,
平行四边形ABC6O6的面积是cm2,
故答案为:.
27.解:连接DE,如图:
∵沿过A点的直线折叠,使得B点落在AD边上的点F处,
∴四边形ABEF为正方形,
∴∠EAD=45°,
由第二次折叠知,M点正好在∠NDG的平分线上,
∴DE平分∠GDC,
∴∠GDE=∠CDE,
∵DG为折痕,
∴∠DGE=90°=∠C,
而DE=DE,
∴Rt△DGE≌Rt△DCE(AAS),
∴DC=DG,
∵∠EAD=45°,∠DGA=90°,
∴△AGD为等腰直角三角形,
∴AD=DG=CD,
∴矩形ABCD长与宽的比值为,
故答案为.
28.解:(1)证明:连接DE,如图:
∵四边形ABCD为矩形,
∴∠C=90°,AD∥BC,
∴∠ADE=∠CED,
∵DF⊥AE,
∴∠DFE=90°,
∴∠DFE=∠C,
∵=λ=1,
∴AD=AE,
∴∠ADE=∠FED,
∴∠FED=∠CED,
在△DFE和△DCE中,
,
∴△DFE≌△DCE(AAS),
∴CE=FE;
29.解:(1)∠CGH=∠DFE,
理由:∵四边形ABCD是矩形,
∴AD∥BC,
∴CG∥DF,∵GH∥EF,
∴∠AGC=∠AFD,∠AGH=∠AFE,
∵∠CGH=∠AGC+∠AGH,∠DFE=∠DFA+∠AFE,
∴∠CGH=∠DFE;
(2)①GH平分∠AGE;
理由如下:
∵GH∥EF,
∴∠AGH=∠AFE,∠HGE=∠GEF,
∵CE∥DF,
∴∠1=∠GEF,
∵∠1=∠GFE,
∴∠GFE=∠GEF,
∴∠AGH=∠EGH,
∴GH平分∠AGE;
②∵将一长方形纸片ABCD沿着EF折叠,
∴∠EFG=∠1,
∵∠DFG=52°,
∴∠EFG=64°,
∵GH∥EF,
∴∠AGH=∠AFE=64°,
∵∠EGF=∠DFG=52°,
∴∠HGE=64°.
30.证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∴∠ADB=∠CBD.
∴∠ADE=∠CBF.
又DE=BF,
∴△ADE≌△CBF(SAS).
∴AE=CF,∠AED=∠CBF.
∴AE∥CF,
∴四边形AFCE是平行四边形;
(2)∵BD⊥AD,AB=5,AD=3,
∴BD==4,
连接AC交EF于O,
∴DO=BD=2,
∴AO==,
∵四边形AFCE是矩形,
∴AC=EF,AO=AC,EO=EF,
∴AO=EO=,
∴DE=EO﹣DO=﹣2.
二.矩形的判定
31.解:四边形ABCD为矩形.
理由:∵AD=BC,AB=DC,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形.
故答案为:矩形.
32.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵CE=DC,
∴AB=EC,AB∥EC,
∴四边形ABEC是平行四边形;
(2)∵由(1)知,四边形ABEC是平行四边形,
∴FA=FE,FB=FC.
∵四边形ABCD是平行四边形,
∴∠ABC=∠D.
又∵∠AFC=2∠ADC,
∴∠AFC=2∠ABC.
∵∠AFC=∠ABC+∠BAF,
∴∠ABC=∠BAF,
∴FA=FB,
∴FA=FE=FB=FC,
∴AE=BC,
∴四边形ABEC是矩形.
33.证明:(1)∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形;
(2)如图,连接OP,
∵AD=12,AB=5,
∴BD===13,
∴BO=OD=AO=CO=,
∵S△AOD=S矩形ABCD=×12×5=15,
∴S△AOP+S△POD=15,
∴××FP+××EP=15,
∴PE+PF=.
34.证明:①∵CN∥AB,
∴∠DAC=∠NCA,
在△AMD和△CMN中,
∵,
∴△AMD≌△CMN(ASA),
∴AD=CN,
又∵AD∥CN,
∴四边形ADCN是平行四边形,
∴AD=CN;
②∵∠BAN=90度,四边形ADCN是平行四边形,
∴四边形ADCN是矩形.
35.证明:(1)连接DF.
∵D是BC边上的中点,
∴BD=DC,
∵AF∥BC,且AF=BD,
∴AF∥DC,且AF=DC,
∴四边形ACDF是平行四边形,
∴AE=ED;
(2)四边形AFBD是矩形,
理由如下:
由(1)得,四边形ACDF是平行四边形,
∵AB=AC,BD=DC.
∴AD⊥BC,即∠ADB=90°.
∴平行四边形AFBD是矩形.
36.(1)证明:∵CE平分∠ACB,
∴∠1=∠2,
又∵MN∥BC,
∴∠1=∠3,
∴∠3=∠2,
∴EO=CO,
同理,FO=CO,
∴EO=FO.
(2)解:当点O运动到AC的中点时,四边形AECF是矩形.
理由:
∵EO=FO,点O是AC的中点.
∴四边形AECF是平行四边形,
∵CF平分∠BCA的外角,
∴∠4=∠5,
又∵∠1=∠2,
∴∠2+∠4=×180°=90°.
即∠ECF=90°,
∴四边形AECF是矩形.
37.(1)证明:在△ADF和△CDE中,
∵AF∥BE,
∴∠FAD=∠ECD.
又∵D是AC的中点,
∴AD=CD.
∵∠ADF=∠CDE,
∴△ADF≌△CDE.
∴AF=CE.
(2)解:若AC=EF,则四边形AFCE是矩形.
证明:由(1)知:AF=CE,AF∥CE,
∴四边形AFCE是平行四边形.
又∵AC=EF,
∴平行四边形AFCE是矩形.
三.矩形的判定与性质
38.解:∵Rt△ABC中,∠A=90°,AC=8,BA=6,
∴BC=10,
连接AD,
∵DE⊥AB,DF⊥AC,
∴四边形EAFD是矩形,
∴EF=AD,
当AD最小时,则EF最小,根据垂线段最短可知当AD⊥BC时,则AD最小,
∴EF=AD==,
故选:B.
39.解:(1)当时间t=7秒时,四边形BPDQ为矩形.
理由如下:当t=7秒时,PA=QC=7,
∵AC=6,
∴CP=AQ=1
∴PQ=BD=8
∵四边形ABCD为平行四边形,BD=8
∴AO=CO=3
∴BO=DO=4
∴OQ=OP=4
∴四边形BPDQ为平形四边形,
∵PQ=BD=8
∴四边形BPDQ为矩形,
(2)由(1)得BO=4,CQ=7,
∵BC⊥AC
∴∠BCA=90°
BC2+CQ2=BQ2
∴BQ=.
40.证明:(1)∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵BE=AB,
∴BE=CD,
∴四边形BECD是平行四边形,
∵AD=BC,AD=DE,
∴BC=DE,
∴ BECD是矩形;
(2)如图,
∵CD=3,
∴AB=BE=3.
∵AD=6,∠ABD=90°,
∴BD===3,
∴CE=3,
∴AC===3.
41.(1)证明:连接MN,如图1所示:
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠B=90°,
∴∠EAM=∠FCN,AC===5,
∵M,N分别是AD,BC的中点,
∴AM=DM=BN=CN,AM∥BN,
∴四边形ABNM是平行四边形,
又∵∠B=90°,
∴四边形ABNM是矩形,
∴MN=AB=3,
在△AME和△CNF中,,
∴△AME≌△CNF(SAS),
∴EM=FN,∠AEM=∠CFN,
∴∠MEF=∠NFE,
∴EM∥FN,
∴四边形EMFN是平行四边形,
又∵AE=CF=1,
∴EF=AC﹣AE﹣CF=3,
∴MN=EF,
∴四边形EMFN为矩形.
(2)解:连接MN,作MH⊥BC于H,如图2所示:
则四边形ABHM是矩形,
∴MH=AB=3,BH=AM=x,
∴HN=BC﹣BH﹣CN=4﹣2x,
∵四边形EMFN为矩形,AE=CF=0.5,
∴MN=EF=AC﹣AE﹣CF=4,
在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,
解得:x=2±,
∵0<x<2,
∴x=2﹣.
42.(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:作OF⊥BC于F,如图所示.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积= EC OF=1.
43.(1)证明:∵四边形ABCD是平行四边形,
∴AB=DC,AB∥DC,AD∥BC,
∴∠A+∠D=180°,
∵AN=DM,
∴AM=DN,
在△ABM和△DCN中,,
∴△ABM≌△DCN(SSS),
∴∠A=∠D,
∵∠A+∠D=180°,
∴∠A=∠D=90°,
∴平行四边形ABCD是矩形.
(2)解:∴△ABM≌△DCN,
∴∠AMB=∠DNC,
∵AD∥BC,
∴∠AMB=∠OBC,∠DNC=∠OCB,
∴∠OBC=∠OCB,
∵∠BOC=90°,
∴△OBC是等腰直角三角形,
∴AMB=∠OBC=45°,
∴△ABM是等腰直角三角形,
∴AB=AM,
∵AM MD=12,AN=DM,
∴AM(AM﹣1)=12,
解得:AM=4,或AM=﹣3(舍去),
∴AB=AM=4,MD=3,
∴AD=AM+MD=7,
∴矩形ABCD的面积=AD×AB=7×4=28.
44.(1)证明:∵四边形ABCD是平行四边形,
∴OA=OC=AC,OB=OD=BD,
∵AE⊥BD于点E,DF⊥AC于点F,
∴∠AEO=∠DFO=90°,
在△AEO和△DFO中,,
∴△AEO≌△DFO(AAS),
∴OA=OD,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:由(1)得:四边形ABCD是矩形,
∴∠ABC=∠BAD=90°,OA=OB,
∴∠OAB=∠OBA,
∵∠BAE:∠EAD=2:3,
∴∠BAE=36°,
∴∠OBA=∠OAB=90°﹣36°=54°,
∴∠EAO=∠OAB﹣∠BAE=54°﹣36°=18°
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
