2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理同步练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学下册8.5平行线的性质定理同步练习题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 332.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 10:32:25 | ||
图片预览



文档简介
2021-2022学年鲁教版七年级数学下册《8-5平行线的性质定理》同步练习题(附答案)
1.如图,已知AB⊥AC,DE⊥AC,∠B=∠D.试说明:AD∥BC.
在下列解答中,填上适当的理由或数学式.
解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴ =∠DEC( ).
又∵∠B=∠D(已知),
∴∠D= (等量代换),
∴AD∥BC( ).
2.请补全证明过程及推理依据.
已知:如图,BC∥ED,BD平分∠ABC,EF平分∠AED.
求证:BD∥EF.
证明:∵BD平分∠ABC,EF平分∠AED,
∴∠1=∠AED,∠2=∠ABC( ).
∵BC∥ED,
∴∠AED= ( )
∴∠AED=∠ABC.
∴∠1=∠2( ).
∴BD∥EF( ).
3.如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于点O.
(1)若∠AMF=52°,∠CNE=38°,求∠MEN、∠MFN的度数;
(2)若2∠MFN﹣∠MEN=45°,求出∠AMF的度数;
(3)探究∠MEN、∠MFN与∠MON之间存在怎样的数量关系.(直接写出结果)
4.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,连接PM、PN、PQ,PQ平分∠MPN,如图①.
(1)若∠PMA=α、∠PQC=β,求∠NPQ的度数(用含α,β的式子表示);
(2)过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F,如图②,请你判断EF与PQ的位置关系,并说明理由;
(3)在(2)的条件下,连接EN,如图③,若∠NEF=∠PMA,求证:NE平分∠PNQ.
5.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( ),
∴∠3+∠ACB=180°,( ),
∴∠ACB= °,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( ).
6.完成下列推理过程.
(1)如图,已知AB∥CD,∠B+∠D=180°.
求证:BC∥DE.
证明:∵AB∥CD(已知),
∴∠ =∠ ( ).
∵∠B+∠D=180°(已知),
∴∠ +∠D=180°(等量代换),
∴BC∥DE( )
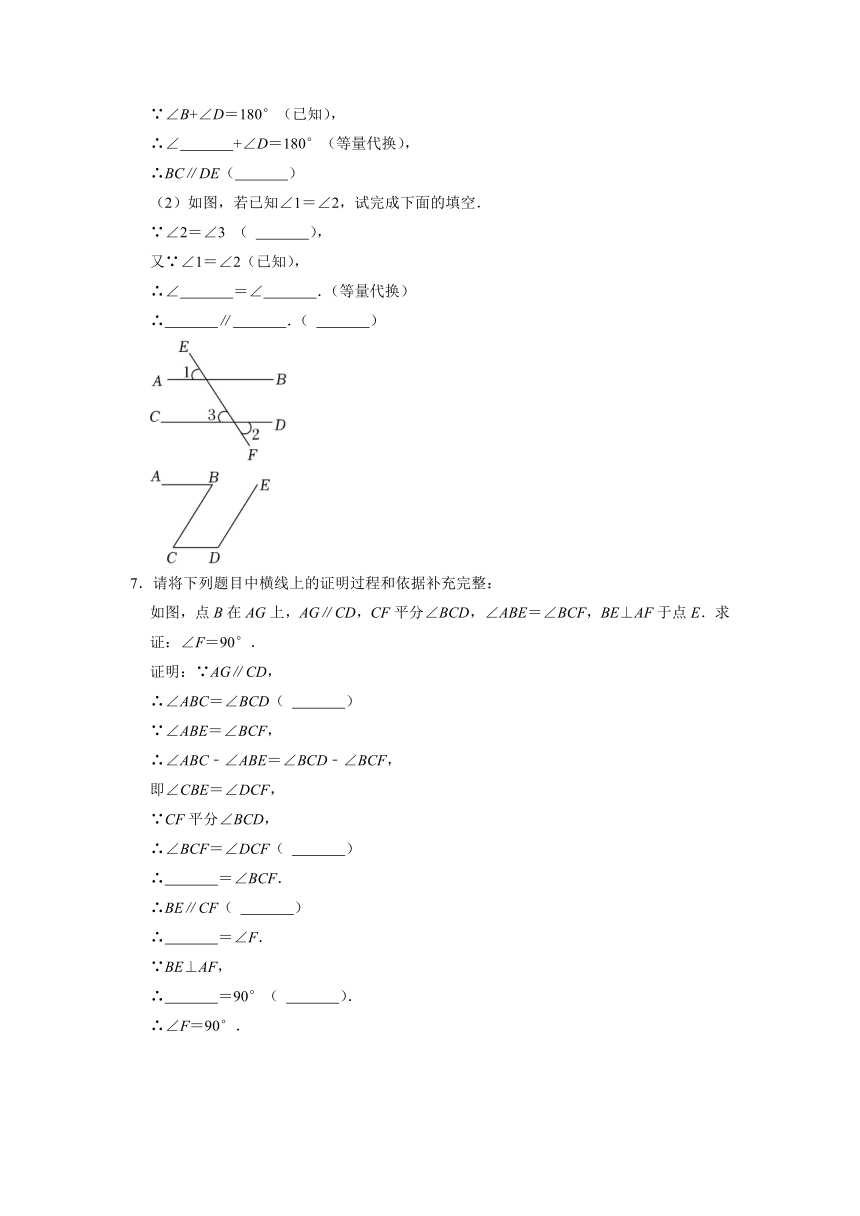
(2)如图,若已知∠1=∠2,试完成下面的填空.
∵∠2=∠3 ( ),
又∵∠1=∠2(已知),
∴∠ =∠ .(等量代换)
∴ ∥ .( )
7.请将下列题目中横线上的证明过程和依据补充完整:
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠BCF,BE⊥AF于点E.求证:∠F=90°.
证明:∵AG∥CD,
∴∠ABC=∠BCD( )
∵∠ABE=∠BCF,
∴∠ABC﹣∠ABE=∠BCD﹣∠BCF,
即∠CBE=∠DCF,
∵CF平分∠BCD,
∴∠BCF=∠DCF( )
∴ =∠BCF.
∴BE∥CF( )
∴ =∠F.
∵BE⊥AF,
∴ =90°( ).
∴∠F=90°.
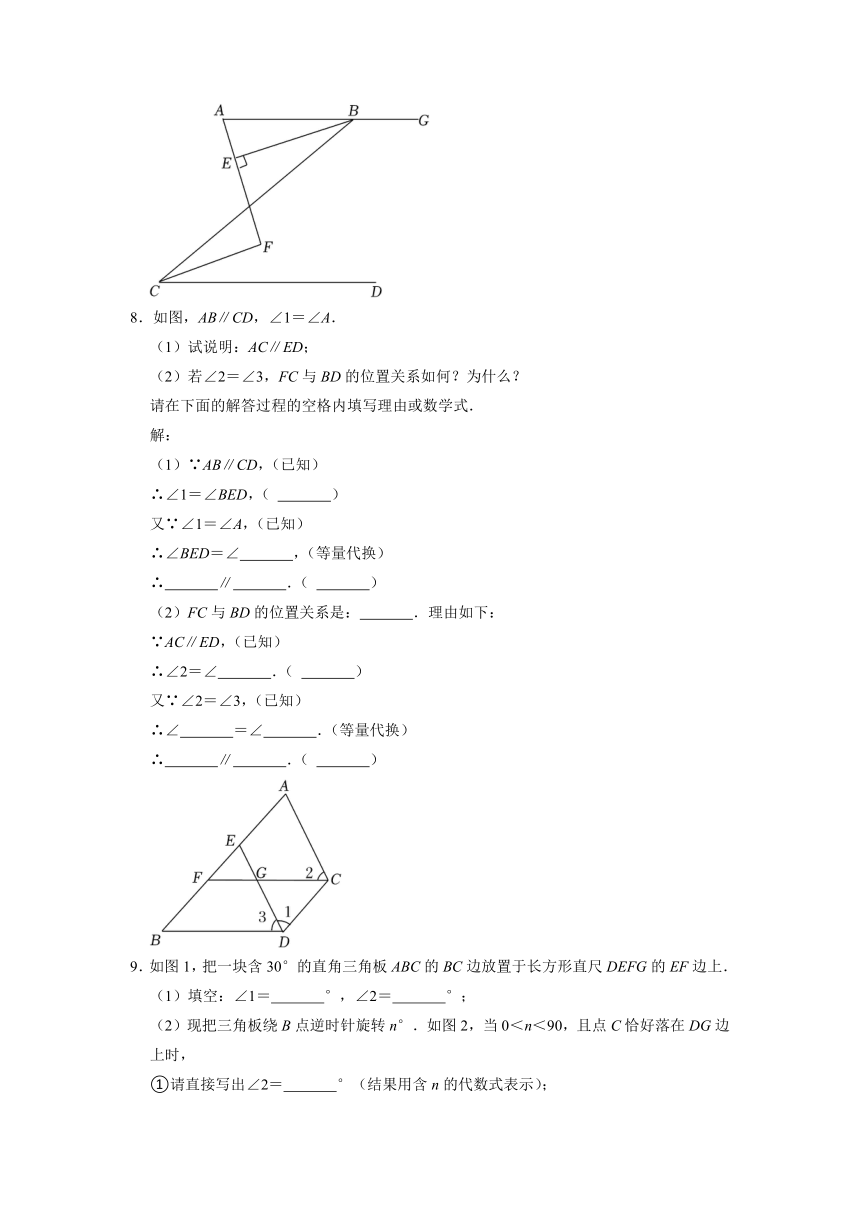
8.如图,AB∥CD,∠1=∠A.
(1)试说明:AC∥ED;
(2)若∠2=∠3,FC与BD的位置关系如何?为什么?
请在下面的解答过程的空格内填写理由或数学式.
解:
(1)∵AB∥CD,(已知)
∴∠1=∠BED,( )
又∵∠1=∠A,(已知)
∴∠BED=∠ ,(等量代换)
∴ ∥ .( )
(2)FC与BD的位置关系是: .理由如下:
∵AC∥ED,(已知)
∴∠2=∠ .( )
又∵∠2=∠3,(已知)
∴∠ =∠ .(等量代换)
∴ ∥ .( )
9.如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:∠1= °,∠2= °;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出∠2= °(结果用含n的代数式表示);
②若∠1与∠2恰好有一个角是另一个角的倍,求n的值.
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
10.在学行线的有关知识后,小明对下面的问题进行了研究.
问题:如图1,AB∥CD,点E在直线AB与CD之间,连结AE,CE,
试说明∠BAE+∠DCE=∠AEC.
(1)下面是小明的解题过程,请你填空.
解:过点E作EF∥AB,
∴∠BAE=∠1( ).
∵CD∥AB(已知),
∴EF∥CD( ).
∴∠DCE=∠2(两直线平行,内错角相等).
∴∠BAE+∠DCE=∠1+∠2(等式的性质).
∴∠BAE+∠DCE=∠AEC(等量代换).
(2)如图2,AD∥BC,点E在线段AB上运动(点E不与点A,B重合),连结CE,DE,若∠ADE=α,∠BCE=β.试说明∠CED,α,β之间的数量关系(写出过程,不需要注明依据).
(3)如图3,AD∥BC,点E在直线AB上运动(点E不与点A,B,O重合),连结CE,DE,若∠ADE=α,∠BCE=β,则∠CED,α,β之间的数量关系是 .
11.阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FG∥CD,∠1=∠3.
求证:∠B+∠BDE=180°.
证明:因为FG∥CD(已知),
所以∠1= .
又因为∠1=∠3(已知),
所以∠2= (等量代换).
所以BC∥ ( ),
所以∠B+∠BDE=180°( ).
12.按要求完成下列证明:
如图:AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.求证:AE∥DF.
证明:∵AB∥CD(已知),
∴∠BAC=∠DCE( ).
∵∠BAC+∠CDF=180°( ),
∴ +∠CDF=180°( ),
∴AE∥DF( ).
13.请完成下面的推理过程:
如图,已知∠D=108°,∠BAD=72°,AC⊥BC于C,EF⊥BC于F.
求证:∠1=∠2.
证明:∵∠D=108°,∠BAD=72°(已知)
∴∠D+∠BAD=180°
∴AB∥CD( )
∴∠1= ( )
又∵AC⊥BC于C,EF⊥BC于F(已知)
∴EF∥ ( )
∴∠2= ( )
∴∠1=∠2( )
14.阅读下列推理过程,在括号中填写理由.
如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( )
∴EF∥AD ( )
∴ +∠2=180° ( )
又∵∠2+∠3=180°(已知)
∴∠1= ( )
∴ ∥ ( )
∴∠GDC=∠B ( )
15.如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G,求证:AB∥CD.
证明:∵AF⊥CE(已知),
∴∠CGF=90°(垂直的定义),
∵∠1=∠D(已知),
∴AF∥ ( ),
∴∠4= =90°( ),
又∵∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵∠2与∠C互余(已知),
∴∠2+∠C=90°,
∴∠C= ,
∴AB∥ .( )
16.如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.
(1)∵∠1=∠2(已知)
∴ ∥CD( )
∴∠ABD+∠CDB= ( )
(2)∵∠BAC=65°,∠ACD=115°,(已知)
∴∠BAC+∠ACD=180°(等式性质)
∴AB∥CD( )
(3)∵CD⊥EF于D,EF⊥AB于F,∠BAC=55°,(已知)
∴∠ABD=∠CDF=90°(垂直的定义)
∴ ∥ (同位角相等,两直线平行)
又∵∠BAC=55°,(已知)
∴∠ACD= .( )
17.在下面解答中填空.
如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
解:∵AB⊥BF,CD⊥BF(已知),
∴∠ABF=∠ =90°(垂直的定义).
∴AB∥CD( ).
∵∠1=∠2(已知),
∴AB∥EF( ).
∴CD∥EF(平行于同一条直线的两条直线互相平行).
∴∠3=∠E( ).
18.填写下面证明过程中的推理依据:
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
(1)∠1=∠2吗?请说明理由
(2)BE与CF的位置关系如何?为什么?
(本题第(1)小题在下面的解答过程的空格内填写理由或数学式;第(2)小题要写出解题过程)
解:(1)∠1=∠2,理由如下:
∵AB∥CD( ),
∴∠ABC=∠BCD( ).
∵BE平分∠ABC,CF平分∠BCD(已知),
∴∠1=∠ (角平分线的定义),
∠2=∠ (角平分线的定义).
∴∠1=∠2( ).
(2)
19.如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
(1)试说明:∠BAG=∠BGA;
(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.
(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.
20.(1)【问题】
如图1,若AB∥CD,∠BEP=25°,∠PFC=150°.求∠EPF的度数;
(2)【问题迁移】
如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)【联想拓展】
如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
参考答案
1.解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴∠B=∠DEC(两直线平行,同位角相等).
又∵∠B=∠D(已知),
∴∠D=∠DEC(等量代换),
∴AD∥BC(内错角相等,两直线平行)、
故答案为:∠B,两直线平行,同位角相等,∠DEC,内错角相等,两直线平行.
2.证明:∵BD平分∠ABC,EF平分∠AED,
∴∠1=∠AED,∠2=∠ABC(角平分线的定义),
∵BC∥ED,
∴∠AED=∠ABC(两直线平行,同位角相等),
∴∠AED=∠ABC,
∴∠1=∠2(等量代换),
∴BD∥EF(同位角相等,两直线平行),
故答案为:角平分线的定义,∠ABC,两直线平行,同位角相等,等量代换,同位角相等,两直线平行.
3.解:(1)作EH∥AB,如图,
∵AB∥CD,
∴EH∥CD,
∴∠1=∠AME,∠2=∠CNE,
∴∠MEN=∠AME+∠CNE,
∵EM是∠AMF的平分线,
∴∠AME=∠AMF,
∴∠MEN=∠AMF+∠CNE=×52°+38°=64°;
同理可得∠MFN=∠AMF+∠CNE=52°+×38°=71°;
(2)∵∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MFN=2∠AMF+∠CNE,
∴2∠MFN﹣∠MEN=∠AMF,
∵2∠MFN﹣∠MEN=45°,
∴∠AMF=45°,
∴∠AMF=30°;
(3)与(1)的证明方法一样可得∠MON=∠AMF+∠CNE,
而∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MEN=∠AMF+2∠CNE,2∠MFN=2∠AMF+∠CNE,
∴2∠MEN+2∠MFN=3(∠AMF+∠CNE),
∴∠AMF+∠CNE=(∠MEN+∠MFN),
∴∠MON=(∠MEN+∠MFN).
4.解:(1)过点P作PR∥AB,
∵AB∥CD,
∴AB∥CD∥PR,
∴∠MPR=∠PMA=α,∠RPQ=∠PQC=β,
∴∠MPQ=∠MPR+∠RPQ=α+β,
∵PQ平分∠MPN,
∴∠NPQ=∠MPQ=α+β;
(2)如图②,EF⊥PQ,理由如下:
∵PQ平分∠MPN.
∴∠MPQ=∠NPQ=α+β,
∵QE∥PN,
∴∠EQP=∠NPQ=α+β,
∴∠EPQ=∠EQP=α+β,
∵EF平分∠PEQ,
∴∠PEQ=2∠PEF=2∠QEF,
∵∠EPQ+∠EQP+∠PEQ=180°,
∴2∠EPQ+2∠PEF=180°,
∴∠EPQ+∠PEF=90°,
∴∠PFE=180°﹣90°=90°,
∴EF⊥PQ;
(3)由(2)可知:∠EQP=∠AMP+∠PQC,∠EFQ=90°,
∴∠QEF=90°﹣(∠AMP+∠PQC),
∴∠NQE=∠PQC+∠EQP=∠AMP+2∠PQC,
∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE
=180°﹣[90°﹣(∠AMP+∠PQC)]﹣(∠AMP+2∠PQC)﹣∠QNE
=180°﹣90°+∠AMP+∠PQC﹣∠AMP﹣2∠PQC﹣∠QNE
=90°﹣∠PQC﹣∠QNE,
∵∠NEF=∠AMP,
∴90°﹣∠PQC﹣∠QNE=∠AMP,
即∠APM+2∠PQC+2∠QNE=180°,
∴∠NQE+2∠QNE=180°,
∵∠NQE+∠QNE+∠NEQ=180°,
∴∠QNE=∠NEQ,
∵QE∥PN,
∴∠PNE=∠QEN,
∴∠PNE=∠QNE,
∴NE平分∠PNQ.
5.解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( 同位角相等,两直线平行),
∴∠3+∠ACB=180°,( 两直线平行,同旁内角互补),
∴∠ACB=50°,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( 同旁内角互补,两直线平行).
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;50;同旁内角互补,两直线平行.
6.(1)证明:∵AB∥CD(已知),
∴∠B=∠C( 两直线平行,内错角相等).
∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换),
∴BC∥DE( 同旁内角互补,两直线平行);
故答案为:B;C;两直线平行,内错角相等;C;同旁内角互补,两直线平行;
(2)证明:∵∠2=∠3 ( 对顶角相等),
又∵∠1=∠2(已知),
∴∠1=∠3.(等量代换)
∴AB∥CD.( 同位角相等,两直线平行);
故答案为:对顶角相等;1;3;AB;CD;同位角相等,两直线平行.
7.证明:∵AG∥CD,
∴∠ABC=∠BCD( 两直线平行,内错角相等),
∵∠ABE=∠BCF,
∴∠ABC﹣∠ABE=∠BCD﹣∠BCF,
即∠CBE=∠DCF,
∵CF平分∠BCD,
∴∠BCF=∠DCF( 角平分线的定义),
∴∠CBE=∠BCF.
∴BE∥CF( 内错角相等,两直线平行),
∴∠BEF=∠F.
∵BE⊥AF,
∴∠BEF=90°( 垂直的定义).
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠CBE;内错角相等,两直线平行;∠BEF;∠BEF;垂直的定义.
8.解:(1)∵AB∥CD(已知),
∴∠1=∠BED( 两直线平行,内错角相等),
又∵∠1=∠A(已知),
∴∠BED=∠A(等量代换),
∴AC∥DE( 同位角相等,两直线平行).
故答案为:两直线平行,内错角相等;A;AC;DE;同位角相等,两直线平行;
(2)FC与BD的位置关系是:FC∥BD.理由如下:
∵AC∥ED(已知),
∴∠2=∠CGD( 两直线平行,内错角相等),
又∵∠2=∠3(已知),
∴∠CGD=∠3(等量代换),
∴FC∥BD( 内错角相等,两直线平行).
故答案为:FC∥BD;CGD;两直线平行,内错角相等;CGD;3;FC;BD;内错角相等,两直线平行.
9.解:(1)∠1=180°﹣60°=120°,
∠2=90°;
故答案为:120,90;
(2)①如图2,∵DG∥EF,
∴∠BCG=180°﹣∠CBF=180°﹣n°,
∵∠ACB+∠BCG+∠2=360°,
∴∠2=360°﹣∠ACB﹣∠BCG
=360°﹣90°﹣(180°﹣n°)
=(90+n)°;
故答案为:(90+n);
②∵∠ABC=60°,
∴∠ABE=180°﹣60°﹣n°=120°﹣n°,
∵DG∥EF
∴∠1=∠ABE=120°﹣n°,
当∠1=∠2时,120﹣n=(90+n),
解得n=;
当∠1=∠2时,(120﹣n)=90+n,
解得n=;
综上所述,n值为或;
(3)当n=60°时,AB⊥DE (GF);
当n=90°时,BC⊥DG (EF),AC⊥DE(GF);
当n=150°时,AB⊥DG (EF);
当n=180°时,AC⊥DG (EF),BC⊥DE(GF);
当n=240°时,AB⊥DE(GF);
当n=270°时,BC⊥DG(EF),AC⊥DE(GF);
当n=330°时,AB⊥DG(EF).
10.解:(1)过点E作EF∥AB,
∴∠BAE=∠1( 两直线平行,内错角相等).
∵CD∥AB(已知),
∴EF∥CD( 平行于同一条直线的两条直线平行).
∴∠DCE=∠2(两直线平行,内错角相等).
∴∠BAE+∠DCE=∠1+∠2(等式的性质).
∴∠BAE+∠DCE=∠AEC(等量代换).
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;
(2)∠CED=α+β,证明如下:
过点E作EF∥AD交CD于点F,如图:
∵EF∥AD,
∴∠DEF=∠ADE=α,
∵BC∥AD,
∴EF∥BC,
∴∠CEF=∠BCE=β,
∴∠CED=∠DEF+∠CEF=α+β;
(3)分三种情况:
(Ⅰ)E在线段BA延长线上,过E作EG∥AD交直线CD于G,如图:
同(2)可证∠BCE=∠CEG=β,∠ADE=∠DEG=α,
∴∠CED=∠CEG﹣∠DEG=β﹣α;
(Ⅱ)E在线段AB上,由(2)知∠CED=α+β;
(Ⅲ)E在线段AB延长线上,过E作EH∥AD交直线CD于H,如图:
同理可证∠BCE=∠CEH=β,∠ADE=∠DEH=α,
∴∠CED=∠DEH﹣∠CEH=α﹣β;
故答案为:∠CED=α+β或∠CED=α﹣β或∠CED=β﹣α.
11.证明:因为FG∥CD(已知),
所以∠1=∠2.
又因为∠1=∠3(已知),
所以∠2=∠3(等量代换).
所以BC∥DE( 内错角相等,两直线平行),
所以∠B+∠BDE=180°( 两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
12.证明:∵AB∥CD(已知),
∴∠BAC=∠DCE( 两直线平行,同位角相等).
∵∠BAC+∠CDF=180°( 已知),
∴∠DCE+∠CDF=180°( 等量代换),
∴AE∥DF( 同旁内角互补,两直线平行).
13.证明:∵∠D=108°,∠BAD=72°(已知),
∴∠D+∠BAD=180°,
∴AB∥CD( 同旁内角互补,两直线平行),
∴∠1=∠3( 两直线平行,内错角相等),
又∵AC⊥BC于C,EF⊥BC于F(已知),
∴EF∥AC( 同位角相等,两直线平行),
∴∠2=∠3( 两直线平行,同位角相等),
∴∠1=∠2( 等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;AC;同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
14.解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90° ( 垂直的定义),
∴EF∥AD ( 同位角相等,两直线平行),
∴∠1+∠2=180° ( 两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3( 同角的补角相等),
∴AB∥DG( 内错角相等,两直线平行),
∴∠GDC=∠B ( 两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;∠3;同角的补角相等;AB;DG;内错角相等,两直线平行;两直线平行,同位角相等.
15.证明:∵AF⊥CE(已知),
∴∠CGF=90°(垂直的定义),
∵∠1=∠D(已知),
∴AF∥DE( 同位角相等,两直线平行),
∴∠4=∠CGF=90°( 两直线平行,同位角相等),
又∵∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵∠2与∠C互余(已知),
∴∠2+∠C=90°,
∴∠C=∠3,
∴AB∥CD( 内错角相等,两直线平行).
故答案为:DE;同位角相等,两直线平行;∠CGF;两直线平行,同位角相等;∠3;CD;内错角相等,两直线平行.
16.解:(1)∵∠1=∠2(已知),
∴AB∥CD( 内错角相等,两直线平行),
∴∠ABD+∠CDB=180°( 两直线平行,同旁内角互补),
故答案为:AB,内错角相等,两直线平行,180°,两直线平行,同旁内角互补;
(2)∵∠BAC=65°,∠ACD=115°,(已知),
∴∠BAC+∠ACD=180°(等式性质),
∴AB∥CD( 同旁内角互补,两直线平行),
故答案为:同旁内角互补,两直线平行;
(3)∵CD⊥EF于D,EF⊥AB于F,∠BAC=55°,(已知),
∴∠ABD=∠CDF=90°(垂直的定义),
∴AB∥CD(同位角相等,两直线平行),
又∵∠BAC=55°,(已知),
∴∠ACD=125°.( 两直线平行,同旁内角互补),
故答案为:AB,CD,125°,两直线平行,同旁内角互补.
17.解:∵AB⊥BF,CD⊥BF(已知),
∴∠ABF=∠CDF=90°(垂直的定义).
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠2(已知),
∴AB∥EF(内错角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线互相平行).
∴∠3=∠E(两直线平行,同位角相等).
故答案为:CDF.
同位角相等,两直线平行.
内错角相等,两直线平行.
两直线平行,同位角相等.
18.解:(1)∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵BE平分∠ABC,CF平分∠BCD(已知),
∴∠1=∠ABC(角平分线的定义),
∠2=∠BCD(角平分线的定义).
∴∠1=∠2(等量代换),
故答案为:已知,两直线平行,内错角相等,ABC,BCD,等量代换;
(2)BE∥CF;
由(1)知∠ABC=∠BCD,∠1=∠2,
∵∠EBC=∠ABC﹣∠1,
∠BCF=∠BCD﹣∠2,
∴∠EBC=∠BCF,
∴BE∥CF.
19.(1)证明:∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD
∴∠BAG=∠BGA;
(2)解:∵∠BGA=∠F+∠BCF,
∴∠BGA﹣∠F=∠BCF,
∵∠BAG=∠BGA,
∴∠∠BAG﹣∠F=∠BCF,
∵∠BAG﹣∠F=45°,
∴∠BCF=45°,
∵∠BCD=90°,
∴CF平分∠BCD;
(3)解:有两种情况:
①当M在BP的下方时,如图5,
设∠ABC=4x,
∵∠ABP=3∠PBG,
∴∠ABP=3x,∠PBG=x,
∵AG∥CH,
∴∠BCH=∠AGB==90°﹣2x,
∵∠BCD=90°,
∴∠DCH=∠PBM=90°﹣(90°﹣2x)=2x,
∴∠ABM=∠ABP+∠PBM=3x+2x=5x,
∠GBM=2x﹣x=x,
∴∠ABM:∠GBM=5x:x=5;
②当M在BP的上方时,如图6,
同理得:∠ABM=∠ABP﹣∠PBM=3x﹣2x=x,
∠GBM=2x+x=3x,
∴∠ABM:∠GBM=x:3x=.
综上,的值是5或.
20.解:(1)如图1,过点P作PQ∥AB,
∵PQ∥AB,AB∥CD,
∴CD∥PQ.
∴∠CFP+∠FPQ=180°
∴∠FPQ=180°﹣150°=30°,
又∵PQ∥AB,
∴∠BEP=∠EPQ=25°,
∴∠EPF=∠EPQ+∠FPQ=25°+30°=55°;
(2)∠PFC=∠PEA+∠P,
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)如图3,过点G作AB的平行线GH.
∵GH∥AB,AB∥CD,
∴GH∥AB∥CD,
∴∠HGE=∠AEG,∠HGF=∠CFG,
又∵∠PEA的平分线和∠PFC的平分线交于点G,
∴∠HGE=∠AEG=∠AEP,∠HGF=∠CFG=∠CFP,
同(1)易得,∠CFP=∠P+∠AEP,
∴∠HGF=(∠P+∠AEP)=(α+∠AEP),
∴∠EGF=∠HGF﹣∠HGE=(α+∠AEP)=α+∠AEP﹣∠HGE=α.
1.如图,已知AB⊥AC,DE⊥AC,∠B=∠D.试说明:AD∥BC.
在下列解答中,填上适当的理由或数学式.
解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴ =∠DEC( ).
又∵∠B=∠D(已知),
∴∠D= (等量代换),
∴AD∥BC( ).
2.请补全证明过程及推理依据.
已知:如图,BC∥ED,BD平分∠ABC,EF平分∠AED.
求证:BD∥EF.
证明:∵BD平分∠ABC,EF平分∠AED,
∴∠1=∠AED,∠2=∠ABC( ).
∵BC∥ED,
∴∠AED= ( )
∴∠AED=∠ABC.
∴∠1=∠2( ).
∴BD∥EF( ).
3.如图,AB∥CD,EM是∠AMF的平分线,NF是∠CNE的平分线,EN、MF交于点O.
(1)若∠AMF=52°,∠CNE=38°,求∠MEN、∠MFN的度数;
(2)若2∠MFN﹣∠MEN=45°,求出∠AMF的度数;
(3)探究∠MEN、∠MFN与∠MON之间存在怎样的数量关系.(直接写出结果)
4.已知AB∥CD,点M在直线AB上,点N、Q在直线CD上,点P在直线AB、CD之间,连接PM、PN、PQ,PQ平分∠MPN,如图①.
(1)若∠PMA=α、∠PQC=β,求∠NPQ的度数(用含α,β的式子表示);
(2)过点Q作QE∥PN交PM的延长线于点E,过E作EF平分∠PEQ交PQ于点F,如图②,请你判断EF与PQ的位置关系,并说明理由;
(3)在(2)的条件下,连接EN,如图③,若∠NEF=∠PMA,求证:NE平分∠PNQ.
5.如图,一个由4条线段构成的“鱼”形图案,其中∠1=50°,∠2=50°,∠3=130°,找出图中的平行线,∠ACB的度数,并说明理由.
解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( ),
∴∠3+∠ACB=180°,( ),
∴∠ACB= °,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( ).
6.完成下列推理过程.
(1)如图,已知AB∥CD,∠B+∠D=180°.
求证:BC∥DE.
证明:∵AB∥CD(已知),
∴∠ =∠ ( ).
∵∠B+∠D=180°(已知),
∴∠ +∠D=180°(等量代换),
∴BC∥DE( )
(2)如图,若已知∠1=∠2,试完成下面的填空.
∵∠2=∠3 ( ),
又∵∠1=∠2(已知),
∴∠ =∠ .(等量代换)
∴ ∥ .( )
7.请将下列题目中横线上的证明过程和依据补充完整:
如图,点B在AG上,AG∥CD,CF平分∠BCD,∠ABE=∠BCF,BE⊥AF于点E.求证:∠F=90°.
证明:∵AG∥CD,
∴∠ABC=∠BCD( )
∵∠ABE=∠BCF,
∴∠ABC﹣∠ABE=∠BCD﹣∠BCF,
即∠CBE=∠DCF,
∵CF平分∠BCD,
∴∠BCF=∠DCF( )
∴ =∠BCF.
∴BE∥CF( )
∴ =∠F.
∵BE⊥AF,
∴ =90°( ).
∴∠F=90°.
8.如图,AB∥CD,∠1=∠A.
(1)试说明:AC∥ED;
(2)若∠2=∠3,FC与BD的位置关系如何?为什么?
请在下面的解答过程的空格内填写理由或数学式.
解:
(1)∵AB∥CD,(已知)
∴∠1=∠BED,( )
又∵∠1=∠A,(已知)
∴∠BED=∠ ,(等量代换)
∴ ∥ .( )
(2)FC与BD的位置关系是: .理由如下:
∵AC∥ED,(已知)
∴∠2=∠ .( )
又∵∠2=∠3,(已知)
∴∠ =∠ .(等量代换)
∴ ∥ .( )
9.如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:∠1= °,∠2= °;
(2)现把三角板绕B点逆时针旋转n°.如图2,当0<n<90,且点C恰好落在DG边上时,
①请直接写出∠2= °(结果用含n的代数式表示);
②若∠1与∠2恰好有一个角是另一个角的倍,求n的值.
(3)若把三角板绕B点顺时针旋转n°.当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有n的值和对应的那两条垂线;如果不存在,请说明理由.
10.在学行线的有关知识后,小明对下面的问题进行了研究.
问题:如图1,AB∥CD,点E在直线AB与CD之间,连结AE,CE,
试说明∠BAE+∠DCE=∠AEC.
(1)下面是小明的解题过程,请你填空.
解:过点E作EF∥AB,
∴∠BAE=∠1( ).
∵CD∥AB(已知),
∴EF∥CD( ).
∴∠DCE=∠2(两直线平行,内错角相等).
∴∠BAE+∠DCE=∠1+∠2(等式的性质).
∴∠BAE+∠DCE=∠AEC(等量代换).
(2)如图2,AD∥BC,点E在线段AB上运动(点E不与点A,B重合),连结CE,DE,若∠ADE=α,∠BCE=β.试说明∠CED,α,β之间的数量关系(写出过程,不需要注明依据).
(3)如图3,AD∥BC,点E在直线AB上运动(点E不与点A,B,O重合),连结CE,DE,若∠ADE=α,∠BCE=β,则∠CED,α,β之间的数量关系是 .
11.阅读下面的推理过程,将空白部分补充完整.
已知:如图,在△ABC中,FG∥CD,∠1=∠3.
求证:∠B+∠BDE=180°.
证明:因为FG∥CD(已知),
所以∠1= .
又因为∠1=∠3(已知),
所以∠2= (等量代换).
所以BC∥ ( ),
所以∠B+∠BDE=180°( ).
12.按要求完成下列证明:
如图:AB∥CD,直线AE交CD于点C,∠BAC+∠CDF=180°.求证:AE∥DF.
证明:∵AB∥CD(已知),
∴∠BAC=∠DCE( ).
∵∠BAC+∠CDF=180°( ),
∴ +∠CDF=180°( ),
∴AE∥DF( ).
13.请完成下面的推理过程:
如图,已知∠D=108°,∠BAD=72°,AC⊥BC于C,EF⊥BC于F.
求证:∠1=∠2.
证明:∵∠D=108°,∠BAD=72°(已知)
∴∠D+∠BAD=180°
∴AB∥CD( )
∴∠1= ( )
又∵AC⊥BC于C,EF⊥BC于F(已知)
∴EF∥ ( )
∴∠2= ( )
∴∠1=∠2( )
14.阅读下列推理过程,在括号中填写理由.
如图,已知AD⊥BC,EF⊥BC,垂足分别为D、F,∠2+∠3=180°.
试说明:∠GDC=∠B.
解:∵AD⊥BC,EF⊥BC(已知)
∴∠ADB=∠EFB=90° ( )
∴EF∥AD ( )
∴ +∠2=180° ( )
又∵∠2+∠3=180°(已知)
∴∠1= ( )
∴ ∥ ( )
∴∠GDC=∠B ( )
15.如图,E、F分别在AB和CD上,∠1=∠D,∠2与∠C互余,AF⊥CE于G,求证:AB∥CD.
证明:∵AF⊥CE(已知),
∴∠CGF=90°(垂直的定义),
∵∠1=∠D(已知),
∴AF∥ ( ),
∴∠4= =90°( ),
又∵∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵∠2与∠C互余(已知),
∴∠2+∠C=90°,
∴∠C= ,
∴AB∥ .( )
16.如图,AB与EF交于点B,CD与EF交于点D,根据图形,请补全下面这道题的解答过程.
(1)∵∠1=∠2(已知)
∴ ∥CD( )
∴∠ABD+∠CDB= ( )
(2)∵∠BAC=65°,∠ACD=115°,(已知)
∴∠BAC+∠ACD=180°(等式性质)
∴AB∥CD( )
(3)∵CD⊥EF于D,EF⊥AB于F,∠BAC=55°,(已知)
∴∠ABD=∠CDF=90°(垂直的定义)
∴ ∥ (同位角相等,两直线平行)
又∵∠BAC=55°,(已知)
∴∠ACD= .( )
17.在下面解答中填空.
如图,AB⊥BF,CD⊥BF,∠1=∠2,试说明∠3=∠E.
解:∵AB⊥BF,CD⊥BF(已知),
∴∠ABF=∠ =90°(垂直的定义).
∴AB∥CD( ).
∵∠1=∠2(已知),
∴AB∥EF( ).
∴CD∥EF(平行于同一条直线的两条直线互相平行).
∴∠3=∠E( ).
18.填写下面证明过程中的推理依据:
已知:如图,AB∥CD,BE平分∠ABC,CF平分∠BCD.
(1)∠1=∠2吗?请说明理由
(2)BE与CF的位置关系如何?为什么?
(本题第(1)小题在下面的解答过程的空格内填写理由或数学式;第(2)小题要写出解题过程)
解:(1)∠1=∠2,理由如下:
∵AB∥CD( ),
∴∠ABC=∠BCD( ).
∵BE平分∠ABC,CF平分∠BCD(已知),
∴∠1=∠ (角平分线的定义),
∠2=∠ (角平分线的定义).
∴∠1=∠2( ).
(2)
19.如图,AD∥BC,∠BAD的平分线交BC于点G,∠BCD=90°.
(1)试说明:∠BAG=∠BGA;
(2)如图1,点F在AG的反向延长线上,连接CF交AD于点E,若∠BAG﹣∠F=45°,求证:CF平分∠BCD.
(3)如图2,线段AG上有点P,满足∠ABP=3∠PBG,过点C作CH∥AG.若在直线AG上取一点M,使∠PBM=∠DCH,求的值.
20.(1)【问题】
如图1,若AB∥CD,∠BEP=25°,∠PFC=150°.求∠EPF的度数;
(2)【问题迁移】
如图2,AB∥CD,点P在AB的上方,问∠PEA,∠PFC,∠EPF之间有何数量关系?请说明理由;
(3)【联想拓展】
如图3所示,在(2)的条件下,已知∠EPF=α,∠PEA的平分线和∠PFC的平分线交于点G,用含有α的式子表示∠G的度数.
参考答案
1.解:∵AB⊥AC,DE⊥AC(已知),
∴AB∥DE(在同一平面内,垂直于同一条直线的两条直线平行).
∴∠B=∠DEC(两直线平行,同位角相等).
又∵∠B=∠D(已知),
∴∠D=∠DEC(等量代换),
∴AD∥BC(内错角相等,两直线平行)、
故答案为:∠B,两直线平行,同位角相等,∠DEC,内错角相等,两直线平行.
2.证明:∵BD平分∠ABC,EF平分∠AED,
∴∠1=∠AED,∠2=∠ABC(角平分线的定义),
∵BC∥ED,
∴∠AED=∠ABC(两直线平行,同位角相等),
∴∠AED=∠ABC,
∴∠1=∠2(等量代换),
∴BD∥EF(同位角相等,两直线平行),
故答案为:角平分线的定义,∠ABC,两直线平行,同位角相等,等量代换,同位角相等,两直线平行.
3.解:(1)作EH∥AB,如图,
∵AB∥CD,
∴EH∥CD,
∴∠1=∠AME,∠2=∠CNE,
∴∠MEN=∠AME+∠CNE,
∵EM是∠AMF的平分线,
∴∠AME=∠AMF,
∴∠MEN=∠AMF+∠CNE=×52°+38°=64°;
同理可得∠MFN=∠AMF+∠CNE=52°+×38°=71°;
(2)∵∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MFN=2∠AMF+∠CNE,
∴2∠MFN﹣∠MEN=∠AMF,
∵2∠MFN﹣∠MEN=45°,
∴∠AMF=45°,
∴∠AMF=30°;
(3)与(1)的证明方法一样可得∠MON=∠AMF+∠CNE,
而∠MEN=∠AMF+∠CNE,∠MFN=∠AMF+∠CNE,
∴2∠MEN=∠AMF+2∠CNE,2∠MFN=2∠AMF+∠CNE,
∴2∠MEN+2∠MFN=3(∠AMF+∠CNE),
∴∠AMF+∠CNE=(∠MEN+∠MFN),
∴∠MON=(∠MEN+∠MFN).
4.解:(1)过点P作PR∥AB,
∵AB∥CD,
∴AB∥CD∥PR,
∴∠MPR=∠PMA=α,∠RPQ=∠PQC=β,
∴∠MPQ=∠MPR+∠RPQ=α+β,
∵PQ平分∠MPN,
∴∠NPQ=∠MPQ=α+β;
(2)如图②,EF⊥PQ,理由如下:
∵PQ平分∠MPN.
∴∠MPQ=∠NPQ=α+β,
∵QE∥PN,
∴∠EQP=∠NPQ=α+β,
∴∠EPQ=∠EQP=α+β,
∵EF平分∠PEQ,
∴∠PEQ=2∠PEF=2∠QEF,
∵∠EPQ+∠EQP+∠PEQ=180°,
∴2∠EPQ+2∠PEF=180°,
∴∠EPQ+∠PEF=90°,
∴∠PFE=180°﹣90°=90°,
∴EF⊥PQ;
(3)由(2)可知:∠EQP=∠AMP+∠PQC,∠EFQ=90°,
∴∠QEF=90°﹣(∠AMP+∠PQC),
∴∠NQE=∠PQC+∠EQP=∠AMP+2∠PQC,
∴∠NEF=180°﹣∠QEF﹣∠NQE﹣∠QNE
=180°﹣[90°﹣(∠AMP+∠PQC)]﹣(∠AMP+2∠PQC)﹣∠QNE
=180°﹣90°+∠AMP+∠PQC﹣∠AMP﹣2∠PQC﹣∠QNE
=90°﹣∠PQC﹣∠QNE,
∵∠NEF=∠AMP,
∴90°﹣∠PQC﹣∠QNE=∠AMP,
即∠APM+2∠PQC+2∠QNE=180°,
∴∠NQE+2∠QNE=180°,
∵∠NQE+∠QNE+∠NEQ=180°,
∴∠QNE=∠NEQ,
∵QE∥PN,
∴∠PNE=∠QEN,
∴∠PNE=∠QNE,
∴NE平分∠PNQ.
5.解:OA∥BC,OB∥AC.
理由:∵∠1=50°,∠2=50°,
∴∠1=∠2(等量代换)
∴OB∥AC. ( 同位角相等,两直线平行),
∴∠3+∠ACB=180°,( 两直线平行,同旁内角互补),
∴∠ACB=50°,
∵∠2=50°,∠3=130°,
∴∠2+∠3=180°,
∴OA∥BC.( 同旁内角互补,两直线平行).
故答案为:同位角相等,两直线平行;两直线平行,同旁内角互补;50;同旁内角互补,两直线平行.
6.(1)证明:∵AB∥CD(已知),
∴∠B=∠C( 两直线平行,内错角相等).
∵∠B+∠D=180°(已知),
∴∠C+∠D=180°(等量代换),
∴BC∥DE( 同旁内角互补,两直线平行);
故答案为:B;C;两直线平行,内错角相等;C;同旁内角互补,两直线平行;
(2)证明:∵∠2=∠3 ( 对顶角相等),
又∵∠1=∠2(已知),
∴∠1=∠3.(等量代换)
∴AB∥CD.( 同位角相等,两直线平行);
故答案为:对顶角相等;1;3;AB;CD;同位角相等,两直线平行.
7.证明:∵AG∥CD,
∴∠ABC=∠BCD( 两直线平行,内错角相等),
∵∠ABE=∠BCF,
∴∠ABC﹣∠ABE=∠BCD﹣∠BCF,
即∠CBE=∠DCF,
∵CF平分∠BCD,
∴∠BCF=∠DCF( 角平分线的定义),
∴∠CBE=∠BCF.
∴BE∥CF( 内错角相等,两直线平行),
∴∠BEF=∠F.
∵BE⊥AF,
∴∠BEF=90°( 垂直的定义).
∴∠F=90°.
故答案为:两直线平行,内错角相等;角平分线的定义;∠CBE;内错角相等,两直线平行;∠BEF;∠BEF;垂直的定义.
8.解:(1)∵AB∥CD(已知),
∴∠1=∠BED( 两直线平行,内错角相等),
又∵∠1=∠A(已知),
∴∠BED=∠A(等量代换),
∴AC∥DE( 同位角相等,两直线平行).
故答案为:两直线平行,内错角相等;A;AC;DE;同位角相等,两直线平行;
(2)FC与BD的位置关系是:FC∥BD.理由如下:
∵AC∥ED(已知),
∴∠2=∠CGD( 两直线平行,内错角相等),
又∵∠2=∠3(已知),
∴∠CGD=∠3(等量代换),
∴FC∥BD( 内错角相等,两直线平行).
故答案为:FC∥BD;CGD;两直线平行,内错角相等;CGD;3;FC;BD;内错角相等,两直线平行.
9.解:(1)∠1=180°﹣60°=120°,
∠2=90°;
故答案为:120,90;
(2)①如图2,∵DG∥EF,
∴∠BCG=180°﹣∠CBF=180°﹣n°,
∵∠ACB+∠BCG+∠2=360°,
∴∠2=360°﹣∠ACB﹣∠BCG
=360°﹣90°﹣(180°﹣n°)
=(90+n)°;
故答案为:(90+n);
②∵∠ABC=60°,
∴∠ABE=180°﹣60°﹣n°=120°﹣n°,
∵DG∥EF
∴∠1=∠ABE=120°﹣n°,
当∠1=∠2时,120﹣n=(90+n),
解得n=;
当∠1=∠2时,(120﹣n)=90+n,
解得n=;
综上所述,n值为或;
(3)当n=60°时,AB⊥DE (GF);
当n=90°时,BC⊥DG (EF),AC⊥DE(GF);
当n=150°时,AB⊥DG (EF);
当n=180°时,AC⊥DG (EF),BC⊥DE(GF);
当n=240°时,AB⊥DE(GF);
当n=270°时,BC⊥DG(EF),AC⊥DE(GF);
当n=330°时,AB⊥DG(EF).
10.解:(1)过点E作EF∥AB,
∴∠BAE=∠1( 两直线平行,内错角相等).
∵CD∥AB(已知),
∴EF∥CD( 平行于同一条直线的两条直线平行).
∴∠DCE=∠2(两直线平行,内错角相等).
∴∠BAE+∠DCE=∠1+∠2(等式的性质).
∴∠BAE+∠DCE=∠AEC(等量代换).
故答案为:两直线平行,内错角相等;平行于同一条直线的两条直线互相平行;
(2)∠CED=α+β,证明如下:
过点E作EF∥AD交CD于点F,如图:
∵EF∥AD,
∴∠DEF=∠ADE=α,
∵BC∥AD,
∴EF∥BC,
∴∠CEF=∠BCE=β,
∴∠CED=∠DEF+∠CEF=α+β;
(3)分三种情况:
(Ⅰ)E在线段BA延长线上,过E作EG∥AD交直线CD于G,如图:
同(2)可证∠BCE=∠CEG=β,∠ADE=∠DEG=α,
∴∠CED=∠CEG﹣∠DEG=β﹣α;
(Ⅱ)E在线段AB上,由(2)知∠CED=α+β;
(Ⅲ)E在线段AB延长线上,过E作EH∥AD交直线CD于H,如图:
同理可证∠BCE=∠CEH=β,∠ADE=∠DEH=α,
∴∠CED=∠DEH﹣∠CEH=α﹣β;
故答案为:∠CED=α+β或∠CED=α﹣β或∠CED=β﹣α.
11.证明:因为FG∥CD(已知),
所以∠1=∠2.
又因为∠1=∠3(已知),
所以∠2=∠3(等量代换).
所以BC∥DE( 内错角相等,两直线平行),
所以∠B+∠BDE=180°( 两直线平行,同旁内角互补).
故答案为:∠2;∠3;DE;内错角相等,两直线平行;两直线平行,同旁内角互补.
12.证明:∵AB∥CD(已知),
∴∠BAC=∠DCE( 两直线平行,同位角相等).
∵∠BAC+∠CDF=180°( 已知),
∴∠DCE+∠CDF=180°( 等量代换),
∴AE∥DF( 同旁内角互补,两直线平行).
13.证明:∵∠D=108°,∠BAD=72°(已知),
∴∠D+∠BAD=180°,
∴AB∥CD( 同旁内角互补,两直线平行),
∴∠1=∠3( 两直线平行,内错角相等),
又∵AC⊥BC于C,EF⊥BC于F(已知),
∴EF∥AC( 同位角相等,两直线平行),
∴∠2=∠3( 两直线平行,同位角相等),
∴∠1=∠2( 等量代换).
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,内错角相等;AC;同位角相等,两直线平行;∠3;两直线平行,同位角相等;等量代换.
14.解:∵AD⊥BC,EF⊥BC(已知),
∴∠ADB=∠EFB=90° ( 垂直的定义),
∴EF∥AD ( 同位角相等,两直线平行),
∴∠1+∠2=180° ( 两直线平行,同旁内角互补),
又∵∠2+∠3=180°(已知),
∴∠1=∠3( 同角的补角相等),
∴AB∥DG( 内错角相等,两直线平行),
∴∠GDC=∠B ( 两直线平行,同位角相等).
故答案为:垂直的定义;同位角相等,两直线平行;∠1;两直线平行,同旁内角互补;∠3;同角的补角相等;AB;DG;内错角相等,两直线平行;两直线平行,同位角相等.
15.证明:∵AF⊥CE(已知),
∴∠CGF=90°(垂直的定义),
∵∠1=∠D(已知),
∴AF∥DE( 同位角相等,两直线平行),
∴∠4=∠CGF=90°( 两直线平行,同位角相等),
又∵∠2+∠3+∠4=180°,
∴∠2+∠3=90°,
∵∠2与∠C互余(已知),
∴∠2+∠C=90°,
∴∠C=∠3,
∴AB∥CD( 内错角相等,两直线平行).
故答案为:DE;同位角相等,两直线平行;∠CGF;两直线平行,同位角相等;∠3;CD;内错角相等,两直线平行.
16.解:(1)∵∠1=∠2(已知),
∴AB∥CD( 内错角相等,两直线平行),
∴∠ABD+∠CDB=180°( 两直线平行,同旁内角互补),
故答案为:AB,内错角相等,两直线平行,180°,两直线平行,同旁内角互补;
(2)∵∠BAC=65°,∠ACD=115°,(已知),
∴∠BAC+∠ACD=180°(等式性质),
∴AB∥CD( 同旁内角互补,两直线平行),
故答案为:同旁内角互补,两直线平行;
(3)∵CD⊥EF于D,EF⊥AB于F,∠BAC=55°,(已知),
∴∠ABD=∠CDF=90°(垂直的定义),
∴AB∥CD(同位角相等,两直线平行),
又∵∠BAC=55°,(已知),
∴∠ACD=125°.( 两直线平行,同旁内角互补),
故答案为:AB,CD,125°,两直线平行,同旁内角互补.
17.解:∵AB⊥BF,CD⊥BF(已知),
∴∠ABF=∠CDF=90°(垂直的定义).
∴AB∥CD(同位角相等,两直线平行).
∵∠1=∠2(已知),
∴AB∥EF(内错角相等,两直线平行).
∴CD∥EF(平行于同一条直线的两条直线互相平行).
∴∠3=∠E(两直线平行,同位角相等).
故答案为:CDF.
同位角相等,两直线平行.
内错角相等,两直线平行.
两直线平行,同位角相等.
18.解:(1)∵AB∥CD(已知),
∴∠ABC=∠BCD(两直线平行,内错角相等).
∵BE平分∠ABC,CF平分∠BCD(已知),
∴∠1=∠ABC(角平分线的定义),
∠2=∠BCD(角平分线的定义).
∴∠1=∠2(等量代换),
故答案为:已知,两直线平行,内错角相等,ABC,BCD,等量代换;
(2)BE∥CF;
由(1)知∠ABC=∠BCD,∠1=∠2,
∵∠EBC=∠ABC﹣∠1,
∠BCF=∠BCD﹣∠2,
∴∠EBC=∠BCF,
∴BE∥CF.
19.(1)证明:∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD
∴∠BAG=∠BGA;
(2)解:∵∠BGA=∠F+∠BCF,
∴∠BGA﹣∠F=∠BCF,
∵∠BAG=∠BGA,
∴∠∠BAG﹣∠F=∠BCF,
∵∠BAG﹣∠F=45°,
∴∠BCF=45°,
∵∠BCD=90°,
∴CF平分∠BCD;
(3)解:有两种情况:
①当M在BP的下方时,如图5,
设∠ABC=4x,
∵∠ABP=3∠PBG,
∴∠ABP=3x,∠PBG=x,
∵AG∥CH,
∴∠BCH=∠AGB==90°﹣2x,
∵∠BCD=90°,
∴∠DCH=∠PBM=90°﹣(90°﹣2x)=2x,
∴∠ABM=∠ABP+∠PBM=3x+2x=5x,
∠GBM=2x﹣x=x,
∴∠ABM:∠GBM=5x:x=5;
②当M在BP的上方时,如图6,
同理得:∠ABM=∠ABP﹣∠PBM=3x﹣2x=x,
∠GBM=2x+x=3x,
∴∠ABM:∠GBM=x:3x=.
综上,的值是5或.
20.解:(1)如图1,过点P作PQ∥AB,
∵PQ∥AB,AB∥CD,
∴CD∥PQ.
∴∠CFP+∠FPQ=180°
∴∠FPQ=180°﹣150°=30°,
又∵PQ∥AB,
∴∠BEP=∠EPQ=25°,
∴∠EPF=∠EPQ+∠FPQ=25°+30°=55°;
(2)∠PFC=∠PEA+∠P,
理由:如图2,过P点作PN∥AB,则PN∥CD,
∴∠PEA=∠NPE,
∵∠FPN=∠NPE+∠FPE,
∴∠FPN=∠PEA+∠FPE,
∵PN∥CD,
∴∠FPN=∠PFC,
∴∠PFC=∠PEA+∠FPE,即∠PFC=∠PEA+∠P;
(3)如图3,过点G作AB的平行线GH.
∵GH∥AB,AB∥CD,
∴GH∥AB∥CD,
∴∠HGE=∠AEG,∠HGF=∠CFG,
又∵∠PEA的平分线和∠PFC的平分线交于点G,
∴∠HGE=∠AEG=∠AEP,∠HGF=∠CFG=∠CFP,
同(1)易得,∠CFP=∠P+∠AEP,
∴∠HGF=(∠P+∠AEP)=(α+∠AEP),
∴∠EGF=∠HGF﹣∠HGE=(α+∠AEP)=α+∠AEP﹣∠HGE=α.
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
