2021-2022学年七年级数学下册 5.1.1相交线 课件(共22张)
文档属性
| 名称 | 2021-2022学年七年级数学下册 5.1.1相交线 课件(共22张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
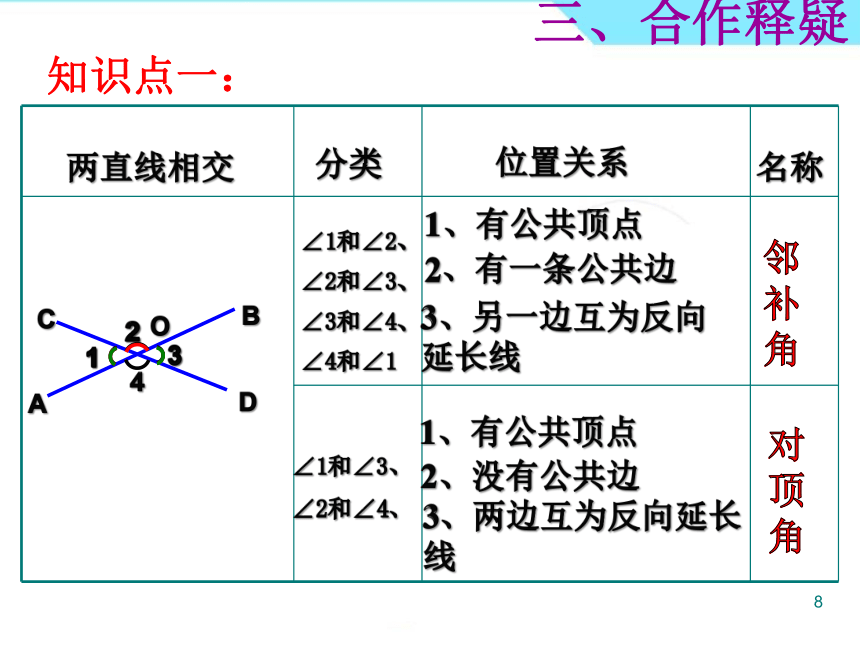
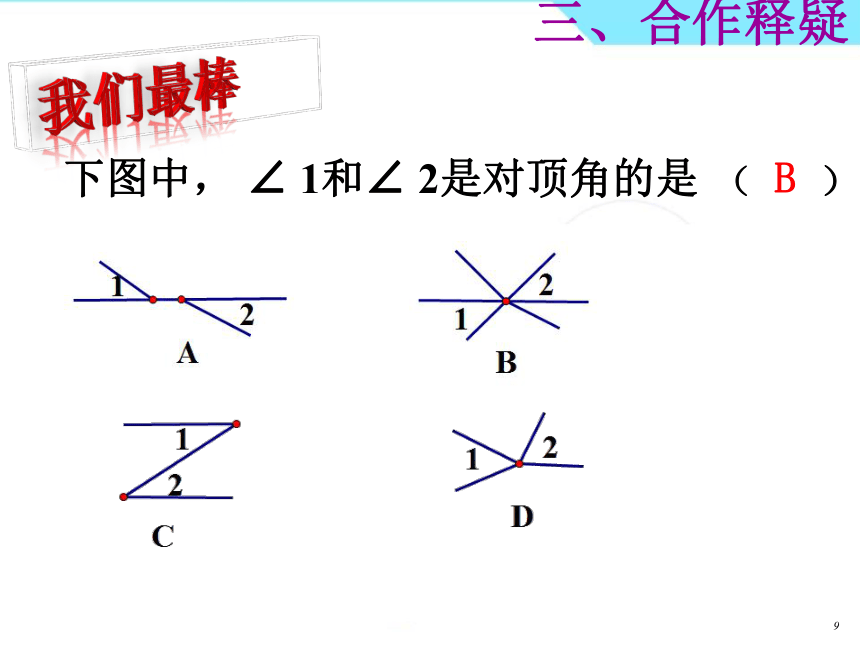
5.1.1相交线义务教育教科书 数学 七年级 下册一、导入展示北京立交桥青马大桥(中国香港)国际象棋中国围棋1、知道对顶角、邻补角的概念.2、理解对顶角和邻补角的性质,会运用它解决相关问题.一、导入展示学习目标请阅读教科书第1~3页并思考:1、两条直线相交,构成的小于平角的角有多少个?这些角两两相配能得到几对角?2、邻补角是怎么定义的?具有什么性质?3、对顶角是怎么定义的?具有什么性质?二、自主学习自学指导8分钟后全班交流展示!知识点一:1、两条直线相交所成的四个角中,有_________,一个角的两边是另一个角的两边的___________,那么这两个角叫做对顶角。2、两条直线相交所成的四个角中,有___________和________,一个角的一边是另一个角的一边的___________.那么这两个角叫作邻补角。三、合作释疑公共顶点反向延长线公共顶点公共边反向延长线BACDO12341、有公共顶点分类∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1∠1和∠3、∠2和∠4、1、有公共顶点位置关系邻补角对顶角2、有一条公共边3、另一边互为反向延长线2、没有公共边两直线相交3、两边互为反向延长线名称1213知识点一:三、合作释疑三、合作释疑我们最棒下图中, ∠1和∠2是对顶角的是( )B如图所示,三条直线AB、CD、EF两两相交,你能说出图中所有的对顶角吗?194BACDEF235678101112如图所示,直线AB、CD、EF相交于一点O,你能说出图中所有对顶角吗?ABCDEFOEABCDOCDFOABEFO三、合作释疑知识点二:性质:1.对顶角_______;2.邻补角之和为_____.相等180°1、有公共顶点分类∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1∠1和∠3、∠2和∠4、1、有公共顶点位置关系邻补角对顶角邻补角互补2、有一条公共边3、另一边互为反向延长线2、没有公共边两直线相交3、两边互为反向延长线名称大小关系对顶角相等BACDO12341312判断:1.互补的角就是邻补角。2.相等的角就是对顶角。3.顶点公共且互补的两个角是邻补角三、合作释疑( )( )( ) 我们最棒三、合作释疑1、若∠1与∠2是对顶角,∠1=16°,则∠2=___°;若∠3与∠4是邻补角,则∠3+∠4=______°2、若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3=°3、图中是对顶角量角器,你能说出用它测量角的原理吗?16180180我们最棒例:如图,直线a、b相交。(1)∠1=400,求∠2,∠3,∠4的度数。(2) ∠1:∠2=2:7 ,求各角的度数。三、合作释疑三、合作释疑直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°。求∠DOE的度数。我们最棒ABCDOE解:∵∠AOC=50°(已知)∴∠AOD=180°—∠AOC=180°—50°=130°(邻补角的定义)∵OE平分∠AOD(已知)∴∠DOE=1/2∠AOD=130°÷2=65°(角平分线的定义)四、总结评价目标再现1、知道对顶角、邻补角的概念.2、理解对顶角和邻补角的性质,会运用它解决相关问题.角的名称邻补角对顶角位置关系2、有一条公共边3、另一边互为反向延长线1、有公共顶点1、有公共顶点2、没有公共边3、两边互为反向延长线性质邻补角互补对顶角相等相同点都有一个公共顶点,它们都是成对出现的不同点对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个四、总结评价1、如图3,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为。2、已知两条直线相交成的四个角,其中一个角是900,其余各角是_____。五、当堂检测必做题图33、如图4,三条直线a,b,c相交于点O,∠1=400,∠2=550,则∠3=_____.选做题五、当堂检测图4两条直线相交于一点,有几对对顶角?三条直线相交于一点,有几对对顶角?四条直线相交于一点,有几对对顶角?n条直线相交于一点,有几对对顶角?五、当堂检测思考题
5.1.1相交线义务教育教科书 数学 七年级 下册一、导入展示北京立交桥青马大桥(中国香港)国际象棋中国围棋1、知道对顶角、邻补角的概念.2、理解对顶角和邻补角的性质,会运用它解决相关问题.一、导入展示学习目标请阅读教科书第1~3页并思考:1、两条直线相交,构成的小于平角的角有多少个?这些角两两相配能得到几对角?2、邻补角是怎么定义的?具有什么性质?3、对顶角是怎么定义的?具有什么性质?二、自主学习自学指导8分钟后全班交流展示!知识点一:1、两条直线相交所成的四个角中,有_________,一个角的两边是另一个角的两边的___________,那么这两个角叫做对顶角。2、两条直线相交所成的四个角中,有___________和________,一个角的一边是另一个角的一边的___________.那么这两个角叫作邻补角。三、合作释疑公共顶点反向延长线公共顶点公共边反向延长线BACDO12341、有公共顶点分类∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1∠1和∠3、∠2和∠4、1、有公共顶点位置关系邻补角对顶角2、有一条公共边3、另一边互为反向延长线2、没有公共边两直线相交3、两边互为反向延长线名称1213知识点一:三、合作释疑三、合作释疑我们最棒下图中, ∠1和∠2是对顶角的是( )B如图所示,三条直线AB、CD、EF两两相交,你能说出图中所有的对顶角吗?194BACDEF235678101112如图所示,直线AB、CD、EF相交于一点O,你能说出图中所有对顶角吗?ABCDEFOEABCDOCDFOABEFO三、合作释疑知识点二:性质:1.对顶角_______;2.邻补角之和为_____.相等180°1、有公共顶点分类∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1∠1和∠3、∠2和∠4、1、有公共顶点位置关系邻补角对顶角邻补角互补2、有一条公共边3、另一边互为反向延长线2、没有公共边两直线相交3、两边互为反向延长线名称大小关系对顶角相等BACDO12341312判断:1.互补的角就是邻补角。2.相等的角就是对顶角。3.顶点公共且互补的两个角是邻补角三、合作释疑( )( )( ) 我们最棒三、合作释疑1、若∠1与∠2是对顶角,∠1=16°,则∠2=___°;若∠3与∠4是邻补角,则∠3+∠4=______°2、若∠1与∠2为对顶角,∠1与∠3互补,则∠2+∠3=°3、图中是对顶角量角器,你能说出用它测量角的原理吗?16180180我们最棒例:如图,直线a、b相交。(1)∠1=400,求∠2,∠3,∠4的度数。(2) ∠1:∠2=2:7 ,求各角的度数。三、合作释疑三、合作释疑直线AB、CD交于点O,OE是∠AOD的平分线,已知∠AOC=50°。求∠DOE的度数。我们最棒ABCDOE解:∵∠AOC=50°(已知)∴∠AOD=180°—∠AOC=180°—50°=130°(邻补角的定义)∵OE平分∠AOD(已知)∴∠DOE=1/2∠AOD=130°÷2=65°(角平分线的定义)四、总结评价目标再现1、知道对顶角、邻补角的概念.2、理解对顶角和邻补角的性质,会运用它解决相关问题.角的名称邻补角对顶角位置关系2、有一条公共边3、另一边互为反向延长线1、有公共顶点1、有公共顶点2、没有公共边3、两边互为反向延长线性质邻补角互补对顶角相等相同点都有一个公共顶点,它们都是成对出现的不同点对顶角没有公共边而邻补角有一条公共边;两条直线相交时,一个角的对顶角只有一个,而一个角的邻补角有两个四、总结评价1、如图3,∠2与∠3为邻补角,∠1=∠2,则∠1与∠3的关系为。2、已知两条直线相交成的四个角,其中一个角是900,其余各角是_____。五、当堂检测必做题图33、如图4,三条直线a,b,c相交于点O,∠1=400,∠2=550,则∠3=_____.选做题五、当堂检测图4两条直线相交于一点,有几对对顶角?三条直线相交于一点,有几对对顶角?四条直线相交于一点,有几对对顶角?n条直线相交于一点,有几对对顶角?五、当堂检测思考题
