2021-2022学年七年级数学下册5.3平行线的判定与性质 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年七年级数学下册5.3平行线的判定与性质 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 12:57:10 | ||
图片预览





文档简介
(共18张PPT)
5.3.4平行线的判定与性质义务教育教科书 数学 七年级 下册一、知识梳理
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
证明直线平行
两直线平行
角相等或互补
证明角相等或互补
学习目标1.巩固平行线的判定与性质;2.灵活运用平行线判定与性质解决问题。3.初步学习证明过程一、知识梳理二、知识运用
A
B
C
D
E
F
1
2
3
填空:
(1)、∵ ∠A=____, (已知)
∴ AC∥ED ,(_____________________ )
2、 ∵AB ∥______, (已知)
∴ ∠2= ∠4,(______________________)
3、 ∵ ___ ∥___, (已知)
∴ ∠B= ∠3. (___________ ___________)
4
5
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
我们最棒
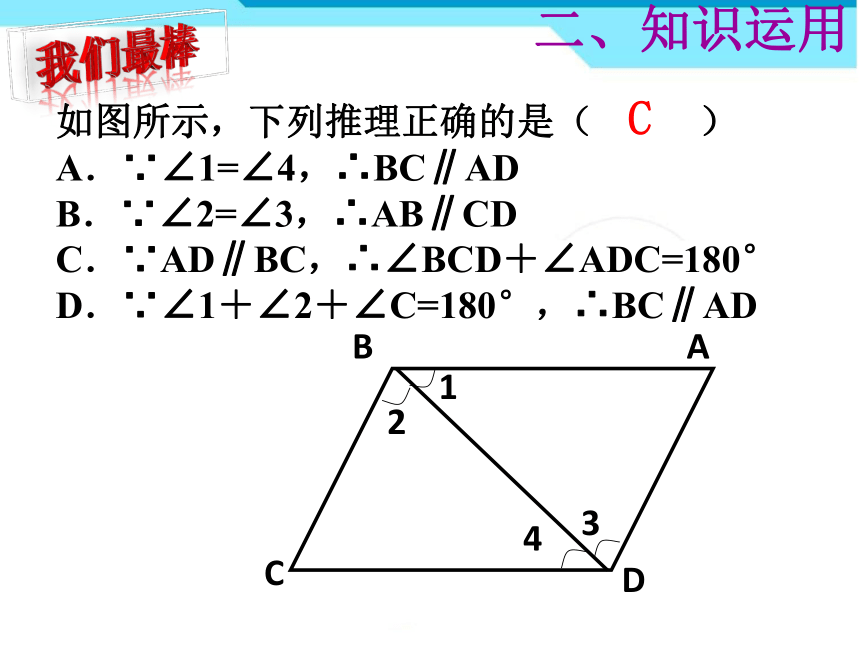
如图所示,下列推理正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AD∥BC,∴∠BCD+∠ADC=180°
D.∵∠1+∠2+∠C=180°,∴BC∥AD
2
4
B
C
1
3
A
D
我们最棒
C
二、知识运用
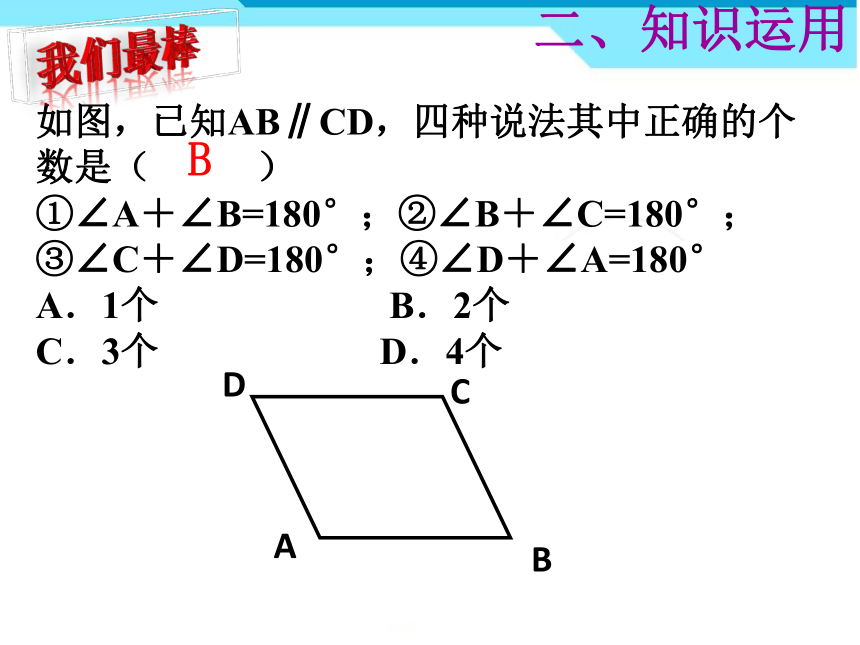
如图,已知AB∥CD,四种说法其中正确的个数是( )
①∠A+∠B=180°;②∠B+∠C=180°;
③∠C+∠D=180°;④∠D+∠A=180°
A.1个 B.2个
C.3个 D.4个
C
D
B
A
我们最棒
B
二、知识运用
(变式训练一)如图,AB∥CD,AD∥BC,试探求∠B与∠D,∠A与∠C的关系?
C
D
B
A
(变式训练二)如果AB∥CD,且∠B=∠D,你能推理得出AD∥BC吗?
我们最棒
三、知识拓展
我们最棒
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
解:
∵ AD//BC(已知)
∴ ∠A=∠ABF
(两直线平行,内错角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠C
(等量代换)
∴ AB∥DC
(同位角相等,两直线平行)
A
E
D
F
B
C
三、知识拓展
我们最棒
思考1:如图所示:AD∥BC,∠A=∠C,
试说明 AB∥DC .
AD∥BC.
AB∥DC,
证明
∵ AB//DC(已知)
∴ ∠C=∠ABF
(两直线平行,同位角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠A(等量代换)
∴ AD∥BC
(内错角相等,两直线平行)
A
E
D
F
B
C
三、知识拓展
三、合作释疑
证明
∴ ∠2=∠3(等量代换)
又∵∠C=∠D (已知)
∴ ∠D=∠ABD (等量代换)
∴ DF∥AC(内错角相等,两直线平行)
思考2:如图,点E为DF上的点,点B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC
3
2
1
D
E
F
A
B
C
∵∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
∴ BD∥CE(同位角相等,两直线平行)
∴ ∠C=∠ABD(两直线平行,同位角相等)
我们最棒
三、合作释疑
我们最棒
解:
∴ ∠2=∠3(等量代换)
又∵∠C=∠D (已知)
∴ ∠D=∠ABD (等量代换)
∴ DF∥AC(内错角相等,两直线平行)
思考3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
3
2
1
D
E
F
A
B
C
∵∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
∴ BD∥CE(同位角相等,两直线平行)
∴ ∠C=∠ABD(两直线平行,同位角相等)
∴ ∠A=∠F(两直线平行,内错角相等)
∠A与∠F 理由如下:
我们最棒
证明
又∵∠C=∠D (已知)
∴ ∠D=∠ABD
(两直线平行,内错角相等)
∴ BD∥CE(同位角相等,两直线平行)
思考4:如图,已知∠A=∠F,∠C=∠D,
求证:BD//CE.
3
2
1
D
E
F
A
B
C
∴ ∠C=∠ABD(等量代换)
∵∠A=∠F(已知)
∴ DF∥AC(内错角相等,两直线平行)
三、知识拓展
四、总结评价目标再现1.巩固平行线的判定与性质;2.灵活运用平行线判定与性质解决问题。3.初步学习证明过程四、总结评价
谈谈你对本节课的收获!
五、当堂检测
必做题
解:
∴ ∠BAD=∠ADC
(两直线平行,内错角相等)
又∵∠1=∠2 (已知)
∴ ∠E=∠F(两直线平行,内错角相等)
∵AB∥CD(已知)
∴ AF∥DE(内错角相等,两直线平行)
∴ ∠3=∠4(等式的性质)
如图,已知AB∥CD, ∠1=∠2,求证∠E=∠F.
F
1
E
D
B
A
2
C
)
(
3
4
选做题
五、当堂检测
思考1:如图,已知∠E=∠F, ∠1=∠2,
求证 AB∥CD .
F
1
E
D
B
A
2
C
)
(
3
4
思考2:如图,已知AB∥CD, ∠E=∠F,
求证∠1=∠2.
五、当堂检测
思考题
思考3:如图,已知AB∥CD, AF∥DE,
求证∠1=∠2.
思考4:如图,已知∠1=∠2, AF∥DE,
求证AB∥CD.
F
1
E
D
B
A
2
C
)
(
3
4
祝同学们学习进步!祝同学们学习进步!
5.3.4平行线的判定与性质义务教育教科书 数学 七年级 下册一、知识梳理
两直线平行
{
1.同位角相等
2.内错角相等
3.同旁内角互补
性质
判定
1.由_________得到___________的结论是平行线的判定;
请注意:
2.由____________得到______________的结论是平行线的性质.
用途:
用途:
角的关系
两直线平行
证明直线平行
两直线平行
角相等或互补
证明角相等或互补
学习目标1.巩固平行线的判定与性质;2.灵活运用平行线判定与性质解决问题。3.初步学习证明过程一、知识梳理二、知识运用
A
B
C
D
E
F
1
2
3
填空:
(1)、∵ ∠A=____, (已知)
∴ AC∥ED ,(_____________________ )
2、 ∵AB ∥______, (已知)
∴ ∠2= ∠4,(______________________)
3、 ∵ ___ ∥___, (已知)
∴ ∠B= ∠3. (___________ ___________)
4
5
∠4
同位角相等,两直线平行。
DF
两直线平行, 内错角相等。
AB
DF
两直线平行, 同位角相等.
判定
性质
性质
我们最棒
如图所示,下列推理正确的是( )
A.∵∠1=∠4,∴BC∥AD
B.∵∠2=∠3,∴AB∥CD
C.∵AD∥BC,∴∠BCD+∠ADC=180°
D.∵∠1+∠2+∠C=180°,∴BC∥AD
2
4
B
C
1
3
A
D
我们最棒
C
二、知识运用
如图,已知AB∥CD,四种说法其中正确的个数是( )
①∠A+∠B=180°;②∠B+∠C=180°;
③∠C+∠D=180°;④∠D+∠A=180°
A.1个 B.2个
C.3个 D.4个
C
D
B
A
我们最棒
B
二、知识运用
(变式训练一)如图,AB∥CD,AD∥BC,试探求∠B与∠D,∠A与∠C的关系?
C
D
B
A
(变式训练二)如果AB∥CD,且∠B=∠D,你能推理得出AD∥BC吗?
我们最棒
三、知识拓展
我们最棒
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
解:
∵ AD//BC(已知)
∴ ∠A=∠ABF
(两直线平行,内错角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠C
(等量代换)
∴ AB∥DC
(同位角相等,两直线平行)
A
E
D
F
B
C
三、知识拓展
我们最棒
思考1:如图所示:AD∥BC,∠A=∠C,
试说明 AB∥DC .
AD∥BC.
AB∥DC,
证明
∵ AB//DC(已知)
∴ ∠C=∠ABF
(两直线平行,同位角相等)
又∵∠A=∠C (已知)
∴ ∠ABF=∠A(等量代换)
∴ AD∥BC
(内错角相等,两直线平行)
A
E
D
F
B
C
三、知识拓展
三、合作释疑
证明
∴ ∠2=∠3(等量代换)
又∵∠C=∠D (已知)
∴ ∠D=∠ABD (等量代换)
∴ DF∥AC(内错角相等,两直线平行)
思考2:如图,点E为DF上的点,点B为AC上的点,
∠1= ∠2, ∠C= ∠D,求证:DF ∥AC
3
2
1
D
E
F
A
B
C
∵∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
∴ BD∥CE(同位角相等,两直线平行)
∴ ∠C=∠ABD(两直线平行,同位角相等)
我们最棒
三、合作释疑
我们最棒
解:
∴ ∠2=∠3(等量代换)
又∵∠C=∠D (已知)
∴ ∠D=∠ABD (等量代换)
∴ DF∥AC(内错角相等,两直线平行)
思考3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
3
2
1
D
E
F
A
B
C
∵∠1=∠2 (已知)
∠1=∠3 (对顶角相等)
∴ BD∥CE(同位角相等,两直线平行)
∴ ∠C=∠ABD(两直线平行,同位角相等)
∴ ∠A=∠F(两直线平行,内错角相等)
∠A与∠F 理由如下:
我们最棒
证明
又∵∠C=∠D (已知)
∴ ∠D=∠ABD
(两直线平行,内错角相等)
∴ BD∥CE(同位角相等,两直线平行)
思考4:如图,已知∠A=∠F,∠C=∠D,
求证:BD//CE.
3
2
1
D
E
F
A
B
C
∴ ∠C=∠ABD(等量代换)
∵∠A=∠F(已知)
∴ DF∥AC(内错角相等,两直线平行)
三、知识拓展
四、总结评价目标再现1.巩固平行线的判定与性质;2.灵活运用平行线判定与性质解决问题。3.初步学习证明过程四、总结评价
谈谈你对本节课的收获!
五、当堂检测
必做题
解:
∴ ∠BAD=∠ADC
(两直线平行,内错角相等)
又∵∠1=∠2 (已知)
∴ ∠E=∠F(两直线平行,内错角相等)
∵AB∥CD(已知)
∴ AF∥DE(内错角相等,两直线平行)
∴ ∠3=∠4(等式的性质)
如图,已知AB∥CD, ∠1=∠2,求证∠E=∠F.
F
1
E
D
B
A
2
C
)
(
3
4
选做题
五、当堂检测
思考1:如图,已知∠E=∠F, ∠1=∠2,
求证 AB∥CD .
F
1
E
D
B
A
2
C
)
(
3
4
思考2:如图,已知AB∥CD, ∠E=∠F,
求证∠1=∠2.
五、当堂检测
思考题
思考3:如图,已知AB∥CD, AF∥DE,
求证∠1=∠2.
思考4:如图,已知∠1=∠2, AF∥DE,
求证AB∥CD.
F
1
E
D
B
A
2
C
)
(
3
4
祝同学们学习进步!祝同学们学习进步!
