2021-2022学年人教版数学七年级下册 6.2 立方根 课件(共18张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册 6.2 立方根 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览






文档简介
6.2 立方根
学习目标:
1.了解立方根的概念和表示方法,并会求一个数的立方根;
2.从具体的计算出发归纳出立方根的概念,然后讨论立方与开立方的关系,研究立方根的特征。
3.通过探索立方根的特征,培养学生独立思考和小组交流的能力;通过立方根与平方根的比较使学生学会类比学习的数学思想;通过探讨一个数的立方根与它的相反数的立方根的关系,可以将求负数的立方根转化为求正数的立方根的问题,培养学生的转化思想。
教学重点:立方根的概念和求法
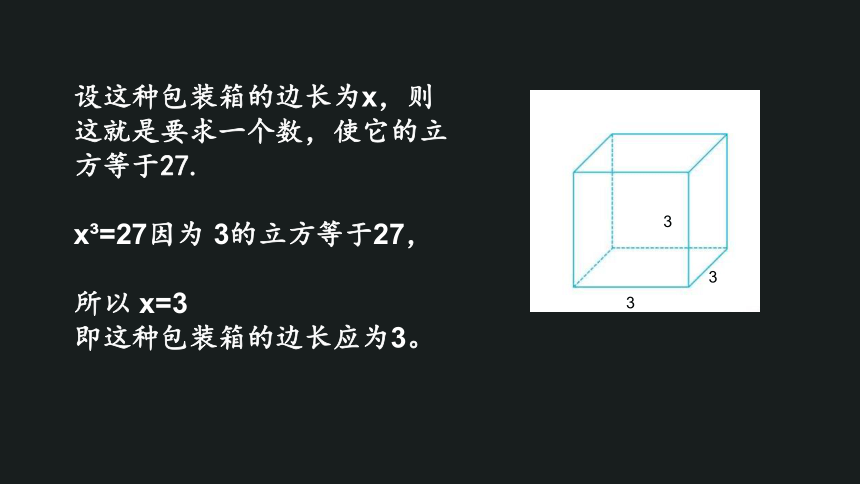
要制作一种容积为27的正方体形状的包装箱,这种包装箱的边长应该是多少?
设这种包装箱的边长为x,则这就是要求一个数,使它的立方等于27.
x?=27因为 3的立方等于27,
所以 x=3
即这种包装箱的边长应为3。
3
3
3
1.概念:
一般地,如果一个数的立方等于a,那么这个数叫做的a立方根或三次方根。
2.表示方法:
如果x?=a,那么x叫做的a立方根。记作????????,读作三次根号a。其中是a被开方数,3是根指数,????????中的根指数3不能省略。
?
求一个数的立方根的运算,叫做开立方。
开立方与立方互为逆运算,可以根据这种关系求一个数的立方根。
3.开立方的概念:
例:
????????????=???? ?????=????????
?
根据立方根的意义填空,思考正数、0、负数的立方根各有什么特点?
4、探索立方根的特点:
(1)因为 2?=8 ,所以8的立方根是( );
(2)因为 0.5?=0.125 ,0.125 所以的立方根是( ) ;
(3)因为 0?=0 ,0所以0的立方根是( );
(4)因为 (-2)?=-8 ,-8所以 的立方根是( );
(5)因为 (-4)?=-64 ,-64所以的立方根是( )。
2
0.5
0
-2
-4
1.正数的立方根是正数;
2.负数的立方根是负数;
3.0的立方根是0.
5.归纳:
例子:
(1)( )3=0.001; (2)( )3=-64; (3)( )3=0;
0.1
-4
0
不论正数、负数还是零,都有立方根!
6.牢记于心:
6?=216
7?=343
8?=512
9?=729
10?=1000
1?=1
2?=8
3?=27
4?=64
5?=125
例1. 已知x-2的平方根是±2,2x+y+7的立方根是3,求 的算术平方根.
x2+y2
解:∵x-2的平方根是±2,
∴x-2=4,
∴x=6.
∵2x+y+7的立方根是3,
∴2x+y+7=27.
把x=6代入解得y=8,
∴x2+y2=62+82=100.
∴x2+y2的算术平方根为10.
例2:
(1)?3343= (2)32764=
?
(1)∵7的立方是343
∴三次根号343等于7,然后再相反数
∴?3343=7
?
(2) ∵34的立方是2764
∴三次根号2764等于34 ∴32764=34
?
7.课堂练习:
(1).-8的立方根是( ) A.-2 B.±2 C.2 D.12
?
(2)-64的立方根是__________
(3)- 13是__________的立方根.
?
A
-4
-127
?
(4).下列说法正确的是( ) A.如果一个数的立方根是这个数本身,那么这个数一定是0 B.一个数的立方根不是正数就是负数 C.负数没有立方根 D.一个不为零的数的立方根和这个数同号,0的立方根是0
D
(5).下列说法正确的是( ) A.一个数的立方根有两个,它们互为相反数 B.一个数的立方根比这个数平方根小 C.如果一个数有立方根,那么它一定有平方根
D.一个数的立方根可正可负可为零
D
(6).正方体A的体积是正方体B的体积的27倍,那么正方体A的棱长是正方体B的棱长的( )A.2倍 B.3倍 C.4倍 D.5倍
B
(7).求下列各式中的x: (1)8x3+125=0; (2)(x+3)3+27=0.
(8).比较下列各组数的大小.
(1) 与2.5; (2) 与 .
谢谢观看!再见!
学习目标:
1.了解立方根的概念和表示方法,并会求一个数的立方根;
2.从具体的计算出发归纳出立方根的概念,然后讨论立方与开立方的关系,研究立方根的特征。
3.通过探索立方根的特征,培养学生独立思考和小组交流的能力;通过立方根与平方根的比较使学生学会类比学习的数学思想;通过探讨一个数的立方根与它的相反数的立方根的关系,可以将求负数的立方根转化为求正数的立方根的问题,培养学生的转化思想。
教学重点:立方根的概念和求法
要制作一种容积为27的正方体形状的包装箱,这种包装箱的边长应该是多少?
设这种包装箱的边长为x,则这就是要求一个数,使它的立方等于27.
x?=27因为 3的立方等于27,
所以 x=3
即这种包装箱的边长应为3。
3
3
3
1.概念:
一般地,如果一个数的立方等于a,那么这个数叫做的a立方根或三次方根。
2.表示方法:
如果x?=a,那么x叫做的a立方根。记作????????,读作三次根号a。其中是a被开方数,3是根指数,????????中的根指数3不能省略。
?
求一个数的立方根的运算,叫做开立方。
开立方与立方互为逆运算,可以根据这种关系求一个数的立方根。
3.开立方的概念:
例:
????????????=???? ?????=????????
?
根据立方根的意义填空,思考正数、0、负数的立方根各有什么特点?
4、探索立方根的特点:
(1)因为 2?=8 ,所以8的立方根是( );
(2)因为 0.5?=0.125 ,0.125 所以的立方根是( ) ;
(3)因为 0?=0 ,0所以0的立方根是( );
(4)因为 (-2)?=-8 ,-8所以 的立方根是( );
(5)因为 (-4)?=-64 ,-64所以的立方根是( )。
2
0.5
0
-2
-4
1.正数的立方根是正数;
2.负数的立方根是负数;
3.0的立方根是0.
5.归纳:
例子:
(1)( )3=0.001; (2)( )3=-64; (3)( )3=0;
0.1
-4
0
不论正数、负数还是零,都有立方根!
6.牢记于心:
6?=216
7?=343
8?=512
9?=729
10?=1000
1?=1
2?=8
3?=27
4?=64
5?=125
例1. 已知x-2的平方根是±2,2x+y+7的立方根是3,求 的算术平方根.
x2+y2
解:∵x-2的平方根是±2,
∴x-2=4,
∴x=6.
∵2x+y+7的立方根是3,
∴2x+y+7=27.
把x=6代入解得y=8,
∴x2+y2=62+82=100.
∴x2+y2的算术平方根为10.
例2:
(1)?3343= (2)32764=
?
(1)∵7的立方是343
∴三次根号343等于7,然后再相反数
∴?3343=7
?
(2) ∵34的立方是2764
∴三次根号2764等于34 ∴32764=34
?
7.课堂练习:
(1).-8的立方根是( ) A.-2 B.±2 C.2 D.12
?
(2)-64的立方根是__________
(3)- 13是__________的立方根.
?
A
-4
-127
?
(4).下列说法正确的是( ) A.如果一个数的立方根是这个数本身,那么这个数一定是0 B.一个数的立方根不是正数就是负数 C.负数没有立方根 D.一个不为零的数的立方根和这个数同号,0的立方根是0
D
(5).下列说法正确的是( ) A.一个数的立方根有两个,它们互为相反数 B.一个数的立方根比这个数平方根小 C.如果一个数有立方根,那么它一定有平方根
D.一个数的立方根可正可负可为零
D
(6).正方体A的体积是正方体B的体积的27倍,那么正方体A的棱长是正方体B的棱长的( )A.2倍 B.3倍 C.4倍 D.5倍
B
(7).求下列各式中的x: (1)8x3+125=0; (2)(x+3)3+27=0.
(8).比较下列各组数的大小.
(1) 与2.5; (2) 与 .
谢谢观看!再见!
