2021-2022学年人教版七年级数学下册5.2.2平行线性质课件(16张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线性质课件(16张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 13:58:07 | ||
图片预览






文档简介
(共16张PPT)
5.2.2平行线的性质
1、了解并掌握平行线的性质,并能利用平行线的性质进行相关的数学计算。
2、能够区分平行线的性质和判定,能够利用平行线的性质进行简单的逻辑推理。
3.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
学习目标:
问题探究
01
02
平行线性质一
03
平行线性质二
04
平行线性质三
目录
如图,工人在修一条高速公路时遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯是左拐30,那么第二个弯应朝什么方向。
一.问题探究:
a
b
1
2
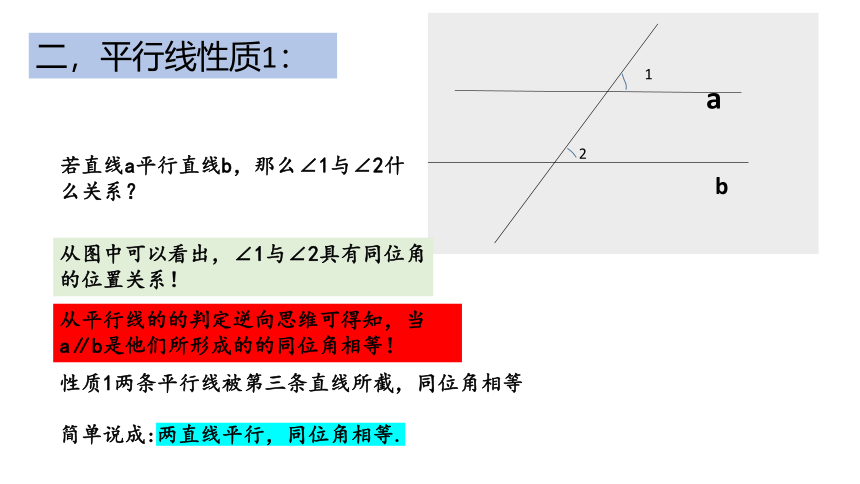
二,平行线性质1:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有同位角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的同位角相等!
性质1两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等.
你能根据性质1,说出性质2,性质3成立的理由吗?
如图,因为a∥b.
所以 ∠1=∠2(两直线平行同位角相当)又∠3=∠2,(对顶角相等)所以∠2=∠3,
类似地,对于性质3,你能说出道理吗?
1
2
3
a
b
1
2
平行线性质2:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有内错角角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的内错角相等!
性质1两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等.
a
b
1
2
平行线性质3:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有同旁内角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的同旁内角互补!
性质1两条平行线被第三条直线所截,同旁内角互补!
简单说成:两直线平行,同旁内角互补.
三,练习天地:
1. 下列命题正确的是 ( )A.两直线与第三条直线相交,同位角相等
B.两直线与第三条直线相交,内错角相等
C.两直线平行,内错角相等
D.两直线平行,同旁内角相等
答案:C 本题考查了平行线的性质 根据平行线的性质依次判断即可。 A、缺少两直线平行的前提,故本选项错误;
B、缺少两直线平行的前提,故本选项错误;
C、两直线平行,内错角相等,正确;
D、两直线平行,同旁内角应该互补,故本选项错误; 故选C.
2. 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
A.23° B.22° C.37° D.67°
答案:C
解析:∵直尺的两边互相平行,∠1=23°,
∴∠3=∠1=23°, ∴∠2=60°-∠3=60°-23°=37°.
故选 C.
考点:平行线的性质.
3.如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为( )
A.20° B.70°
C.100° D.110°
答案:D.
解析:根据邻补角的性质可得∠ABC的度数,再根据两直线平行内错角相等可得答案:
∵∠ABE=70°,
∴∠ABC=180°-70°=110°.
∵AB∥CD,
∴∠ECD=∠ABC=110°. 故选 D.
4.如图,AB=AC, AD∥BC,∠BAC=100°,则∠CAD的度数是( )
A.30° B.35° C.40° D.50°
答案: C. 解析:根据等腰三角形性质,三角形内角和定理求出∠C,根据平行线的性质得出∠CAD=∠C,即可求出答案: ∵AB=AC,∠BAC=100°,∴∠B=∠C=40°. ∵AD∥BC,∴∠CAD=∠C=40°. 故选 C. 考点:1.平行线的性质;2.等腰三角形的性质.
5. 如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于( )
A.30° B.45°
C.60° D.75°
答案: D.
解析:过E作EF∥AC,如图:
∵AC∥BD,
∴EF∥BD,
∴∠B=∠2=45°,
∵AC∥EF,
∴∠1=∠A=30°, ∴∠AEB=30°+45°=75°, 故选 D. 考点:平行线的性质.
6. 如图,点D是△ABC的边AB的延长线上一点,BE∥AC, 若∠C=50°,∠DBE=60°,则∠CBD的度数等于 A.120° B.110° C.100° D.70°
答案: B.
解析:∵BE∥AC,
∴∠CBE=∠C
而∠C=50°
∴∠CBE=50°
又∠DBE=60°
∴∠CBD=∠CBE+∠DBE=50°+60°=110°.
故选B.
考点:平行线的性质.
18. 如图,已知∠B=∠C,AD∥BC,
求证:AD平分∠CAE.
解析:利用两直线平行,同位角相等和角平分线的定义进行即可.
∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等) ∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义).
考点:1,平行线的性质2.角平分线的定义.
2022
再见!
谢谢观看!
5.2.2平行线的性质
1、了解并掌握平行线的性质,并能利用平行线的性质进行相关的数学计算。
2、能够区分平行线的性质和判定,能够利用平行线的性质进行简单的逻辑推理。
3.经历探索直线平行的性质的过程,掌握平行线的三条性质,并能用它们进行简单的推理和计算。
学习目标:
问题探究
01
02
平行线性质一
03
平行线性质二
04
平行线性质三
目录
如图,工人在修一条高速公路时遇到一座高山,为了降低施工难度,工程师决定绕过这座山,如果第一个弯是左拐30,那么第二个弯应朝什么方向。
一.问题探究:
a
b
1
2
二,平行线性质1:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有同位角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的同位角相等!
性质1两条平行线被第三条直线所截,同位角相等
简单说成:两直线平行,同位角相等.
你能根据性质1,说出性质2,性质3成立的理由吗?
如图,因为a∥b.
所以 ∠1=∠2(两直线平行同位角相当)又∠3=∠2,(对顶角相等)所以∠2=∠3,
类似地,对于性质3,你能说出道理吗?
1
2
3
a
b
1
2
平行线性质2:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有内错角角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的内错角相等!
性质1两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等.
a
b
1
2
平行线性质3:
若直线a平行直线b,那么∠1与∠2什么关系?
从图中可以看出,∠1与∠2具有同旁内角的位置关系!
从平行线的的判定逆向思维可得知,当a∥b是他们所形成的的同旁内角互补!
性质1两条平行线被第三条直线所截,同旁内角互补!
简单说成:两直线平行,同旁内角互补.
三,练习天地:
1. 下列命题正确的是 ( )A.两直线与第三条直线相交,同位角相等
B.两直线与第三条直线相交,内错角相等
C.两直线平行,内错角相等
D.两直线平行,同旁内角相等
答案:C 本题考查了平行线的性质 根据平行线的性质依次判断即可。 A、缺少两直线平行的前提,故本选项错误;
B、缺少两直线平行的前提,故本选项错误;
C、两直线平行,内错角相等,正确;
D、两直线平行,同旁内角应该互补,故本选项错误; 故选C.
2. 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
A.23° B.22° C.37° D.67°
答案:C
解析:∵直尺的两边互相平行,∠1=23°,
∴∠3=∠1=23°, ∴∠2=60°-∠3=60°-23°=37°.
故选 C.
考点:平行线的性质.
3.如图所示,AB∥CD,点E在CB的延长线上.若∠ABE=70°,则∠ECD的度数为( )
A.20° B.70°
C.100° D.110°
答案:D.
解析:根据邻补角的性质可得∠ABC的度数,再根据两直线平行内错角相等可得答案:
∵∠ABE=70°,
∴∠ABC=180°-70°=110°.
∵AB∥CD,
∴∠ECD=∠ABC=110°. 故选 D.
4.如图,AB=AC, AD∥BC,∠BAC=100°,则∠CAD的度数是( )
A.30° B.35° C.40° D.50°
答案: C. 解析:根据等腰三角形性质,三角形内角和定理求出∠C,根据平行线的性质得出∠CAD=∠C,即可求出答案: ∵AB=AC,∠BAC=100°,∴∠B=∠C=40°. ∵AD∥BC,∴∠CAD=∠C=40°. 故选 C. 考点:1.平行线的性质;2.等腰三角形的性质.
5. 如图,已知AC∥BD,∠CAE=30°,∠DBE=45°,则∠AEB等于( )
A.30° B.45°
C.60° D.75°
答案: D.
解析:过E作EF∥AC,如图:
∵AC∥BD,
∴EF∥BD,
∴∠B=∠2=45°,
∵AC∥EF,
∴∠1=∠A=30°, ∴∠AEB=30°+45°=75°, 故选 D. 考点:平行线的性质.
6. 如图,点D是△ABC的边AB的延长线上一点,BE∥AC, 若∠C=50°,∠DBE=60°,则∠CBD的度数等于 A.120° B.110° C.100° D.70°
答案: B.
解析:∵BE∥AC,
∴∠CBE=∠C
而∠C=50°
∴∠CBE=50°
又∠DBE=60°
∴∠CBD=∠CBE+∠DBE=50°+60°=110°.
故选B.
考点:平行线的性质.
18. 如图,已知∠B=∠C,AD∥BC,
求证:AD平分∠CAE.
解析:利用两直线平行,同位角相等和角平分线的定义进行即可.
∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等) ∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义).
考点:1,平行线的性质2.角平分线的定义.
2022
再见!
谢谢观看!
