2021-2022学年人教版七年级数学下册8.1二元一次方程组课件(20张)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册8.1二元一次方程组课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第八章
二元一次方程组
学习目标
1.了解二元一次方程,二元一次方程组及其解等概念,并会判断一组数是不是某个二元一次方程组的解.
2.通过对实际问题的分析,进一步体会方程是刻画现实世界数量关系的有效数学模型.
3.通过对实际问题的分析及解决,学会用多种方法解决问题,培养学生的创新意识.
4.实际生活与数学息息相关,存在紧密的联系,增强学生学习数学的兴趣.
二元一次方程组
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
NBA选秀中,首位非美籍状元是谁?
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
他所在的NBA球队是哪支?
火箭队
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
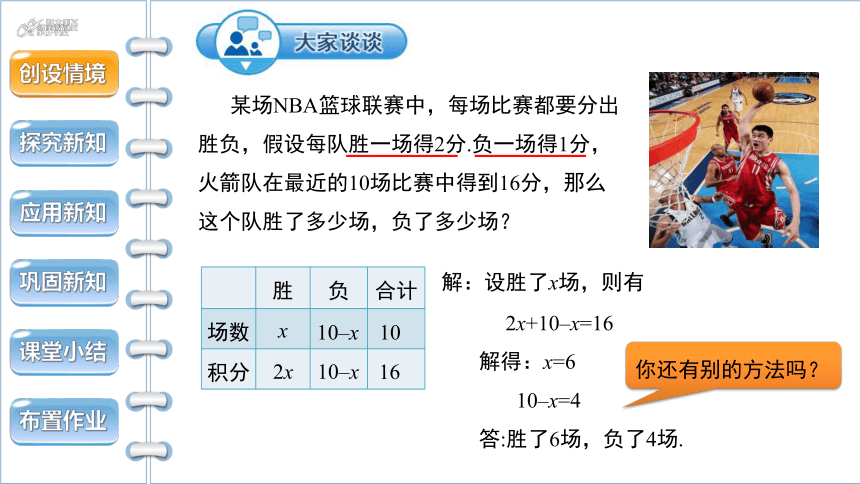
某场NBA篮球联赛中,每场比赛都要分出胜负,假设每队胜一场得2分.负一场得1分,火箭队在最近的10场比赛中得到16分,那么这个队胜了多少场,负了多少场?
解:设胜了x场,则有
胜 负 合计
场数
积分
2x+10–x=16
解得:x=6
10–x=4
答:胜了6场,负了4场.
x
10
10–x
2x
10–x
16
你还有别的方法吗?
这个问题中包含了哪些必须同时满足的条件?
胜 负 合计
场数 x 10–x 10
积分 2x 10–x 16
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如果设胜的场数是x,负的场数是y,你能用
方程把这些条件表示出来吗?
胜 负 合计
场数 10
积分 16
x
y
2x
y
胜场积分+负场积分=总积分
2x+y=16
胜的场数+负的场数=总场数
x+y=10
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面我们列出的方程有什么特征呢?
x+y=10
2x+y=16
含有两个未知数
未知数的最高次数为1
二元一次方程
含有两个未知数,并且含有未知数的项的最高次数为1的方程叫二元一次方程.
1
1
1
1
二元
一次
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面的问题中未知数x,y必须同时满足方程
x+y=10
2x+y=16
二元一次方程组
二元一次方程组
这个方程组中有两个未知数,含有未知数的项的最高次数为1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面我们提到的二元一次方程,同学们可以找出符合实际要求的x和y的值吗?
x+y=10 ①
x
y
观察上表,你发现了什么?
x=0,y=10;x=1,y=9;使方程x+y=10两边的值相等
二元一次方程的解
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
0
10
1
9
2
8
3
7
4
6
5
5
6
4
7
3
8
2
9
1
10
0
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
你能再找出第二个方程中符合实际要求的x和y的值吗?填写下表:
2x+y=16 ②
x
y
0
16
1
14
2
12
3
10
4
8
5
6
6
4
7
2
8
0
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
2x+y=16 ②
x 0 1 2 3 4 5 6 7 8
y 16 14 12 10 8 6 4 2 0
x+y=10 ①
x 0 1 2 3 4 5 6 7 8 9 10
y 10 9 8 7 6 5 4 3 2 1 0
观察这两个表,你发现了什么?
x=6,y=4是方程①与方程②的公共解.
x=6,y=4叫做二元一次方程组 的解.
记作:
二元一次方程组的解
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1:有下列方程组:
①
①
②
③
④
⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
1.含有两个未知数
2.未知数的最高次数为1
3.整式方程
B
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例2:下列四组数值中,哪个不是二元一次方程x–3y=1的解( )
①
A. B. C. D.
A.
A.将x=2,y=3代入x–3y=1,得:2–9= –7≠1,不是
B.将x=4,y=1代入x–3y=1,得:4–3=1,是
C.将x=10,y=3代入x–3y=1,得:10–9=1,是
D.将x= –5,y=–2代入x–3y=1,得: –5+6=1,是
A
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例3:以 为解的二元一次方程组是( )
①
A. B. C. D.
A.
将x=1,y=2分别代入A、B、C、D选项,得
A中1–2= –1≠3,不是
B中3+2=5≠ –5,不是
C中3+10=13≠ –5 ,不是
D中1–2= –1,3+2=5都成立,是
D
随堂练习
1.下列各组值中是二元一次方程组 的解的是( )
C
2.已知 是二元一次方程组 的解,
则m-n的值是 .
4
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
3.火箭队为了在NBA联赛中取得优异的成绩,平时特别注意队员的训练,每人每天投射300个2分球,或200个3分球,现有10个队员参加投球训练,应如何安排才能使投2分球和投3分球的数量相等?
解:设投2分球的队员安排x名,投3分球的队员安排y名;则
是 的解吗?
是
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
二元一次方程(组)的概念
二元一次方程(组)的解
含有两个未知数,并且含有未知数的项的最高次数为1的方程叫二元一次方程.
有两个未知数,含有未知数的项的最高次数为1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
二元一次方程组
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
布置作业
教科书P90
练习1-4
探究新知
应用新知
课堂小结
巩固新知
创设情境
再 见
第八章
二元一次方程组
学习目标
1.了解二元一次方程,二元一次方程组及其解等概念,并会判断一组数是不是某个二元一次方程组的解.
2.通过对实际问题的分析,进一步体会方程是刻画现实世界数量关系的有效数学模型.
3.通过对实际问题的分析及解决,学会用多种方法解决问题,培养学生的创新意识.
4.实际生活与数学息息相关,存在紧密的联系,增强学生学习数学的兴趣.
二元一次方程组
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
NBA选秀中,首位非美籍状元是谁?
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
他所在的NBA球队是哪支?
火箭队
应用新知
创设情境
巩固新知
课堂小结
布置作业
探究新知
某场NBA篮球联赛中,每场比赛都要分出胜负,假设每队胜一场得2分.负一场得1分,火箭队在最近的10场比赛中得到16分,那么这个队胜了多少场,负了多少场?
解:设胜了x场,则有
胜 负 合计
场数
积分
2x+10–x=16
解得:x=6
10–x=4
答:胜了6场,负了4场.
x
10
10–x
2x
10–x
16
你还有别的方法吗?
这个问题中包含了哪些必须同时满足的条件?
胜 负 合计
场数 x 10–x 10
积分 2x 10–x 16
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
如果设胜的场数是x,负的场数是y,你能用
方程把这些条件表示出来吗?
胜 负 合计
场数 10
积分 16
x
y
2x
y
胜场积分+负场积分=总积分
2x+y=16
胜的场数+负的场数=总场数
x+y=10
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面我们列出的方程有什么特征呢?
x+y=10
2x+y=16
含有两个未知数
未知数的最高次数为1
二元一次方程
含有两个未知数,并且含有未知数的项的最高次数为1的方程叫二元一次方程.
1
1
1
1
二元
一次
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面的问题中未知数x,y必须同时满足方程
x+y=10
2x+y=16
二元一次方程组
二元一次方程组
这个方程组中有两个未知数,含有未知数的项的最高次数为1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
上面我们提到的二元一次方程,同学们可以找出符合实际要求的x和y的值吗?
x+y=10 ①
x
y
观察上表,你发现了什么?
x=0,y=10;x=1,y=9;使方程x+y=10两边的值相等
二元一次方程的解
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
0
10
1
9
2
8
3
7
4
6
5
5
6
4
7
3
8
2
9
1
10
0
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
你能再找出第二个方程中符合实际要求的x和y的值吗?填写下表:
2x+y=16 ②
x
y
0
16
1
14
2
12
3
10
4
8
5
6
6
4
7
2
8
0
创设情境
应用新知
巩固新知
课堂小结
布置作业
探究新知
2x+y=16 ②
x 0 1 2 3 4 5 6 7 8
y 16 14 12 10 8 6 4 2 0
x+y=10 ①
x 0 1 2 3 4 5 6 7 8 9 10
y 10 9 8 7 6 5 4 3 2 1 0
观察这两个表,你发现了什么?
x=6,y=4是方程①与方程②的公共解.
x=6,y=4叫做二元一次方程组 的解.
记作:
二元一次方程组的解
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例1:有下列方程组:
①
①
②
③
④
⑤
其中二元一次方程组有( )
A.1个 B.2个 C.3个 D.4个
1.含有两个未知数
2.未知数的最高次数为1
3.整式方程
B
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例2:下列四组数值中,哪个不是二元一次方程x–3y=1的解( )
①
A. B. C. D.
A.
A.将x=2,y=3代入x–3y=1,得:2–9= –7≠1,不是
B.将x=4,y=1代入x–3y=1,得:4–3=1,是
C.将x=10,y=3代入x–3y=1,得:10–9=1,是
D.将x= –5,y=–2代入x–3y=1,得: –5+6=1,是
A
探究新知
创设情境
巩固新知
课堂小结
布置作业
应用新知
例3:以 为解的二元一次方程组是( )
①
A. B. C. D.
A.
将x=1,y=2分别代入A、B、C、D选项,得
A中1–2= –1≠3,不是
B中3+2=5≠ –5,不是
C中3+10=13≠ –5 ,不是
D中1–2= –1,3+2=5都成立,是
D
随堂练习
1.下列各组值中是二元一次方程组 的解的是( )
C
2.已知 是二元一次方程组 的解,
则m-n的值是 .
4
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
3.火箭队为了在NBA联赛中取得优异的成绩,平时特别注意队员的训练,每人每天投射300个2分球,或200个3分球,现有10个队员参加投球训练,应如何安排才能使投2分球和投3分球的数量相等?
解:设投2分球的队员安排x名,投3分球的队员安排y名;则
是 的解吗?
是
随堂练习
探究新知
创设情境
应用新知
课堂小结
布置作业
巩固新知
二元一次方程(组)的概念
二元一次方程(组)的解
含有两个未知数,并且含有未知数的项的最高次数为1的方程叫二元一次方程.
有两个未知数,含有未知数的项的最高次数为1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
探究新知
应用新知
布置作业
巩固新知
课堂小结
创设情境
二元一次方程组
二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
布置作业
教科书P90
练习1-4
探究新知
应用新知
课堂小结
巩固新知
创设情境
再 见
