苏科版七年级数学下册 第7章 平面图形的认识(二) 教案
文档属性
| 名称 | 苏科版七年级数学下册 第7章 平面图形的认识(二) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览

文档简介
平行线复习
一、教学目标
1.复习巩固平行线的有关概念和性质,使学生会用这些概念或性质进行简单的推理或计算,并能在适当的时候借助于辅助线
2.通过对所学知识的回顾与整理,使学生对平行线的知识更加条理化、系统化,并能灵活运用
3.使学生进一步学会识图,能将复杂图形分解为基本图形,学会图形、符号语言、几何语言的转化。
二、重点、难点突破
重点:
平行线的条件与性质
1、平行线:在同一平面内,不相交的两条直线叫做平行线。
2、直线平行的条件:
(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
同旁内角相等,两直线平行。
3、平行线的性质:
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
4、平行线、角平分线、等腰三角形的基础题
5、平行线、翻折问题
难点:
(1)找同位角、内错角、同旁内角。
(2)能够运用平行的基础知识解题。
整合拓展创新
1.如图7-1,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
(
图7-2
)
(
图7-1
)
2按图7-2填空:(1)因为∠1=∠2,所以__∥__,理由是______,两直线平行.
(2)因为AD∥BC,所以 ∠D+_____=180°理由 是__________,
例1:下列说法中,不正确的是( )
A.两条平行直线被第三条直线所截,平行线的内错角的平分线互相平行
B.两条平行直线被第三条直线所截,平行线的同位角的平分线互相平行
C.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相平行
D.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相垂直
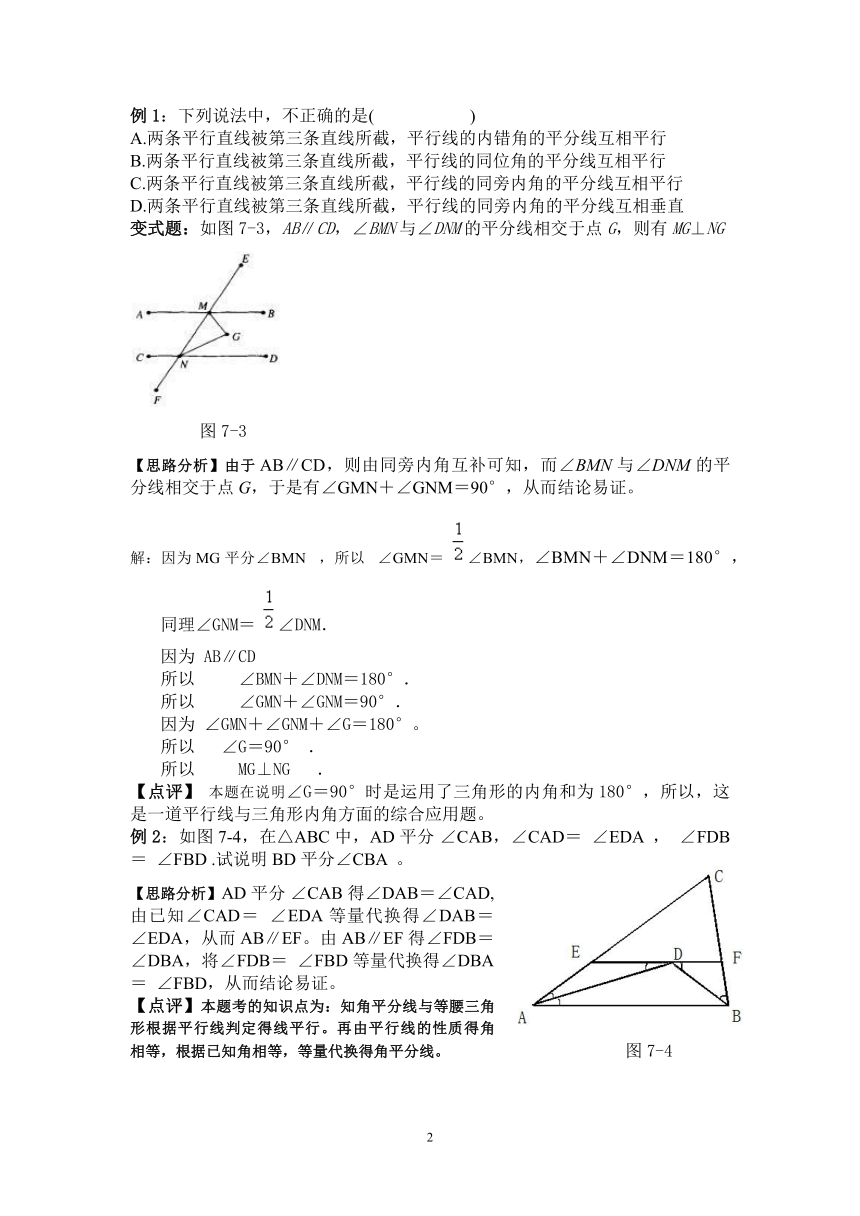
变式题:如图7-3,AB∥CD,∠BMN与∠DNM的平分线相交于点G,则有MG⊥NG
图7-3
【思路分析】由于AB∥CD,则由同旁内角互补可知,而∠BMN与∠DNM的平分线相交于点G,于是有∠GMN+∠GNM=90°,从而结论易证。
解:因为MG平分∠BMN ,所以 ∠GMN= ∠BMN,∠BMN+∠DNM=180°,
同理∠GNM= ∠DNM.
因为 AB∥CD
所以 ∠BMN+∠DNM=180°.
所以 ∠GMN+∠GNM=90°.
因为 ∠GMN+∠GNM+∠G=180°。
所以 ∠G=90° .
所以 MG⊥NG .
【点评】 本题在说明∠G=90°时是运用了三角形的内角和为180°,所以,这是一道平行线与三角形内角方面的综合应用题。
例2:如图7-4,在△ABC中,AD平分 ∠CAB,∠CAD= ∠EDA , ∠FDB= ∠FBD .试说明BD平分∠CBA 。
【思路分析】AD平分 ∠CAB得∠DAB=∠CAD,由已知∠CAD= ∠EDA等量代换得∠DAB=∠EDA,从而AB∥EF。由AB∥EF得∠FDB= ∠DBA,将∠FDB= ∠FBD等量代换得∠DBA= ∠FBD,从而结论易证。
【点评】本题考的知识点为:知角平分线与等腰三角形根据平行线判定得线平行。再由平行线的性质得角相等,根据已知角相等,等量代换得角平分线。 图7-4
例3:潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
潜望镜科普知识:
作用:处于水下航行状态的潜艇观察海平面和空中情况的唯一手段便是借助潜望镜。而多数潜艇均安装有两部潜望镜――一部攻击潜望镜和一部观察潜望镜。前者用于发现和瞄准水面目标,而后者主要用于观察海空情况和导航观测。潜艇在浮出水面前,艇长都必须指挥潜艇在潜望镜深度先用潜望镜对海平面作一次360度的观察,以求尽早发现可能出现的敌情。只有在确认没有任何威胁的情况下潜艇才会浮出水面。
缺陷:潜望镜升至指挥塔外5米高的位置,两端都安装有棱镜和透镜并可将潜望镜的视野放大至1X到6X。潜望镜的使用有两个很明显的问题:当潜望镜完全升起时,细长的潜望镜桅杆会影响潜艇的正常航行,造成横向的不稳定。另外一个重要问题是潜望镜镜片产生的雾气。由于潜艇内部空气潮湿,潜望镜的镜片多会产生雾气,所以潜望镜在设计制造时就必须尽量做到防水和密封。
【点评】激发学生学习的兴趣,体会数学源于生活,服务于生活。
例4:如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠1、∠2的度数。
练习:如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿GF折叠成图3,则图3中的∠CFE的度数是 °.
【点评】将折叠与平行线叠加,本质仍然是角平分线与平行线。
例5:如图7-5,已知DE⊥AC,BC⊥AC,FG⊥AB于G,∠1=∠2,则CD⊥AB,为什么?
【思路分析】
解:因为DE⊥AC BC⊥AC 所以DE//BC
所以∠2=∠DCB
又因为∠1=∠2 所以∠1=∠DCB
所以CD//GF
又因为GF⊥AB 所以CD⊥AB
【点评】实际上,在说明GF⊥AB时,也可从同位角或同旁内角的角度,这样,学生更易于接受。
例6 如图7-6,已知∠BED=∠B+∠D,则AB//CD,为什么?
7-6
【思路分析】要得到AB//CD,从已知条件看,只有作EF//AB或EF//CD,借助于已知条件,得出内错角相等,然后才有EF//CD或EF//AB。
法一:解:过E作EF//AB,则∠BED=∠BEF+∠FED
因为EF//AB所以∠BEF=∠B
于是∠BED=∠B+∠FED
又∠BED=∠B+∠D
所以∠FED=∠D所以EF//CD。
而EF//AB 所以AB//CD。
法二:延长BE交CD于点F
因为∠BED=∠B+∠D, ∠BED=∠EFD+∠D
所以∠B=∠EFD
所以AB//CD
【点评】本题主要是“两直线平行,内错角相等”的正、逆向运用。或三角形外角性质与平行线判定
变式题
已知:如图7-7,BE∥DF,∠B=∠D。求证:AD∥BC
【思路分析】 要说明AD∥BC,结合所给的条件:BE∥DF,∠B=∠D,则应从BE∥DF看,由它可得相关和角相等:∠D=∠EAD,再由∠B=∠D可得∠B=∠EAD。
解:因为BE∥DF,所以∠
D=∠EAD,
因为∠B=∠D,所以∠B=∠EAD,所以AD∥BC。
本课小结: 直线平行的条件; 平行线的性质; 平行线、角平分线、等腰三角形的基础题
作业布置
4
一、教学目标
1.复习巩固平行线的有关概念和性质,使学生会用这些概念或性质进行简单的推理或计算,并能在适当的时候借助于辅助线
2.通过对所学知识的回顾与整理,使学生对平行线的知识更加条理化、系统化,并能灵活运用
3.使学生进一步学会识图,能将复杂图形分解为基本图形,学会图形、符号语言、几何语言的转化。
二、重点、难点突破
重点:
平行线的条件与性质
1、平行线:在同一平面内,不相交的两条直线叫做平行线。
2、直线平行的条件:
(1)同位角相等,两直线平行。
(2)内错角相等,两直线平行。
同旁内角相等,两直线平行。
3、平行线的性质:
(1)两直线平行,同位角相等。
(2)两直线平行,内错角相等。
(3)两直线平行,同旁内角互补。
4、平行线、角平分线、等腰三角形的基础题
5、平行线、翻折问题
难点:
(1)找同位角、内错角、同旁内角。
(2)能够运用平行的基础知识解题。
整合拓展创新
1.如图7-1,∠1与∠B,∠3与∠4,∠2与∠4分别是哪两条直线被哪一条直线截成的角?它们分别是什么角?
(
图7-2
)
(
图7-1
)
2按图7-2填空:(1)因为∠1=∠2,所以__∥__,理由是______,两直线平行.
(2)因为AD∥BC,所以 ∠D+_____=180°理由 是__________,
例1:下列说法中,不正确的是( )
A.两条平行直线被第三条直线所截,平行线的内错角的平分线互相平行
B.两条平行直线被第三条直线所截,平行线的同位角的平分线互相平行
C.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相平行
D.两条平行直线被第三条直线所截,平行线的同旁内角的平分线互相垂直
变式题:如图7-3,AB∥CD,∠BMN与∠DNM的平分线相交于点G,则有MG⊥NG
图7-3
【思路分析】由于AB∥CD,则由同旁内角互补可知,而∠BMN与∠DNM的平分线相交于点G,于是有∠GMN+∠GNM=90°,从而结论易证。
解:因为MG平分∠BMN ,所以 ∠GMN= ∠BMN,∠BMN+∠DNM=180°,
同理∠GNM= ∠DNM.
因为 AB∥CD
所以 ∠BMN+∠DNM=180°.
所以 ∠GMN+∠GNM=90°.
因为 ∠GMN+∠GNM+∠G=180°。
所以 ∠G=90° .
所以 MG⊥NG .
【点评】 本题在说明∠G=90°时是运用了三角形的内角和为180°,所以,这是一道平行线与三角形内角方面的综合应用题。
例2:如图7-4,在△ABC中,AD平分 ∠CAB,∠CAD= ∠EDA , ∠FDB= ∠FBD .试说明BD平分∠CBA 。
【思路分析】AD平分 ∠CAB得∠DAB=∠CAD,由已知∠CAD= ∠EDA等量代换得∠DAB=∠EDA,从而AB∥EF。由AB∥EF得∠FDB= ∠DBA,将∠FDB= ∠FBD等量代换得∠DBA= ∠FBD,从而结论易证。
【点评】本题考的知识点为:知角平分线与等腰三角形根据平行线判定得线平行。再由平行线的性质得角相等,根据已知角相等,等量代换得角平分线。 图7-4
例3:潜望镜中的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2、∠3=∠4,请解释为什么进入潜望镜的光线与离开潜望镜的光线是互相平行的。
潜望镜科普知识:
作用:处于水下航行状态的潜艇观察海平面和空中情况的唯一手段便是借助潜望镜。而多数潜艇均安装有两部潜望镜――一部攻击潜望镜和一部观察潜望镜。前者用于发现和瞄准水面目标,而后者主要用于观察海空情况和导航观测。潜艇在浮出水面前,艇长都必须指挥潜艇在潜望镜深度先用潜望镜对海平面作一次360度的观察,以求尽早发现可能出现的敌情。只有在确认没有任何威胁的情况下潜艇才会浮出水面。
缺陷:潜望镜升至指挥塔外5米高的位置,两端都安装有棱镜和透镜并可将潜望镜的视野放大至1X到6X。潜望镜的使用有两个很明显的问题:当潜望镜完全升起时,细长的潜望镜桅杆会影响潜艇的正常航行,造成横向的不稳定。另外一个重要问题是潜望镜镜片产生的雾气。由于潜艇内部空气潮湿,潜望镜的镜片多会产生雾气,所以潜望镜在设计制造时就必须尽量做到防水和密封。
【点评】激发学生学习的兴趣,体会数学源于生活,服务于生活。
例4:如图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,点D、C分别落在D′、C′的位置上,若∠EFG=55°,求∠1、∠2的度数。
练习:如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿GF折叠成图3,则图3中的∠CFE的度数是 °.
【点评】将折叠与平行线叠加,本质仍然是角平分线与平行线。
例5:如图7-5,已知DE⊥AC,BC⊥AC,FG⊥AB于G,∠1=∠2,则CD⊥AB,为什么?
【思路分析】
解:因为DE⊥AC BC⊥AC 所以DE//BC
所以∠2=∠DCB
又因为∠1=∠2 所以∠1=∠DCB
所以CD//GF
又因为GF⊥AB 所以CD⊥AB
【点评】实际上,在说明GF⊥AB时,也可从同位角或同旁内角的角度,这样,学生更易于接受。
例6 如图7-6,已知∠BED=∠B+∠D,则AB//CD,为什么?
7-6
【思路分析】要得到AB//CD,从已知条件看,只有作EF//AB或EF//CD,借助于已知条件,得出内错角相等,然后才有EF//CD或EF//AB。
法一:解:过E作EF//AB,则∠BED=∠BEF+∠FED
因为EF//AB所以∠BEF=∠B
于是∠BED=∠B+∠FED
又∠BED=∠B+∠D
所以∠FED=∠D所以EF//CD。
而EF//AB 所以AB//CD。
法二:延长BE交CD于点F
因为∠BED=∠B+∠D, ∠BED=∠EFD+∠D
所以∠B=∠EFD
所以AB//CD
【点评】本题主要是“两直线平行,内错角相等”的正、逆向运用。或三角形外角性质与平行线判定
变式题
已知:如图7-7,BE∥DF,∠B=∠D。求证:AD∥BC
【思路分析】 要说明AD∥BC,结合所给的条件:BE∥DF,∠B=∠D,则应从BE∥DF看,由它可得相关和角相等:∠D=∠EAD,再由∠B=∠D可得∠B=∠EAD。
解:因为BE∥DF,所以∠
D=∠EAD,
因为∠B=∠D,所以∠B=∠EAD,所以AD∥BC。
本课小结: 直线平行的条件; 平行线的性质; 平行线、角平分线、等腰三角形的基础题
作业布置
4
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
