2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.4.1二项分布课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高二下学期数学人教A版(2019)选择性必修第三册7.4.1二项分布课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 15:16:18 | ||
图片预览






文档简介
(共21张PPT)
居家学习 悄悄超越
New Semester,new Beginning
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here
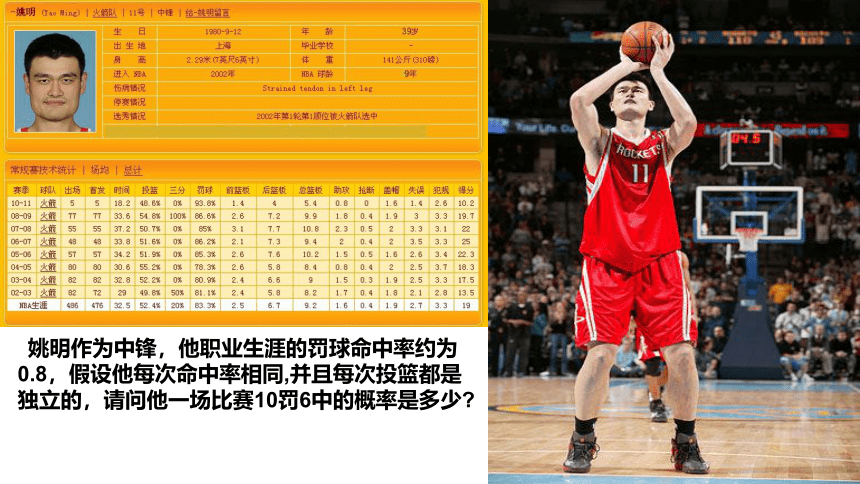
姚明作为中锋,他职业生涯的罚球命中率约为0.8,假设他每次命中率相同,并且每次投篮都是独立的,请问他一场比赛10罚6中的概率是多少
7.4.1二项分布
学习目标
1.理解n重伯努利试验的概念并会判断;
2.理解二项分布的推导过程;
3.理解并能应用二项分布解决实际问题。
4.将实际问题抽象成数学模型,通过观察和揭示解决问题。
★目标达成标志
达成标志1:让学生举出正例与反例;
达成标志2:独立完成由特殊到一般的概括与抽象过程;
达成标志3:应用二项分布解决例1和例2;
达成标志4:探究出例3两种解法的等价性,理解转化过程。
新知探究
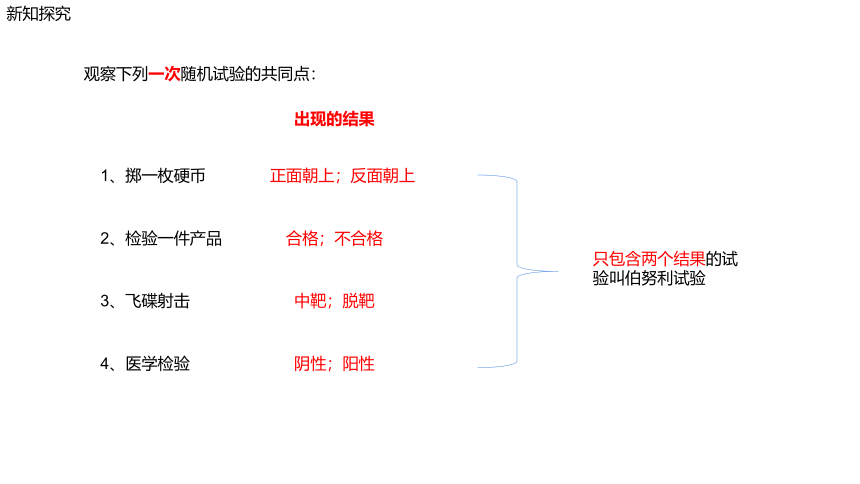
观察下列一次随机试验的共同点:
1、掷一枚硬币
出现的结果
正面朝上;反面朝上
2、检验一件产品
合格;不合格
3、飞碟射击
中靶;脱靶
4、医学检验
阴性;阳性
只包含两个结果的试验叫伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果相互独立.
你知道试验的名字为什么叫“伯努利”吗?
①重复意味着各次试验成功的概率相同。
②旧教材概念:在相同的条件下重复做的n次试验,
称为n次独立重复试验.
练习:判断下列试验是不是n重伯努利试验?
1)、5人投篮,每人各投篮一次。 ( )
2)、袋中有5个白球、3个红球,从中不放回抽出5个球 。( )
3)、袋中有5个白球、3个红球,有放回的依次从中抽出5个球 。 ( )
4)、某人射击,每次击中目标的概率是相同的,他连续射击了十次 。 ( )
5)、投掷一枚图钉三次,每次针尖向上的概率为p 。( )
×
×
√
√
理解概念 模型辨析
√
下面3个随机试验是否为n重伯努利试验 如果是,那么其中的伯努利试验是什么 对于每个试验,定义“成功”的事件为A,那么A的概率是多大 重复试验的次数是多少
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为5%,有放回地随机抽取20件.
思考
伯努利试验:关注某个事件A是否发生,
n重伯努利试验:关注事件A发生的次数X.
进一步地,因为X是一个离散型随机变量,所以我们实际关心的是它的概率分布列.例如,对产品抽样检验,随机抽取n 件,我们关心样本中不合格品数的概率分布列.
探 究
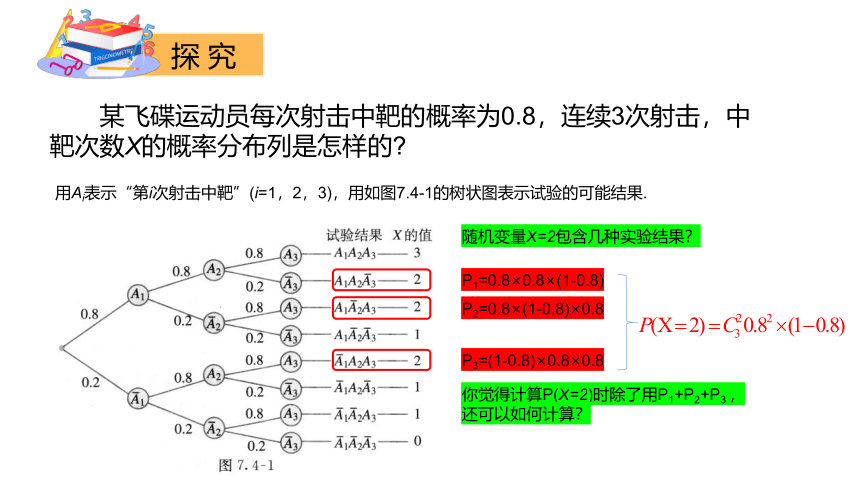
某飞碟运动员每次射击中靶的概率为0.8,连续3次射击,中靶次数X的概率分布列是怎样的
用Ai表示“第i次射击中靶”(i=1,2,3),用如图7.4-1的树状图表示试验的可能结果.
随机变量X=2包含几种实验结果?
P1=0.8×0.8×(1-0.8)
P2=0.8×(1-0.8)×0.8
P3=(1-0.8)×0.8×0.8
你觉得计算P(X=2)时除了用P1+P2+P3 ,
还可以如何计算?
如果连续射击4次,类比上面的分析,表示中靶次数X等于2的结果有哪些 写出中靶次数X的分布列.
思考
归纳
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0如果随机变量X的分布列具有上式的形式,则称随机变量X服从二项分布( binomial distribution),记作X~B(n,p).
(其中k = 0,1,2,···,n )
试验总次数
事件 A 发生的概率
事件 A 发生的次数
[(1-p)+p)]n展开式第k+1项
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1) 恰好出现5次正面朝上的概率;
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
应用
图7.4-2是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木
钉之间留有适当的空隙作为通道,前
面挡有一块玻璃.将小球从顶端放入,
小球下落的过程中,每次碰到小木钉
后都等可能地向左或向右落下,最后
落入底部的格子中.格子从左到右分
别编号为0,1,2,…,10,用X表示
小球最后落入格子的号码,求X的分布
列.
※例2
0
1
2
3
4
5
6
7
8
9
10
应用
应用
甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
例3
“三个臭皮匠,顶个诸葛亮”
练习:设诸葛亮解出某个题目的概率是0.9,三个臭皮匠各自独立解出该题目的概率都是0.6,问诸葛亮和臭皮匠团队哪个解出这一题目的可能性大?(臭皮匠团队成员每人独立解题,且只要有人解出即可)
设事件A:“臭皮匠团队解出该题”
解1:(间接法)
解2:(直接法)
因为0.936>0.9 ,所以臭皮匠胜出的可能性较大
变式:设诸葛亮解出某个题目的概率是0.9,三个臭皮匠各自独立解出该题目的概率都是p ,若臭皮匠团队能解出这一题目的可能性大于诸葛亮,则p至少为多少? (臭皮匠团队成员每人独立解题,且只要有人解出即可)
解:设事件A:“臭皮匠团队解出该题”。
臭皮匠胜出。
思考:二项分布与两点分布有什么关系?
思考:两点分布的均值与方差?
两点分布是特殊的二项分布X~B(1,p)
思考:求出二项分布X~B(3,p)的均值与方差?
猜想:二项分布X~B(n,p)的均值与方差?
练习
n重伯努利试验
二项分布:
n重伯努利试验模型应用
特殊到一般
归纳推理
数学抽象
数学建模
分类讨论
转化与化归
课堂小结、理性升华
线上学习 展翅翱翔
New Semester,new Beginning
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here
居家学习 悄悄超越
New Semester,new Beginning
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here
姚明作为中锋,他职业生涯的罚球命中率约为0.8,假设他每次命中率相同,并且每次投篮都是独立的,请问他一场比赛10罚6中的概率是多少
7.4.1二项分布
学习目标
1.理解n重伯努利试验的概念并会判断;
2.理解二项分布的推导过程;
3.理解并能应用二项分布解决实际问题。
4.将实际问题抽象成数学模型,通过观察和揭示解决问题。
★目标达成标志
达成标志1:让学生举出正例与反例;
达成标志2:独立完成由特殊到一般的概括与抽象过程;
达成标志3:应用二项分布解决例1和例2;
达成标志4:探究出例3两种解法的等价性,理解转化过程。
新知探究
观察下列一次随机试验的共同点:
1、掷一枚硬币
出现的结果
正面朝上;反面朝上
2、检验一件产品
合格;不合格
3、飞碟射击
中靶;脱靶
4、医学检验
阴性;阳性
只包含两个结果的试验叫伯努利试验
我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验.显然,n重伯努利试验具有如下共同特征:
(1)同一个伯努利试验重复做n次;
(2)各次试验的结果相互独立.
你知道试验的名字为什么叫“伯努利”吗?
①重复意味着各次试验成功的概率相同。
②旧教材概念:在相同的条件下重复做的n次试验,
称为n次独立重复试验.
练习:判断下列试验是不是n重伯努利试验?
1)、5人投篮,每人各投篮一次。 ( )
2)、袋中有5个白球、3个红球,从中不放回抽出5个球 。( )
3)、袋中有5个白球、3个红球,有放回的依次从中抽出5个球 。 ( )
4)、某人射击,每次击中目标的概率是相同的,他连续射击了十次 。 ( )
5)、投掷一枚图钉三次,每次针尖向上的概率为p 。( )
×
×
√
√
理解概念 模型辨析
√
下面3个随机试验是否为n重伯努利试验 如果是,那么其中的伯努利试验是什么 对于每个试验,定义“成功”的事件为A,那么A的概率是多大 重复试验的次数是多少
(1)抛掷一枚质地均匀的硬币10次.
(2)某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.
(3)一批产品的次品率为5%,有放回地随机抽取20件.
思考
伯努利试验:关注某个事件A是否发生,
n重伯努利试验:关注事件A发生的次数X.
进一步地,因为X是一个离散型随机变量,所以我们实际关心的是它的概率分布列.例如,对产品抽样检验,随机抽取n 件,我们关心样本中不合格品数的概率分布列.
探 究
某飞碟运动员每次射击中靶的概率为0.8,连续3次射击,中靶次数X的概率分布列是怎样的
用Ai表示“第i次射击中靶”(i=1,2,3),用如图7.4-1的树状图表示试验的可能结果.
随机变量X=2包含几种实验结果?
P1=0.8×0.8×(1-0.8)
P2=0.8×(1-0.8)×0.8
P3=(1-0.8)×0.8×0.8
你觉得计算P(X=2)时除了用P1+P2+P3 ,
还可以如何计算?
如果连续射击4次,类比上面的分析,表示中靶次数X等于2的结果有哪些 写出中靶次数X的分布列.
思考
归纳
一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0
(其中k = 0,1,2,···,n )
试验总次数
事件 A 发生的概率
事件 A 发生的次数
[(1-p)+p)]n展开式第k+1项
例1 将一枚质地均匀的硬币重复抛掷10次,求:
(1) 恰好出现5次正面朝上的概率;
(2)正面朝上出现的频率在[0.4,0.6]内的概率.
应用
图7.4-2是一块高尔顿板的示意图.在一块木板上钉着若干排相互平行但相互错开的圆柱形小木钉,小木
钉之间留有适当的空隙作为通道,前
面挡有一块玻璃.将小球从顶端放入,
小球下落的过程中,每次碰到小木钉
后都等可能地向左或向右落下,最后
落入底部的格子中.格子从左到右分
别编号为0,1,2,…,10,用X表示
小球最后落入格子的号码,求X的分布
列.
※例2
0
1
2
3
4
5
6
7
8
9
10
应用
应用
甲、乙两选手进行象棋比赛,如果每局比赛甲获胜的概率为0.6,乙获胜的概率为0.4,那么采用3局2胜制还是采用5局3胜制对甲更有利
例3
“三个臭皮匠,顶个诸葛亮”
练习:设诸葛亮解出某个题目的概率是0.9,三个臭皮匠各自独立解出该题目的概率都是0.6,问诸葛亮和臭皮匠团队哪个解出这一题目的可能性大?(臭皮匠团队成员每人独立解题,且只要有人解出即可)
设事件A:“臭皮匠团队解出该题”
解1:(间接法)
解2:(直接法)
因为0.936>0.9 ,所以臭皮匠胜出的可能性较大
变式:设诸葛亮解出某个题目的概率是0.9,三个臭皮匠各自独立解出该题目的概率都是p ,若臭皮匠团队能解出这一题目的可能性大于诸葛亮,则p至少为多少? (臭皮匠团队成员每人独立解题,且只要有人解出即可)
解:设事件A:“臭皮匠团队解出该题”。
臭皮匠胜出。
思考:二项分布与两点分布有什么关系?
思考:两点分布的均值与方差?
两点分布是特殊的二项分布X~B(1,p)
思考:求出二项分布X~B(3,p)的均值与方差?
猜想:二项分布X~B(n,p)的均值与方差?
练习
n重伯努利试验
二项分布:
n重伯努利试验模型应用
特殊到一般
归纳推理
数学抽象
数学建模
分类讨论
转化与化归
课堂小结、理性升华
线上学习 展翅翱翔
New Semester,new Beginning
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here
