16．3勾股定理的应用学案

16．3勾股定理的应用
学习目标：能运用勾股定理及直角三角形的判别条件（即勾股定理的逆定理）解决简单的实际问题。
学习重点：利用勾股定理及逆定理，解决实际问题
学习难点：利用数学中的建模思想构造直角三角形，利用勾股定理及逆定理，解决实际问题
学习过程
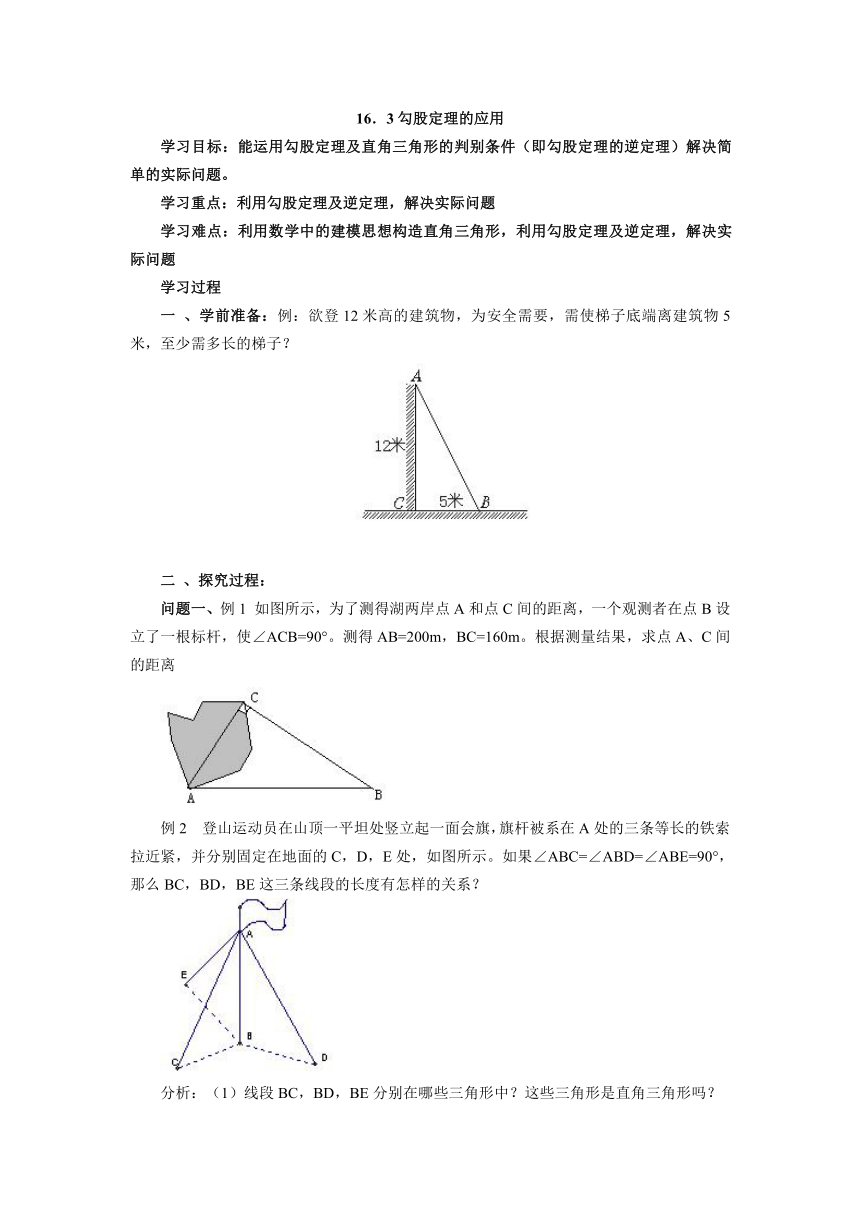
一 、学前准备：例：欲登12米高的建筑物，为安全需要，需使梯子底端离建筑物5米，至少需多长的梯子？
二 、探究过程：
问题一、例1 如图所示，为了测得湖两岸点A和点C间的距离，一个观测者在点B设立了一根标杆，使∠ACB=90°。测得AB=200m，BC=160m。根据测量结果，求点A、C间的距离
例2 登山运动员在山顶一平坦处竖立起一面会旗，旗杆被系在A处的三条等长的铁索拉近紧，并分别固定在地面的C，D，E处，如图所示。如果∠ABC=∠ABD=∠ABE=90°，那么BC，BD，BE这三条线段的长度有怎样的关系？
分析：（1）线段BC，BD，BE分别在哪些三角形中？这些三角形是直角三角形吗？
（2）这些直角三角形的边之间有怎样的关系？
（3）能由已知推出BC，BD，BE长度之间的关系吗？
例3工人在制作铝合金窗框时，为保证窗框的四个角都是直角，有时采用如下的方法：
如图，先亮出框AB，BC的长，再量出两点A，C的距离，由此判断∠B是否直角。
1．判断∠B是否直角的依据是什么？
2．如果AB=1.2m，BC=0.9m，那么，只有当点A，C的距离为多少时，∠B才是直角呢？
三、归纳总结
这节课我们利用勾股定理和它的逆定理解决了生活中的几个实际问题.我们从中可以发现用数学知识解决这些实际问题，更为重要的是将它们转化成数学模型。
四、拓展练习
1、在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇，它高出水面1尺.如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少？
2、“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里，它们离开港口一个半小时后相距30海里．如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
五、课堂检测
1、下列线段不能作为直角三角形三边的是( )
A．3，4，5 B．1，，
C．9，12，15 D．6，2，5
2、等腰三角形底边上的高为12，腰长为13，则它的面积为
3、如图所示，隔湖有两点B，C，从与CB成直角的CA方向上的点A处测得AB=50m，AC=40m，求B，C两点间的距离。

4、如图所示，要修一个种植蔬菜的大棚，棚宽a=6 m，高b=2．5 m，长d=12m．求：覆盖在顶上的塑料薄膜需要的面积。

5、求如图所示(单位:mm)矩形零件上两孔中心A和B的距离(精确到0.1mm).
六、作业：习题 1，2，3