青岛版八年级数学下册6.2平行四边形的判定 导学案(无答案)
文档属性
| 名称 | 青岛版八年级数学下册6.2平行四边形的判定 导学案(无答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 93.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 15:23:53 | ||
图片预览

文档简介
6.2平行四边形的判定 导学案
学习目标:
1.探索判定一个四边形是平行四边形的条件。
2.能从边、角、对角线之间的位置关系和数量关系判定一个四边形是平行四边形。
3.理解并掌握平行四边形的性质和判定之间的互逆关系。
4.能灵活运用平行四边形的特征和判定定理并进行简单的推理证明。
学习重点与难点
重点:平行四边形的判定方法的探索过程。
难点:发展自己的合情推理能力。
学习过程:
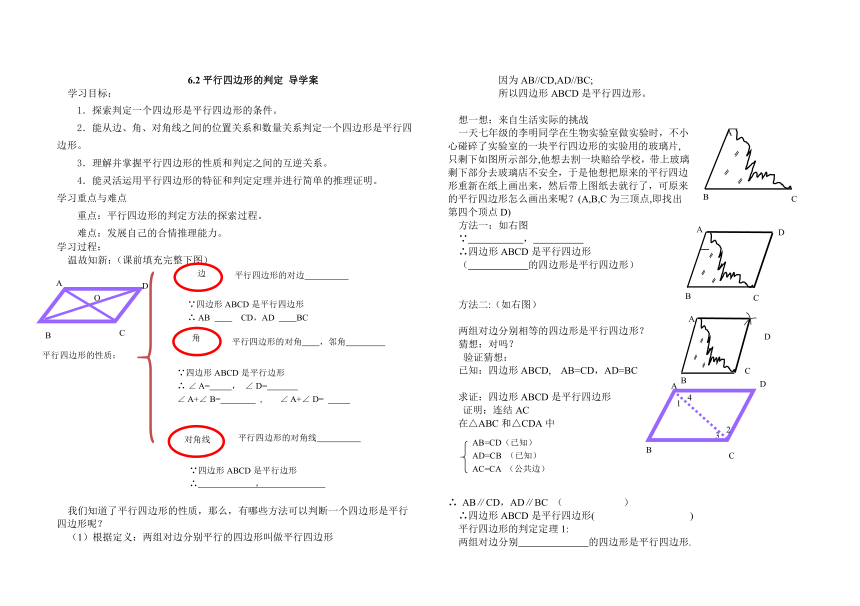
温故知新:(课前填充完整下图)
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
想一想:来自生活实际的挑战
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
方法一:如右图
∵ ,
∴四边形ABCD是平行四边形
( 的四边形是平行四边形)
方法二:(如右图)
两组对边分别相等的四边形是平行四边形?
猜想:对吗?
验证猜想:
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:连结AC
在△ABC和△CDA中
∴ AB∥CD,AD∥BC ( )
∴四边形ABCD是平行四边形( )
平行四边形的判定定理1:
两组对边分别 的四边形是平行四边形.
符号语言:
∵
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
方法三:
对角线互相平分的四边形是平行四边形?
猜想,对吗?
验证猜想:学生自己完成。
平行四边形的判定定理3:
对角线 的四边形是平行四边形。
符号语言:
∵
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
方法四:
两组对角分别相等的四边形是平行四边形?
验证猜想:学生口述过程
结论
平行四边形的判定定理4:
两组对角 的四边形是平行四边形
符号语言由学生自己完成。
方法五:
一组对边平行且相等的四边形是平行四边形?
验证猜想:学生口述过程(尽可能的多种方法证明)
平行四边形的判定定理5:
一组对边 的四边形是平行四边形
符号语言由学生口述完成。
梳理总结,完成下表:
平行四边形的判定方法
综合应用:
1.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
2.请你识别下列四边形哪些是平行四边形 为什么?
3.在下列条件中,不能判定四边形是平行四边形的是( )
A .AB∥CD,AD∥BC B .AB=CD,AD=BC C.AB=CD,AB=CD D.AB∥CD,AD=BC
E.∠A=∠C, ∠B=∠D
4.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
平行四边形的对边
∵四边形ABCD是平行四边形
∴ AB CD,AD BC
EMBED \* MERGEFORMAT
O
B
D
A
C
平行四边形的性质:
对角线
角
边
平行四边形的对角 ,邻角
∵四边形ABCD是平行边形
∴ ∠ A= , ∠ D=
∠ A+∠ B= , ∠ A+∠ D=
平行四边形的对角线
∵四边形ABCD是平行边形
∴ ,
A
B
C
D
A
C
B
B
C
A
D
A
3
D
B
A
C
2
1
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
D
O
A
B
C
⑷
⑶
A
D
C
B
110°
70°
110°
⑴
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
B
C
A
D
D
A
B
C
1、两组对边分别 的四边形是平行四边形
2、两组对边分别 的四边形是平行四边形
从边来判定
3、一组对边 的四边形是平行四边形
从角来判定
4、两组对角分别 的四边形是平行四边形
5、两条对角线 的四边形是平行四边形
从对角线来判定
D
A
B
C
E
F
学习目标:
1.探索判定一个四边形是平行四边形的条件。
2.能从边、角、对角线之间的位置关系和数量关系判定一个四边形是平行四边形。
3.理解并掌握平行四边形的性质和判定之间的互逆关系。
4.能灵活运用平行四边形的特征和判定定理并进行简单的推理证明。
学习重点与难点
重点:平行四边形的判定方法的探索过程。
难点:发展自己的合情推理能力。
学习过程:
温故知新:(课前填充完整下图)
我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。
想一想:来自生活实际的挑战
一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)
方法一:如右图
∵ ,
∴四边形ABCD是平行四边形
( 的四边形是平行四边形)
方法二:(如右图)
两组对边分别相等的四边形是平行四边形?
猜想:对吗?
验证猜想:
已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形
证明:连结AC
在△ABC和△CDA中
∴ AB∥CD,AD∥BC ( )
∴四边形ABCD是平行四边形( )
平行四边形的判定定理1:
两组对边分别 的四边形是平行四边形.
符号语言:
∵
∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)
方法三:
对角线互相平分的四边形是平行四边形?
猜想,对吗?
验证猜想:学生自己完成。
平行四边形的判定定理3:
对角线 的四边形是平行四边形。
符号语言:
∵
∴四边形ABCD是平行四边形
(对角线互相平分的四边形是平行四边形)
方法四:
两组对角分别相等的四边形是平行四边形?
验证猜想:学生口述过程
结论
平行四边形的判定定理4:
两组对角 的四边形是平行四边形
符号语言由学生自己完成。
方法五:
一组对边平行且相等的四边形是平行四边形?
验证猜想:学生口述过程(尽可能的多种方法证明)
平行四边形的判定定理5:
一组对边 的四边形是平行四边形
符号语言由学生口述完成。
梳理总结,完成下表:
平行四边形的判定方法
综合应用:
1.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?
2.请你识别下列四边形哪些是平行四边形 为什么?
3.在下列条件中,不能判定四边形是平行四边形的是( )
A .AB∥CD,AD∥BC B .AB=CD,AD=BC C.AB=CD,AB=CD D.AB∥CD,AD=BC
E.∠A=∠C, ∠B=∠D
4.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
平行四边形的对边
∵四边形ABCD是平行四边形
∴ AB CD,AD BC
EMBED \* MERGEFORMAT
O
B
D
A
C
平行四边形的性质:
对角线
角
边
平行四边形的对角 ,邻角
∵四边形ABCD是平行边形
∴ ∠ A= , ∠ D=
∠ A+∠ B= , ∠ A+∠ D=
平行四边形的对角线
∵四边形ABCD是平行边形
∴ ,
A
B
C
D
A
C
B
B
C
A
D
A
3
D
B
A
C
2
1
4
AB=CD(已知)
AD=CB (已知)
AC=CA (公共边)
D
O
A
B
C
⑷
⑶
A
D
C
B
110°
70°
110°
⑴
A
B
C
D
120°
60°
5㎝
5㎝
A
B
C
D
O
5㎝
5㎝
4㎝
4㎝
B
A
D
C
4.8㎝
4.8㎝
⑵
7.6㎝
7.6㎝
B
C
A
D
D
A
B
C
1、两组对边分别 的四边形是平行四边形
2、两组对边分别 的四边形是平行四边形
从边来判定
3、一组对边 的四边形是平行四边形
从角来判定
4、两组对角分别 的四边形是平行四边形
5、两条对角线 的四边形是平行四边形
从对角线来判定
D
A
B
C
E
F
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
