青岛版八年级数学下册6.3特殊的平行四边形(第三课时) 课件(共30张PPT)
文档属性
| 名称 | 青岛版八年级数学下册6.3特殊的平行四边形(第三课时) 课件(共30张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 15:39:12 | ||
图片预览




文档简介
(共30张PPT)
6.3特殊的平行四边形(3)
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
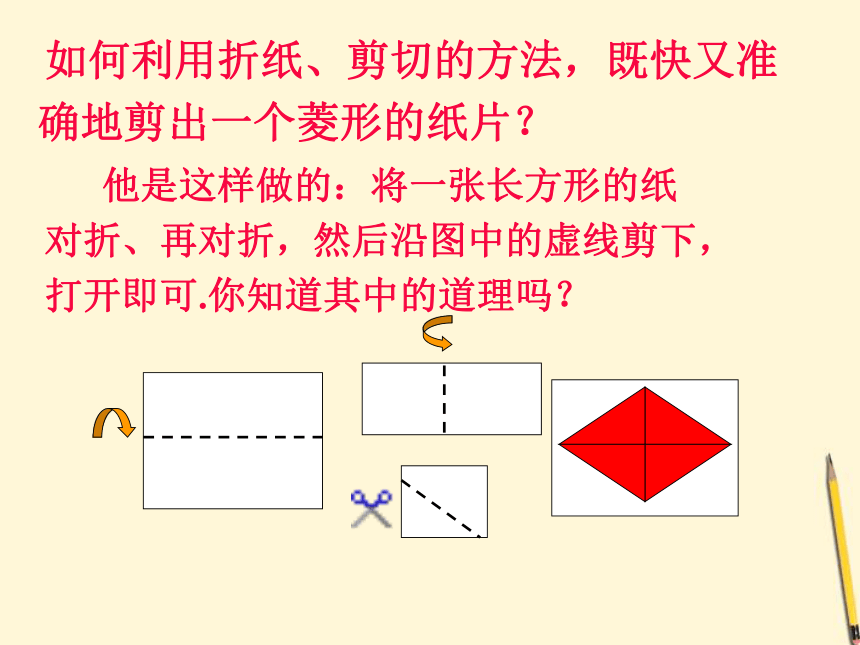
他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质1:菱形的四条边都相等.
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
2、探究性质,尝试证明
∵四边形ABCD是菱形
∴AB=BC=CD=DA
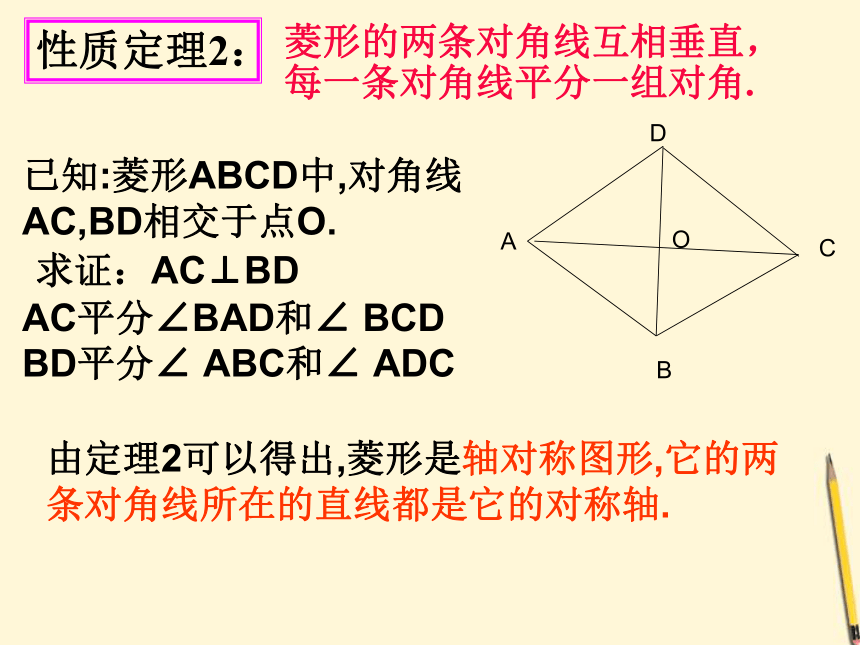
求证:AC⊥BD
已知:菱形ABCD中,对角线AC,BD相交于点O.
AC平分∠BAD和∠ BCD BD平分∠ ABC和∠ ADC
A
B
C
D
O
由定理2可以得出,菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴.
菱形的两条对角线互相垂直,每一条对角线平分一组对角.
性质定理2:
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
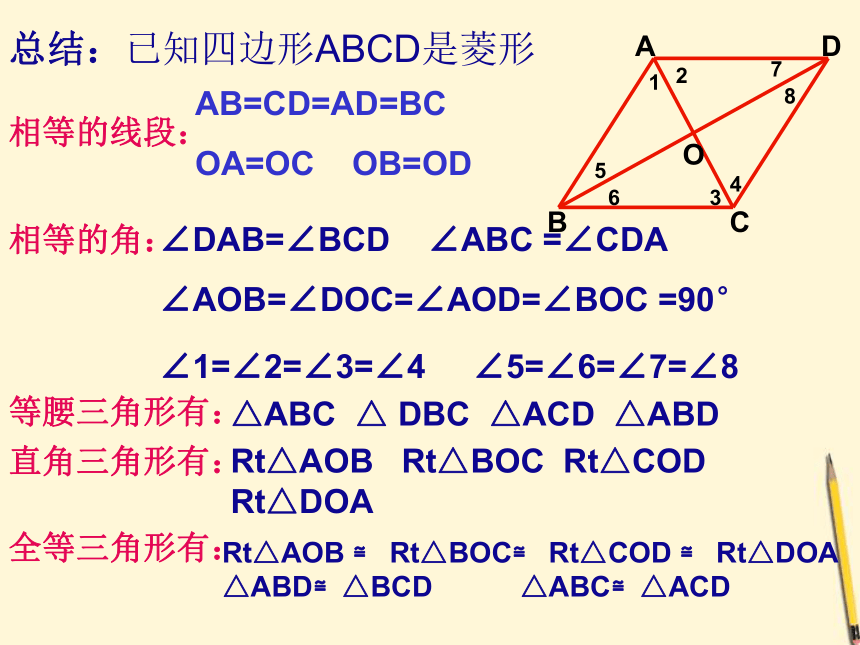
总结:已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
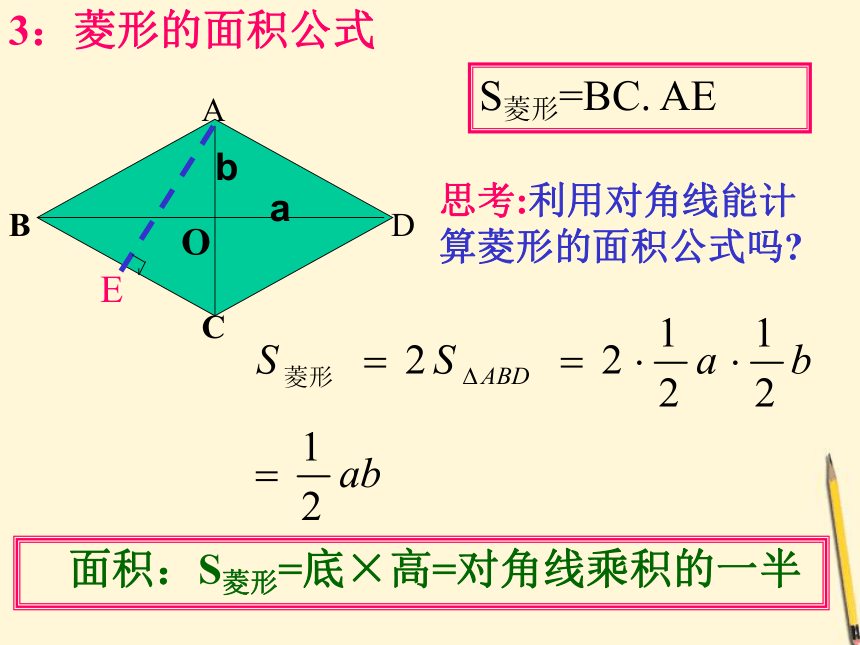
3:菱形的面积公式
A
B
C
D
O
E
S菱形=BC. AE
思考:利用对角线能计算菱形的面积公式吗
面积:S菱形=底×高=对角线乘积的一半
a
b
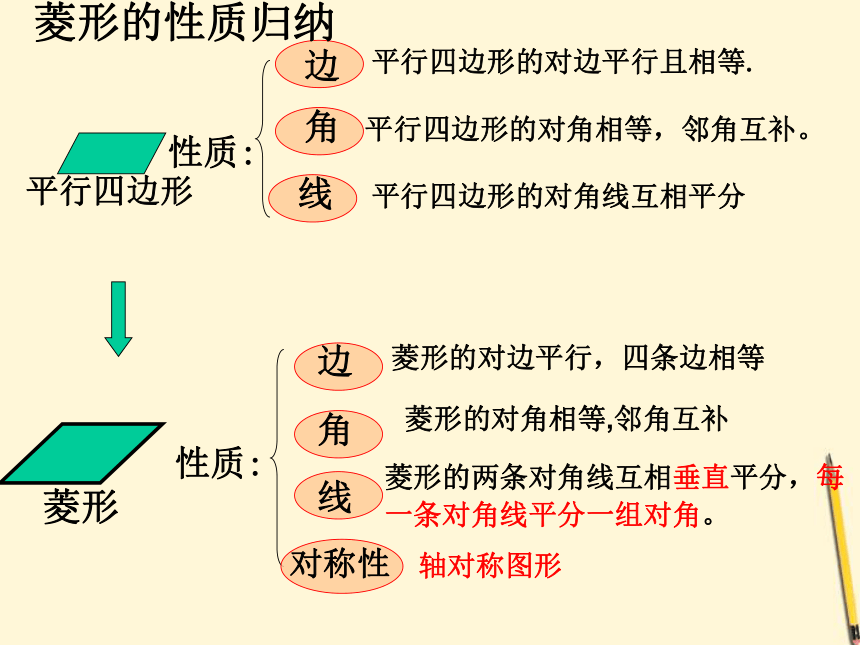
边
角
线
平行四边形的对边平行且相等.
平行四边形的对角相等,邻角互补。
平行四边形的对角线互相平分
边
角
线
对称性
轴对称图形
性质:
菱形
性质:
平行四边形
菱形的对角相等,邻角互补
菱形的对边平行,四条边相等
菱形的两条对角线互相垂直平分,每
一条对角线平分一组对角。
菱形的性质归纳
.
.
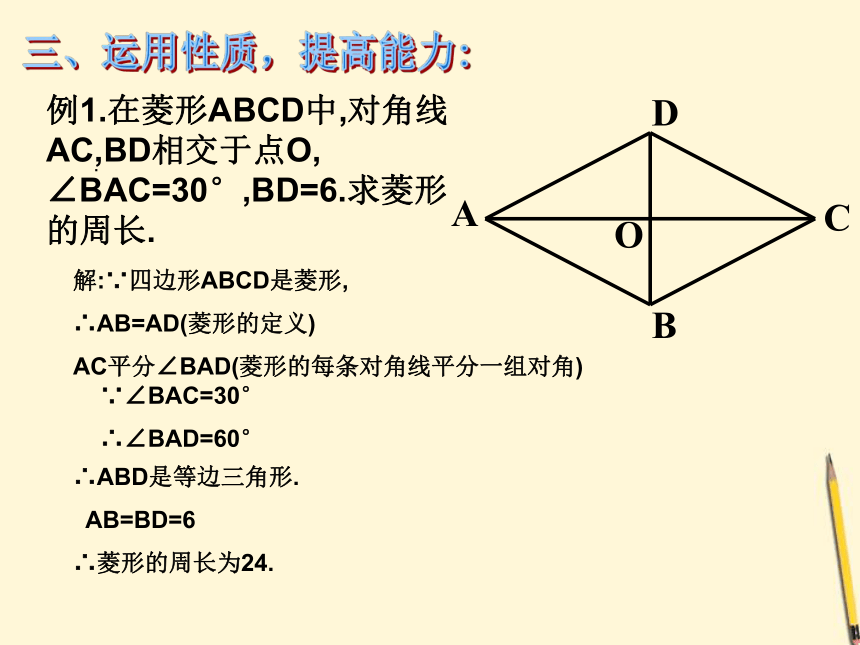
解:∵四边形ABCD是菱形,
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°
∴ABD是等边三角形.
AB=BD=6
∴菱形的周长为24.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的周长.
A
B
C
D
O
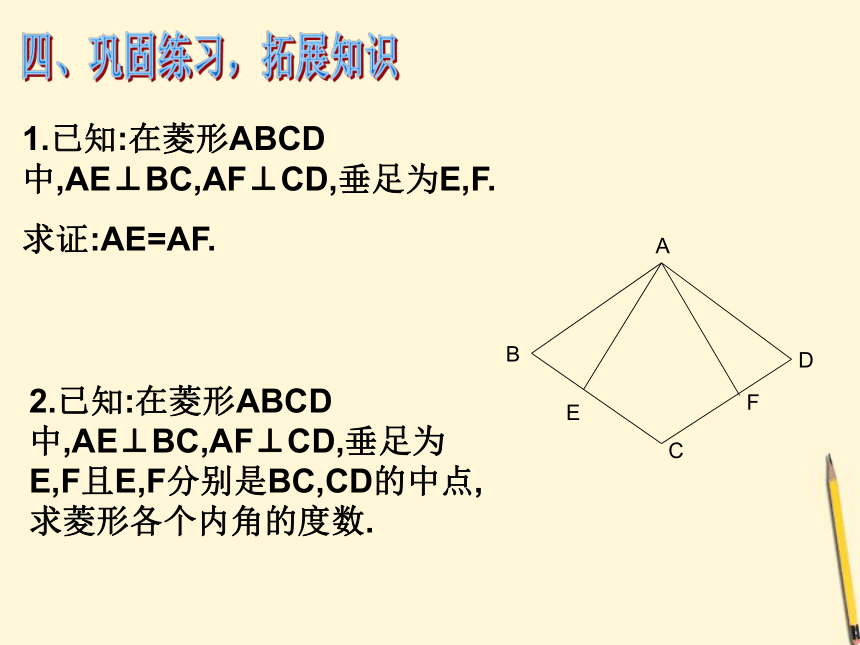
1.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.
求证:AE=AF.
A
B
C
D
E
F
2.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F且E,F分别是BC,CD的中点,求菱形各个内角的度数.
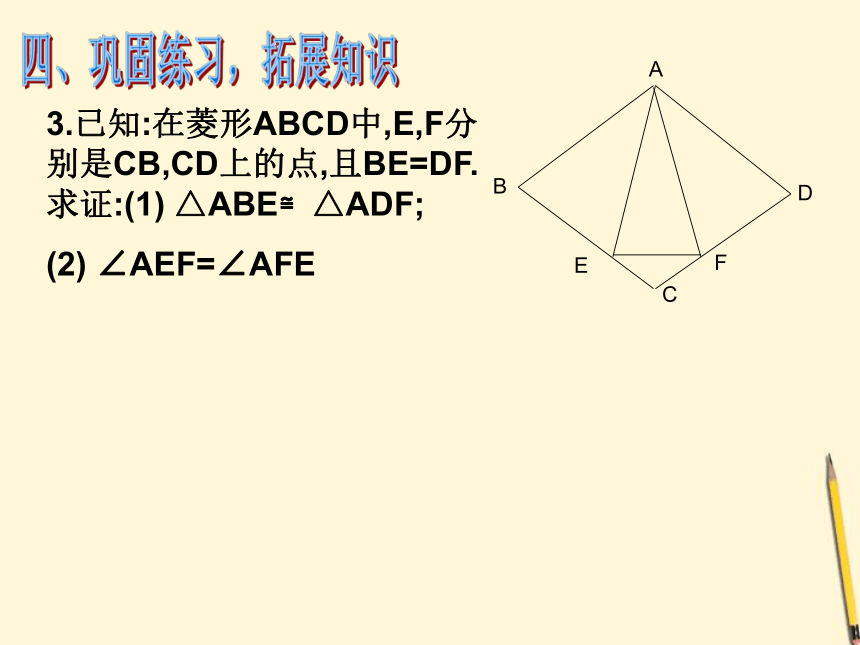
3.已知:在菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.求证:(1) △ABE≌△ADF;
(2) ∠AEF=∠AFE
D
A
B
C
E
F
4.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.
求∠ABC的度数;
A
B
C
D
E
O
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
归纳:1 菱形的定义
2 菱形的性质
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
3、探索判定:想一想
如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
有一组邻边相等的平行四边形叫做菱形.
根据定义得:
A
B
C
D
还有什么方法吗
探究活动
5
5
5
5
5
5
5
5
5
有两条边相等
的四边形是菱形吗?
有三条边相等
有四条边相等
猜想: 有四条边相等的四边形是菱形。
符号语言
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
B
A
D
C
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
∵AD=BC AB=CD
又∵AB=AD
定理: 有四条边相等的四边形是菱形。
画一画
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
你根据什么方法能判定是菱形吗?
有四条边相等的四边形是菱形。
O
∵在四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
D
B
C
思考
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形。
证明:
所以 ABCD是菱形。
因为 AC ⊥ BD,
因为四边形ABCD是平行四边形,
所以OA=OC。
所以BA=BC。
O
定理:对角线互相垂直的平行四边形是菱形.
(线段垂直平分线上的点到线段两个端点的距离相等)
(有一组邻边相等的平行四边形
叫做菱形).
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ □ ABCD是菱形
符号语言
归纳
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
二.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。
(3) PO与CD有怎样的关系?
四边形PCOD是菱形。
PO与CD互相垂直且平分
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
小结:
矩形与菱形
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
有一组邻边相等的平行四边形
对角线互相垂直的平行四边形
四条边都相等的四边形
四条边都相等
检测:
如图,已知AD平分∠BAC,DE//AC,
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)它的周长为多少?
A
B
C
F
D
E
练习:
如图在菱形ABCD中,CE⊥AB,CF⊥AD.
则CE与CF相等吗?说明理由。
BE与DF呢?
A
B
C
D
E
F
6.3特殊的平行四边形(3)
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
菱形
菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.
他是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可.你知道其中的道理吗?
如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?
由于平行四边形的对边相等,而菱形的邻边相等,故:
菱形的性质1:菱形的四条边都相等.
A
B
D
C
菱形是特殊的平行四边形,具有平行四边形的所有性质.
2、探究性质,尝试证明
∵四边形ABCD是菱形
∴AB=BC=CD=DA
求证:AC⊥BD
已知:菱形ABCD中,对角线AC,BD相交于点O.
AC平分∠BAD和∠ BCD BD平分∠ ABC和∠ ADC
A
B
C
D
O
由定理2可以得出,菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴.
菱形的两条对角线互相垂直,每一条对角线平分一组对角.
性质定理2:
相等的线段:
相等的角:
等腰三角形有:
直角三角形有:
全等三角形有:
总结:已知四边形ABCD是菱形
AB=CD=AD=BC
OA=OC OB=OD
∠DAB=∠BCD ∠ABC =∠CDA
∠AOB=∠DOC=∠AOD=∠BOC =90°
∠1=∠2=∠3=∠4 ∠5=∠6=∠7=∠8
△ABC △ DBC △ACD △ABD
Rt△AOB Rt△BOC Rt△COD Rt△DOA
Rt△AOB ≌ Rt△BOC≌ Rt△COD ≌ Rt△DOA
△ABD≌△BCD △ABC≌△ACD
A
B
C
D
O
1
2
3
4
5
6
7
8
3:菱形的面积公式
A
B
C
D
O
E
S菱形=BC. AE
思考:利用对角线能计算菱形的面积公式吗
面积:S菱形=底×高=对角线乘积的一半
a
b
边
角
线
平行四边形的对边平行且相等.
平行四边形的对角相等,邻角互补。
平行四边形的对角线互相平分
边
角
线
对称性
轴对称图形
性质:
菱形
性质:
平行四边形
菱形的对角相等,邻角互补
菱形的对边平行,四条边相等
菱形的两条对角线互相垂直平分,每
一条对角线平分一组对角。
菱形的性质归纳
.
.
解:∵四边形ABCD是菱形,
∴AB=AD(菱形的定义)
AC平分∠BAD(菱形的每条对角线平分一组对角)
∵∠BAC=30°
∴∠BAD=60°
∴ABD是等边三角形.
AB=BD=6
∴菱形的周长为24.
例1.在菱形ABCD中,对角线AC,BD相交于点O, ∠BAC=30°,BD=6.求菱形的周长.
A
B
C
D
O
1.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F.
求证:AE=AF.
A
B
C
D
E
F
2.已知:在菱形ABCD中,AE⊥BC,AF⊥CD,垂足为E,F且E,F分别是BC,CD的中点,求菱形各个内角的度数.
3.已知:在菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.求证:(1) △ABE≌△ADF;
(2) ∠AEF=∠AFE
D
A
B
C
E
F
4.已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=1.
求∠ABC的度数;
A
B
C
D
E
O
一组邻边相等
有一组邻边相等的平行四边形叫做菱形
平行四边形
边
对角线
角
归纳:1 菱形的定义
2 菱形的性质
菱形
菱形的两条对角线互相平分
菱形的两组对边平行
菱形的四条边相等
菱形的两组对角分别相等
菱形的邻角互补
菱形的两条对角线互相垂直,
每一条对角线平分一组对角。
3、探索判定:想一想
如果一个四边形是平行四边形,则只要再有什么条件就可以判定它是一个菱形?根据什么?
有一组邻边相等的平行四边形叫做菱形.
根据定义得:
A
B
C
D
还有什么方法吗
探究活动
5
5
5
5
5
5
5
5
5
有两条边相等
的四边形是菱形吗?
有三条边相等
有四条边相等
猜想: 有四条边相等的四边形是菱形。
符号语言
∴四边形ABCD是平行四边形
已知:在四边形ABCD中,
AB=BC=CD=DA
求证:四边形ABCD是菱形
B
A
D
C
证明:
∴四边形ABCD是菱形
(有一组邻边相等的平行四边形叫做菱形)
∵ AB=BC=CD=DA
∴四边形ABCD是菱形
∵AD=BC AB=CD
又∵AB=AD
定理: 有四条边相等的四边形是菱形。
画一画
先画两条等长的线段AB、AD,然后分别以B、D为圆心,AB为半径画弧,得到两弧的交点C,连接BC、CD,就得到了一个四边形,猜一猜,这是什么四边形?
你根据什么方法能判定是菱形吗?
有四条边相等的四边形是菱形。
O
∵在四边形ABCD中,
AB=BC=CD=DA
∴四边形ABCD是菱形.
A
D
B
C
思考
用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形.转动木条,这个四边形什么时候变成菱形
猜想
对角线互相垂直的平行四边形是菱形.
命题:对角线互相垂直的平行四边形是菱形.
A
B
C
D
已知:在 中,AC ⊥ BD,
ABCD
ABCD
求证: 是菱形。
证明:
所以 ABCD是菱形。
因为 AC ⊥ BD,
因为四边形ABCD是平行四边形,
所以OA=OC。
所以BA=BC。
O
定理:对角线互相垂直的平行四边形是菱形.
(线段垂直平分线上的点到线段两个端点的距离相等)
(有一组邻边相等的平行四边形
叫做菱形).
∵四边形ABCD是平行四边形; AC ⊥ BD;
∴ □ ABCD是菱形
符号语言
归纳
菱形常用的判定方法:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
有四条边相等的四边形是菱形.
判断下列说法是否正确?为什么?
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等
的四边形是菱形;
(4)两条邻边相等,且一条对角线平分一
组对角的四边形是菱形.
√
╳
╳
╳
□ABCD的对角线AC与BD相交于点O, (1)若AB=AD,则□ABCD是 形; (2)若AC=BD,则□ABCD是 形; (3)若∠ABC是直角,则□ABCD是 形; (4)若∠BAO=∠DAO,则□ABCD是 形。
A
B
C
D
O
菱
矩
矩
菱
请你动脑筋
把两张等宽的纸条交叉重叠在一起,你能判断重叠部分ABCD的形状吗?
A
C
D
B
思考:
D
C
B
A
二.已知:如图,矩形ABCD的对角线相交于点O,PD∥AC,PC∥BD,PD、PC相交于点P。
(1)猜想:四边形PCOD是什么特殊的四边形?
(2)试证明你的猜想。
(3) PO与CD有怎样的关系?
四边形PCOD是菱形。
PO与CD互相垂直且平分
一组邻边相等
对角线互相垂直
四条边相等
五种判定方法
四边形
平行四边形
菱形
小结:
矩形与菱形
矩形 菱形
定义
有一角是直角的平行四边形叫做矩形.
有一组邻边相等的平行四边形叫做菱形.
平行四边形的性质
性质
边
角
对角线
四个角都是直角
相等
互相垂直且平分每一组对角
判定
有一角是直角的平行四边形
对角线相等的平行四边形
三个角都是直角的四边形
有一组邻边相等的平行四边形
对角线互相垂直的平行四边形
四条边都相等的四边形
四条边都相等
检测:
如图,已知AD平分∠BAC,DE//AC,
DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)它的周长为多少?
A
B
C
F
D
E
练习:
如图在菱形ABCD中,CE⊥AB,CF⊥AD.
则CE与CF相等吗?说明理由。
BE与DF呢?
A
B
C
D
E
F
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
