北师大版八年级数学下册 6.1 平行四边形的性质(第一课时) 课件 (共14张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 6.1 平行四边形的性质(第一课时) 课件 (共14张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 300.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 15:49:29 | ||
图片预览





文档简介
(共14张PPT)
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
4.1、 平行四边形的性质
(第1课时)
探究活动:
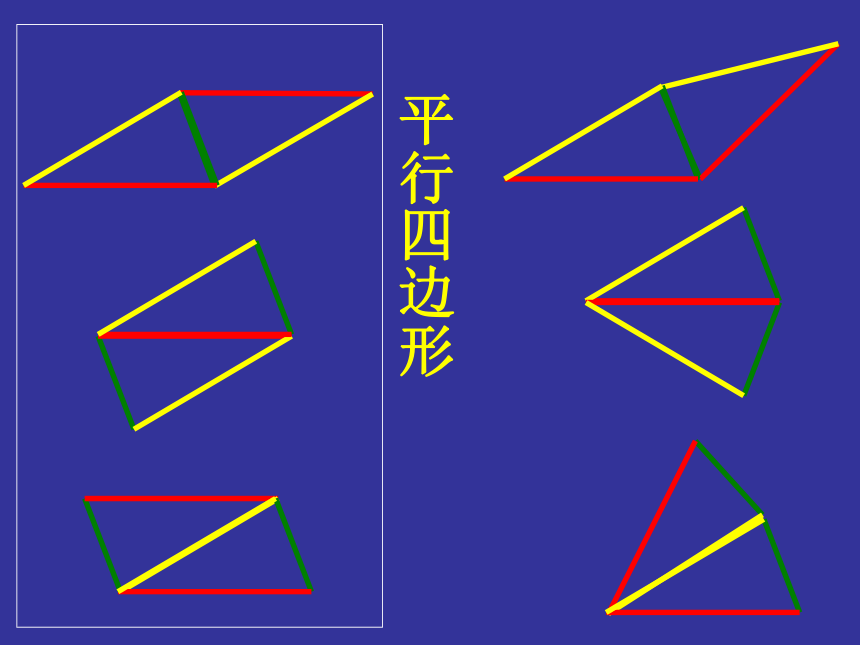
将一张纸对折,剪下两张叠放的三角形纸片,将它们相等的一组边重合,得到一个怎样的四边形?
平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
探究发现1:平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
读作:平行四边形ABCD
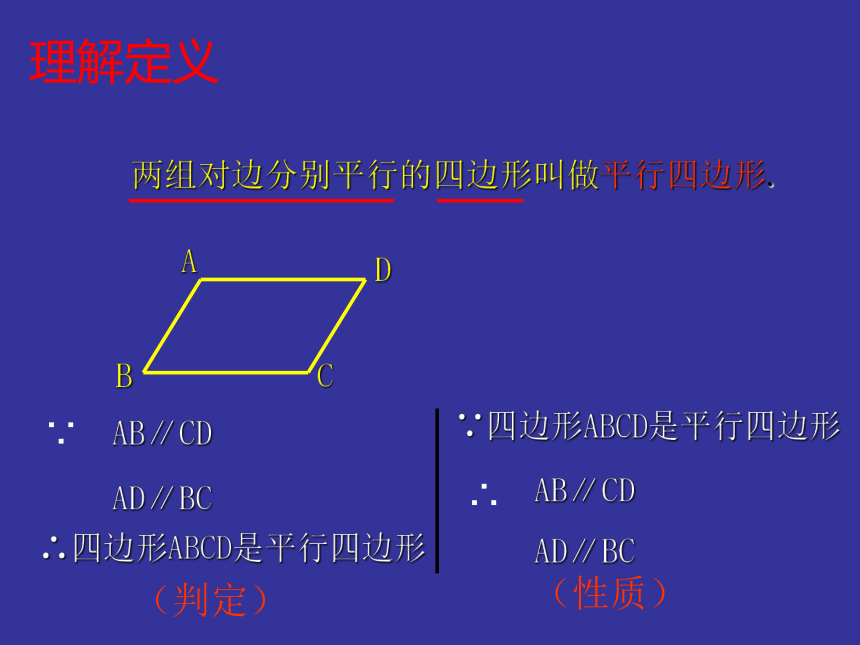
两组对边分别平行的四边形叫做平行四边形.
A
D
B
C
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
(判定)
(性质)
深入探究
做一做
(1)在你拼得得到的平行四边形中,有哪些相等的线段、哪些相等的角?你是如何得到的?与同伴交流。
(2)任意一个平行四边形,是否都可以由两个全等三角形拼接而成?若能,你能对其中一个三角形通过适当的变化而得到另一个三角形吗?从中你又得到哪些结论 与同伴交流。
C
O
B
D
A
o
探究发现2:平行四边形的性质
(A)
(B)
(C)
(D)
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
AB=CD,AD=BC.(平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
D
A
C
B
∴ AB∥CD,AD∥BC (平行四边形的定义)
平行四边形的性质:
定 义:平行四边形的两组对边分别平行
1.如图:在 ABCD中,根据已知你能得到哪些
结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
成果应用:
小结:平行四边形中已知其中一角可求出另外
三个角的度数,已知一组邻边可 求其他边。
考一考
ABCD中, ∠B=600,则∠A= ——, ∠C= ——
∠D=——.
2. ABCD中∠A比∠B大200,则∠C= ————.
3. ABCD中,AB=3cm,BC=5cm,则AD= ——,CD= ——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
(A)5cm ( B )15cm
( C )6cm ( D )16cm
1200
1200
600
1000
5cm
3cm
A
A
D
C
B
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
3、通过本课的探究你认为发现一个数学结论应经历怎样的过程?
课堂小结:
作业
课本习题4.1
1, 2, 3.
探究题 如下图,在 ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q,你能说明MQ=NP吗
师生共勉
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么。
——毕达哥拉斯
4.1、 平行四边形的性质
(第1课时)
探究活动:
将一张纸对折,剪下两张叠放的三角形纸片,将它们相等的一组边重合,得到一个怎样的四边形?
平行四边形
1.两组对边分别平行的四边形叫做平行四边形.
如图:四边形ABCD是平行四边形记作: ABCD
2.平行四边形不相邻的两个顶点连成的线段叫平行四边形的对角线.
3.平行四边形相对的边称为 对边, 相对的角称为 对角.
探究发现1:平行四边形相关概念
A
D
C
B
线段AC、BD就是 ABCD的两条对角线。
对边:AB与CD; BC与DA.
对角: ∠ABC与∠CDA; ∠BAD与∠DCB.
读作:平行四边形ABCD
两组对边分别平行的四边形叫做平行四边形.
A
D
B
C
AB∥CD
AD∥BC
∵
∴四边形ABCD是平行四边形
∵四边形ABCD是平行四边形
AB∥CD
AD∥BC
∴
理解定义
(判定)
(性质)
深入探究
做一做
(1)在你拼得得到的平行四边形中,有哪些相等的线段、哪些相等的角?你是如何得到的?与同伴交流。
(2)任意一个平行四边形,是否都可以由两个全等三角形拼接而成?若能,你能对其中一个三角形通过适当的变化而得到另一个三角形吗?从中你又得到哪些结论 与同伴交流。
C
O
B
D
A
o
探究发现2:平行四边形的性质
(A)
(B)
(C)
(D)
几何语言:
定理1:平行四边形的两组对边分别相等
∵ 四边形ABCD是平行四边形
AB=CD,AD=BC.(平行四边形的对边相等)
∠A= ∠C, ∠B= ∠D(平行四边形的对角相等)
定理2:平行四边形的两组对角分别相等
D
A
C
B
∴ AB∥CD,AD∥BC (平行四边形的定义)
平行四边形的性质:
定 义:平行四边形的两组对边分别平行
1.如图:在 ABCD中,根据已知你能得到哪些
结论?为什么
32cm
30cm
32cm
30cm
A
B
C
D
56°
56°
124°
124°
成果应用:
小结:平行四边形中已知其中一角可求出另外
三个角的度数,已知一组邻边可 求其他边。
考一考
ABCD中, ∠B=600,则∠A= ——, ∠C= ——
∠D=——.
2. ABCD中∠A比∠B大200,则∠C= ————.
3. ABCD中,AB=3cm,BC=5cm,则AD= ——,CD= ——.
4.如果 ABCD的周长为40cm, ABC的周长为25cm,则对角线AC的长是( ).
(A)5cm ( B )15cm
( C )6cm ( D )16cm
1200
1200
600
1000
5cm
3cm
A
A
D
C
B
通过本节课的学习,你有什么收获?
1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
3、通过本课的探究你认为发现一个数学结论应经历怎样的过程?
课堂小结:
作业
课本习题4.1
1, 2, 3.
探究题 如下图,在 ABCD中,平行于对角线AC的直线MN分别交DA,DC的延长线于点M,N,交BA,BC于点P,Q,你能说明MQ=NP吗
师生共勉
把一件平凡的事情做好就是不平凡
把一件简单的事情做好就是不简单
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
