青岛版八年级数学下册 第7章实数复习课件 (共18张PPT)
文档属性
| 名称 | 青岛版八年级数学下册 第7章实数复习课件 (共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 572.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 17:50:11 | ||
图片预览






文档简介
(共18张PPT)
复习目标
1了解无理数与实数的概念,学会区分无理数与有理数,会对实数进行分类
2了解算术平方根,平方根,立方根的概念,会用根号表示数的平方根立方根,掌握三者的区别
3掌握勾股定理及其逆定理的内容。会用勾股定理解决实际问题,会用逆定理判定直角三角形(难点)
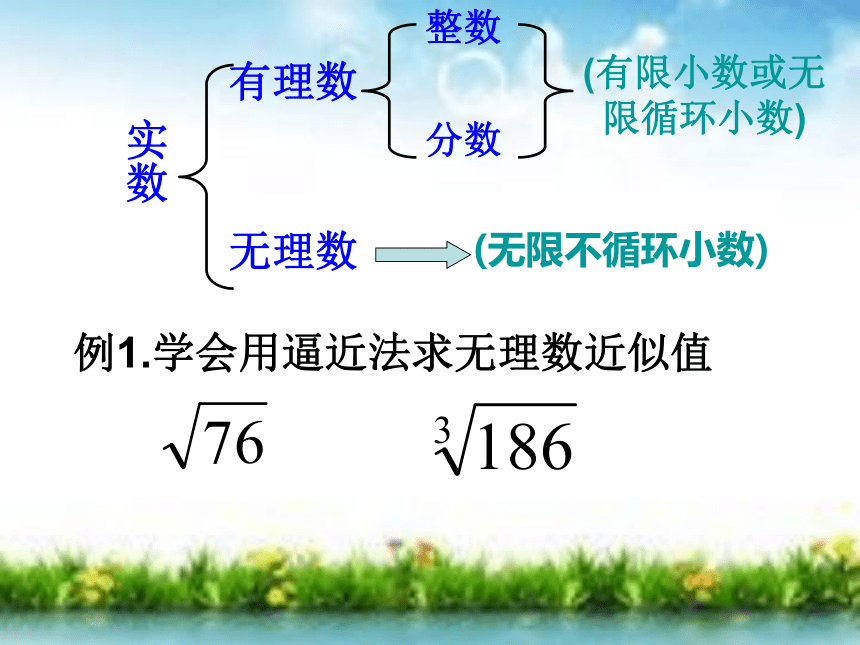
实数
有理数
无理数
整数
分数
(有限小数或无限循环小数)
(无限不循环小数)
例1.学会用逼近法求无理数近似值
例2:把下列各数填入相应的集合里 , , 0.353353335…, , , , 0,
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π
0.353353335…
,0
,π,
在实数范围内,相反数、倒数、绝对值及数的大小比较、运算法则、运算律等仍然适用,和在有理数范围内的意义完全一样。
相反数
⑴相反数:只有符号不同的两个数叫做互为相反数,0的相反数是零。
⑵实数 a 的相反数是-a ;
绝对值
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值是零。
◎下列各组数,互为相反数的( )
A 2和 B(-1) 和1 C -1和(-1) D 2和|-2|
◎ 的倒数是( )
A B - C D –
C
B
【典例】实数 a,b 的位置如图
化简 |a + b| – |a – b|
a
0
b
【解】由数轴可知,a+b<0,a-b<0,从而
原式=-(a+b)-〔-(a-b)〕
= -a-b+(a-b)
= -a-b+(a-b)
= -a-b+a-b
= -2b
小结,做这种类型题目时,先判断绝对值符号里面的数大于0还是小于0
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
是本身
表示方法
的取值
性
质
≥
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
≠
0,1
0
0,1,-1
在立方根中,若被开方数互为相反数,则所求得的立方根也互为相反数
1、若一个数的平方根等于它的立方根,则这个数是
2、如果一个非负数的平方根是2a-1和 a-5,则这个非负数是
3、若 则
(0)
(9)
8或10
4、-27的立方根与 的平方根之和是
(0或-6)
勾股定理 逆定理
两直角边的平方和等于斜边的平方即
若三角形的三边满足
则三角形是直角三角形
是直角三角形的性质
用来判定三角形是否是直角三角形
内容
用途
勾股定理与逆定理
典型题目
张大爷家屋前9米远处有一棵大树。在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米。大树倒下时能砸到张大爷的房子吗?请你通过计算、分析后给出正确的答案
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
3
4
12
13
5
∟
直角三角形两条直角边的长为1和 求斜边上的高
三角形三边 a,b,c满足
则此三角形为
(等腰直角三角形)
1下列说法中①16的平方根是4 ② 9的平方根是 ③-0.0008没有立方根 ④ 27的立方根 是 正确的是
(②)
(D)
2下列能够成直角三角形的是
A 2、4、5 B-3,-4,-5
C 1,2,3 D5,12,13
3、数轴上的点与( )一一对应.
A.整数 B.有理数 C.无理数 D.实数
D
4、相反数是本身的数是 ;绝对值是本身的数 是 ;倒数是本身的数是 .
0
非负数
±1
5、a、b互为相反数,c与d互为倒数, 则a+1+b+cd= .
2
6、 的绝对值为__________.
课堂小结
谈谈这节课有哪些收获
复习目标
1了解无理数与实数的概念,学会区分无理数与有理数,会对实数进行分类
2了解算术平方根,平方根,立方根的概念,会用根号表示数的平方根立方根,掌握三者的区别
3掌握勾股定理及其逆定理的内容。会用勾股定理解决实际问题,会用逆定理判定直角三角形(难点)
实数
有理数
无理数
整数
分数
(有限小数或无限循环小数)
(无限不循环小数)
例1.学会用逼近法求无理数近似值
例2:把下列各数填入相应的集合里 , , 0.353353335…, , , , 0,
整数集合 { …}
分数集合{ … }
无理数集合 { … }
负实数集合{ … }
π
0.353353335…
,0
,π,
在实数范围内,相反数、倒数、绝对值及数的大小比较、运算法则、运算律等仍然适用,和在有理数范围内的意义完全一样。
相反数
⑴相反数:只有符号不同的两个数叫做互为相反数,0的相反数是零。
⑵实数 a 的相反数是-a ;
绝对值
一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,零的绝对值是零。
◎下列各组数,互为相反数的( )
A 2和 B(-1) 和1 C -1和(-1) D 2和|-2|
◎ 的倒数是( )
A B - C D –
C
B
【典例】实数 a,b 的位置如图
化简 |a + b| – |a – b|
a
0
b
【解】由数轴可知,a+b<0,a-b<0,从而
原式=-(a+b)-〔-(a-b)〕
= -a-b+(a-b)
= -a-b+(a-b)
= -a-b+a-b
= -2b
小结,做这种类型题目时,先判断绝对值符号里面的数大于0还是小于0
区别
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
是本身
表示方法
的取值
性
质
≥
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
≠
0,1
0
0,1,-1
在立方根中,若被开方数互为相反数,则所求得的立方根也互为相反数
1、若一个数的平方根等于它的立方根,则这个数是
2、如果一个非负数的平方根是2a-1和 a-5,则这个非负数是
3、若 则
(0)
(9)
8或10
4、-27的立方根与 的平方根之和是
(0或-6)
勾股定理 逆定理
两直角边的平方和等于斜边的平方即
若三角形的三边满足
则三角形是直角三角形
是直角三角形的性质
用来判定三角形是否是直角三角形
内容
用途
勾股定理与逆定理
典型题目
张大爷家屋前9米远处有一棵大树。在一次强风中,这棵大树从离地面6米处折断倒下,量得倒下部分的长是10米。大树倒下时能砸到张大爷的房子吗?请你通过计算、分析后给出正确的答案
已知:如图,四边形ABCD中,∠B=900,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积
A
B
C
D
S四边形ABCD=36
3
4
12
13
5
∟
直角三角形两条直角边的长为1和 求斜边上的高
三角形三边 a,b,c满足
则此三角形为
(等腰直角三角形)
1下列说法中①16的平方根是4 ② 9的平方根是 ③-0.0008没有立方根 ④ 27的立方根 是 正确的是
(②)
(D)
2下列能够成直角三角形的是
A 2、4、5 B-3,-4,-5
C 1,2,3 D5,12,13
3、数轴上的点与( )一一对应.
A.整数 B.有理数 C.无理数 D.实数
D
4、相反数是本身的数是 ;绝对值是本身的数 是 ;倒数是本身的数是 .
0
非负数
±1
5、a、b互为相反数,c与d互为倒数, 则a+1+b+cd= .
2
6、 的绝对值为__________.
课堂小结
谈谈这节课有哪些收获
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
