【高频考点精讲】第8讲-圆的基本定理(PDF版)-人教版数学九年级
文档属性
| 名称 | 【高频考点精讲】第8讲-圆的基本定理(PDF版)-人教版数学九年级 |
|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览




文档简介
第 8 讲 圆的基本定理
【知识结构】
知识模块 具体考法 对应例题
垂径定理求线段 例 1、例 2
垂径定理及其推论
垂径定理的综合 例 3、例 4
弧、弦、圆心角的关系 弧、弦、圆心角的关系 例 5、例 6
圆周角定理 例 7、例 8
圆周角定理 圆内接四边形 例 9
圆周角的综合 例 10、例 11
第 8讲 圆的基本定理
\ 1 /
模块 1 垂径定理及其推论
【知识梳理】
一、垂径定理及其推论
1.圆的对称性:圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
C
如图,CD是 O 的直径,且CD AA';
则 AM A 'M , OAC A 'C , AD A 'D .
A M A'
D
3.垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
4.“知二推三”:
对于一个圆来说,如果具备下列五个条件中的任何两个,那么也具有其他三个:
①垂直于弦;②过圆心;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
【经典例题】
【例1】
1.(互动 1)如图,将半径为 4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为 ( )
A. 4 3cm B. 2 3cm C. 3cm D. 2cm
【解答】解:如图所示,
连接 AO,过O作OD AB ,交 AB 于点 D ,交弦 AB 于点 E ,
AB 折叠后恰好经过圆心,
OE DE ,
O的半径为 4,
1 1
OE OD 4 2,
2 2
第 8讲 圆的基本定理
\ 2 /
OD AB,
1
AE AB,
2
在Rt AOE 中,
AE OA2 OE2 42 22 2 3.
AB 2AE 4 3 .
故选: A .
2.如图,半径为 5 的圆O中, AB 、 DE 是互相垂直的两条弦,垂足为 P ,且 AB ED 8 ,则
OP 3 2 .
【解答】解:作OM AB于 M ,ON DE 于N ,连接OB ,OD,
由垂径定理、勾股定理得:OM ON 52 42 3,
弦 AB 、DE 互相垂直,
DPB 90 ,
OM AB 于 M ,ON DE 于 N ,
OMP ONP 90 ,
四边形MONP是矩形,
OM ON ,
四边形MONP是正方形,
OP 2OM 3 2 ,
故答案为:3 2 .
第 8讲 圆的基本定理
\ 3 /
【例2】
O 中,直径 AB 和弦CD相交于点 E ,已知 AE 1cm,EB 5cm,且 DEB 60 ,求CD的长.
【解答】解:作OP CD于 P ,连接OD,
CP PD,
AE 1, EB 5,
AB 6,
OE 2,
在Rt OPE中,OP 3 ,
PD OD2 OP2 6 ,
CD 2PD 2 6(cm).
【例3】
1.(互动 2) O 的半径为 5cm,弦 AB∥CD ,且 AB 8cm,CD 6cm,则 AB 与CD之间的距离
为 ( )
A.1cm B. 7cm C.3cm或 4cm D.1cm或7cm
【解答】解:①当 AB 、CD在圆心两侧时;
过O作OE CD交CD于 E 点,过O作OF AB交 AB 于F 点,连接OA、OC ,如图 1 所示:
半径 r 5cm,弦 AB / /CD ,且 AB 8cm,CD 6cm,
OA OC 5,CE DE 3cm, AF FB 4cm, E 、 F 、O在一条直线上,
在Rt OEC中,由勾股定理可得:
OE2 OC2 CE2
OE 52 32 4(cm),
在Rt OFA中,由勾股定理可得:
OF 2 OA2 AF 2 ,
OF 52 42 3(cm),
第 8讲 圆的基本定理
\ 4 /
EF OE OF 4 3 7(cm) ,
AB 与CD的距离为 7;
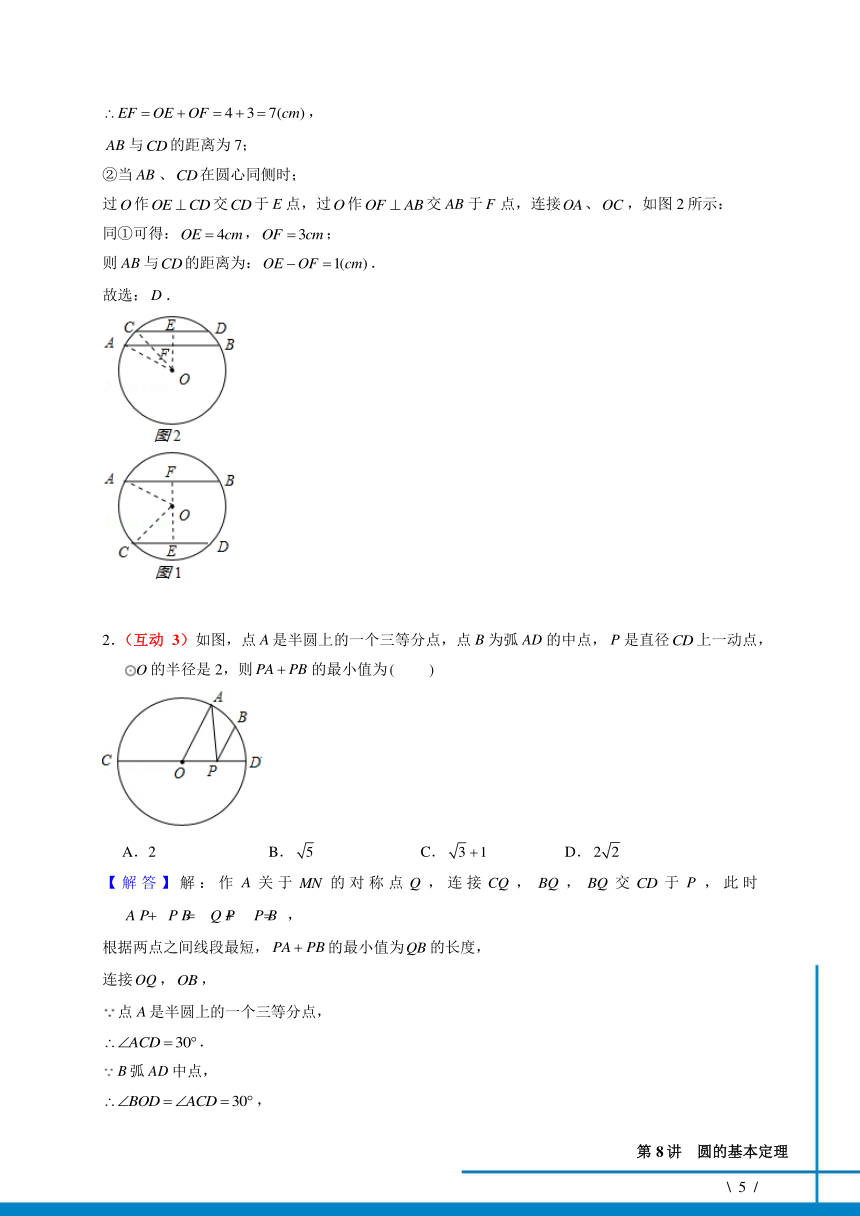
②当 AB 、CD在圆心同侧时;
过O作OE CD交CD于 E 点,过O作OF AB交 AB 于F 点,连接OA、OC ,如图 2 所示:
同①可得:OE 4cm,OF 3cm;
则 AB 与CD的距离为:OE OF 1(cm).
故选:D .
2.(互动 3)如图,点 A 是半圆上的一个三等分点,点 B 为弧 AD 的中点, P 是直径CD上一动点,
O 的半径是 2,则 PA PB 的最小值为 ( )
A.2 B. 5 C. 3 1 D.2 2
【 解 答 】 解 : 作 A 关 于 MN 的 对 称 点 Q , 连 接 CQ , BQ , BQ 交 CD 于 P , 此 时
A P P B Q P P B ,Q B
根据两点之间线段最短, PA PB的最小值为QB 的长度,
连接OQ ,OB ,
点 A 是半圆上的一个三等分点,
ACD 30 .
B弧 AD 中点,
BOD ACD 30 ,
第 8讲 圆的基本定理
\ 5 /
QOD 2 QCD 2 30 60 ,
BOQ 30 60 90 .
O的半径是 2,
OB OQ 2 ,
BQ OB2 OQ2 2 2 ,即 PA PB的最小值为 2 2 .
故选:D .
【例4】
如图,在 O 内有折线OABC ,其中OA 7, AB 12 , A B 60 ,求BC 的长.
【解答】解:
延长 AO交 BC 于 D ,过O作OE BC 于 E ,
OE 过圆心O,OE BC ,
BC 2CE 2BE (垂径定理),
A B 60 ,
DA DB,
DAB 是等边三角形(有一个角等于60 的等腰三角形是等边三角形),
AD BD AB 12, ADB 60 ,
OD AD OA 12 7 5,
OED 90 , ODE 60 ,
DOE 30 ,
1 5
DE OD (在直角三角形中,如果有一个角是30 ,那么它所对的直角边等于斜边的一半),
2 2
第 8讲 圆的基本定理
\ 6 /
5 19
BE 12 , BC 2BE 19(根据垂径定理已推出,在第三行).
2 2
第 8讲 圆的基本定理
\ 7 /
模块 2 弧、弦、圆心角的关系
【知识梳理】
一、弧、弦、圆心角的关系
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2.推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
D
C
O
A B
如图,由定理可知: AOB COD AB CD AB CD
【笔记区】
在同圆或等圆中,弧、弦、圆心角、弦心距可以互相推导
【经典例题】
【例5】
(互动 4)下列说法正确的是 ( )
A.等弧所对的弦相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.相等的圆心角所对的弧相等
【解答】解: A 、正确.本选项符合题意.
B 、错误.应该是平分弦(此弦分直径)的直径垂直弦并平分弦所对的弧,本选项符合题意.
C 、错误,必须在同圆或等圆中,本选项不符合题意.
D 、错误.必须在同圆或等圆中,本选项不符合题意.
故选: A .
第 8讲 圆的基本定理
\ 8 /
【例6】
如图,在△ABC 中, C 90 ,以点 C为圆心,BC 为半径的圆交 AB于点 D,交 AC 于点 E.
(1)若 A 25 ,求 BD的度数;
(2)若BC 9, AC 12 ,求 BD 的长.
【解答】解:(1)连接 CD,如图,
∵ ACB 90 ,
∴ B 90 A 90 25 65 ,
∵CB CD,
∴ CDB B 65 ,
∴ BCD 180 2 B 50 ,
∴ BD的度数为50 ;
(2)作 CH⊥BD,如图,则 BH DH ,
在 Rt△ACB 中, AB 92 122 15 ,
1 1
∵ CH AB BC AC ,
2 2
9 12 36
∴CH ,
15 5
2
2 36 27在 Rt△BCH 中, BH 9 ,
5 5
54
∴ BD 2BH .
5
第 8讲 圆的基本定理
\ 9 /
模块 3 圆周角定理
【知识梳理】
一、圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
C
O
A
B
AOB 2 ACB
二、圆周角定理的推论
1.推论 1:同弧或等弧所对的圆周角相等.
E C
O
D B
A
若 AB AD,则 ACB AED .
2.推论 2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
C
A B
O
若 AB 是 O 的直径,则 ACB是直角.
三、圆内接多边形
1.圆内接多边形:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这
个圆叫做多边形的外接圆.
2.圆内接四边形的性质:
第 8讲 圆的基本定理
\ 10 /
(1)性质 1:圆内接四边形的对角互补.
(2)性质 2:圆内接四边形的任意一个外角等于它的内对角.
D
A
O
E
C
B
如图,点 A、B、C、D 都在圆上,则 A BCD 180 , B D 180 , DCE A .
【经典例题】
【例7】
1.如图,在 O 中, AB AC,若 ABC 57.5 ,则弦 BC 所对的圆周角的度数为____________.
【解答】解: AB AC , ABC 57.5 ,
ACB ABC 57.5 ,
A 180 ABC ACB 65 ,
65 或115
2.(互动 5)如图, M 过点O(0,0) , A( 3 , 0) ,B(0,1),点C 是 x 轴上方弧 AB 上的一点,连
接 BC ,CO,则 BCO的度数是 ( )
A.15 B.30 C. 45 D.60
【解答】解:连接 AB ,如图,
A( 3 , 0) , B(0,1),
第 8讲 圆的基本定理
\ 11 /
OA 3 ,OB 1,
OB 1 3
tan BAO ,
OA 3 3
BAO 30 ,
BCO 30 .
故选: B .
【例8】
1.(互动 6)如图,在 ABC 中, AB AC.以 AB 为直径作半圆O,交 BC 于点 D ,交 AC 于点
E ,若 C 70 ,则 ABE 的度数是 ( )
A.50 B. 65 C. 70 D.80
【解答】解: AB AC , C 70 ,
BAC 40 ,
AB 是直径,
BAE ABE 90 ,
ABE 90 BAE 90 40 50 ,
故选: A .
第 8讲 圆的基本定理
\ 12 /
2.(互动 7)如图,矩形 ABCD 中, AB 3 , BC 8 ,点 P 为矩形内一动点,且满足
PBC PCD,则线段 PD的最小值为 ( )
A.5 B.1 C.2 D.3
【解答】解: 四边形 ABCD为矩形,
BCD 90 ,
PBC PCD,
PBC PCB 90 ,
BPC 90 ,
点 P 在以BC为直径的 O 上,
连接OD交 O 于 P ,连接OP 、 PD,如图,
PD OD OP(当且仅当O、 P 、 D 共线时,取等号),
即 P 点运动到 P 位置时, PD的值最小,最小值为DP ,
1
在Rt OCD中,OC BC 4,CD AB 3,
2
OD 32 42 5,
DP OD OP 5 4 1,
线段 PD的最小值为 1.
故选: B .
【例9】
如图,两圆 O 和 O 相交于 A 、 B1 2 两点, DBC 和 EAO1都是直线,且 AO1C 140 ,那么 E
110 度.
第 8讲 圆的基本定理
\ 13 /
【解答】解:连接 AB , E 110 .
【例10】
如图,在 O 中,直径 AB 10 ,弦 AC 6, ACB 的平分线交 O 于点D .
求 BC , AD , BD的长.
【解答】解: AB 是直径
ACB ADB 90
在Rt ABC中, AB2 AC2 BC2 , AB 10cm, AC 6cm
BC2 AB2 AC2 102 62 64
BC 64 8(cm)
又 CD平分 ACB,
AD BD ,
AD BD,
又 在 2 2 2Rt ABD中, AD BD AB
AD2 BD2 102
100
AD BD 5 2(cm).
2
第 8讲 圆的基本定理
\ 14 /
【例11】
研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图 1,已知
四边形 ABCD内接于 O ,对角线 AC BD,且 AC BD.
(1)求证: AB CD;
(2)若 O 的半径为 8,弧 BD的度数为120 ,求四边形 ABCD的面积;
(3)如图 2,作OM BC 于 M ,请猜测OM 与 AD 的数量关系,并证明你的结论.
【解答】(1)证明: AC BD,
AC BD ,
则 AB DC ,
AB CD;
(2)解:连接OB 、OD,作OH BD于H ,
弧 BD的度数为120 ,
BOD 120 ,
BOH 60 ,
3
则 BH OB 4 3 ,
2
BD 8 3 ,
1
则四边形 ABCD的面积 AC BD 96;
2
(3) AD 2OM ,
连结OB 、OC 、OA、OD,作OE AD于 E ,如图 2,
OE AD,
第 8讲 圆的基本定理
\ 15 /
AE DE ,
BOC 2 BAC ,
而 BOC 2 BOM ,
BOM BAC,
同理可得 AOE ABD,
BD AC,
BAC ABD 90 ,
BOM AOE 90 ,
BOM OBM 90 ,
OBM AOE ,
在 BOM 和 OAE中,
OMB OEA
OBM OAE ,
OB OA
BOM OAE ,
OM AE ,
AD 2OM .
备选题
【备1】
如图, O 与矩形 ABCD 的边 AB 、 CD 分别相交于点 E 、 F 、 G 、 H ,若 AE CH 6 ,则
BG DF为 6 .
【解答】解:作OM GH 于 M ,OM 交 EF 于 N ,如图,
EF / /GH ,
第 8讲 圆的基本定理
\ 16 /
OM EF ,
EN FN ,GM HM ,
易得四边形 ABMN 和四边形MNDC 为矩形,
AN BM , DN CM ,
BG DF BM GM DN NF
AN HM CM EN
AN EN CM HM
AE CH
6.
故答案为 6.
【备2】
如图,在 O 中,弦 AB 8,点C 在 AB 上移动,连接OC ,过点C 作CD OC 交 O 于点 D ,则
CD的最大值是 ( )
A.2 B.4 C.6 D.8
【解答】解:作OH AB于 H ,连接OA、OD,如图,
1 1
AH BH AB 8 4,
2 2
CD OC ,
CD OD2 OC2 ,
而OD为定值,OC 最小时,CD最大,
当OC OH 时,CD的值最大,
CD的最大值为 4.
故选: B .
第 8讲 圆的基本定理
\ 17 /
第 8讲 圆的基本定理
\ 18 /
挑战极限
如图, AB 是 O 的直径,C、D 为圆上两点,且 OAC 30 ,OD 绕着点O 顺时针旋转,连结
CD交直线 AB 于点 E ,当DE OD时, OCE的大小可能为_________________.
【原题】如图, AB 是 O 的直径,点C , D 在 O 上,且 OAC 30 ,OD绕着点O顺时针旋转,
连结CD交直线 AB 于点 E ,当 DE OD时, OCE的大小可能为 ( )
A. 20 B. 70 C.80 D.20 、 40 或80
【解答】解:
连接OC ,
①如图 1,OD绕着点O顺时针旋转,连结CD交直线 AB 于点 E ,
设 OCE x,
OC OD,
OCE D x,
OA OC,
OCA A 30 ,
DE OD,
DOE DEO 30 x 30 60 x
第 8讲 圆的基本定理
\ 19 /
2(60 x) x 180
解得 x 20 .
OCE 的大小为20 ;
②如图 2,
设 OEC x,
DE OD,
EOD E x,
DO CO,
ODC OCD 2x,
EOC 2 A 60
在 OCE 中,
x 60 2x 180 ,
解得 x 40 ,
OCE 2x 80 ;
③如图 3,
设 ACE x,
OA OC,
OCA OAC 30 ,
OC OD,
OCD ODC 30 x,
OD DE
第 8讲 圆的基本定理
\ 20 /
1 1
E ODC 15 x ,
2 2
1
15 x x 30
2
解得 x 10 ,
OCE 30 x 40 .
综上: OCE的大小为:20 、 40 、80 .
故选:D.
第 8讲 圆的基本定理
\ 21 /
巩固练习
【练习1】
1.如图, ABC 内接于 O ,若 A 45 ,OC 2,则 BC 的长为 ( )
A. 2 B. 2 2 C. 2 3 D.4
【解答】解:由圆周角定理得, BOC 2 A 90 ,
BC 2OC 2 2 ,
故选: B .
2.如图,已知 A 、 B 、C 、 D 、 E 均在 O 上,且 AC 为 O 的直径,则 A B C 的度数为
( )
A. 45 B. 60 C.90 D.120
【解答】解: AC 为 O 的直径,
AE ED CD的度数是180 ,
A B C 90 ,
故选:C .
【练习2】
如图,一把直角三角板的顶点 A 、 B 在 O 上,边 BC 、 AC 与 O 交于点 D 、 E ,已知 C 30 ,
AED的大小为 ( )
A.90 B.100 C.110 D.120
第 8讲 圆的基本定理
\ 22 /
【解答】解: A 90 , C 30 ,
B 90 30 60 ,
四边形 ABDE 是圆内接四边形,
AED 180 B 120 ,
故选:D .
【练习3】
如图,已知 AB 是 O 的直径,弦 CD 交 AB 于点 E , CEA 30 , OF CD ,垂足为点 F ,
DE 5,OF 1,那么CD 10 2 3 .
【解答】解: AB 是 O 的直径,OF CD,
根据垂径定理可知:
CF DF ,
CEA 30 ,
OEF 30 ,
OE 2, EF 3 ,
DF DE EF 5 3 ,
CD 2DF 10 2 3 .
故答案为:10 2 3 .
【练习4】
如图, O 的弦 AB 、DC的延长线相交于点 E .
(1)如图 1,若 AD 为120 , BC 为50 ,求 E 的度数;
(2)如图 2,若 AB CD,求证: AE DE .
第 8讲 圆的基本定理
\ 23 /
【解答】(1)解:连接 AC .
弧 AD 为120 ,弧 BC 为50 ,
ACD 60 , BAC 25 ,
ACD BAC E
E ACD BAC 60 25 35 ;
(2)证明:连接 AD .
AB CD,
弧 AB 弧CD,
弧 AC 弧 BD,
ADC DAB ,
AE DE .
【练习5】
如图, MB, MD 是 O 的两条弦,点 A ,C 分别在MB,MD 上,且 AB CD,M 是 AC 的中点.
(1)求证:MB MD ;
(2)过O作OE MB于点 E ,当OE 1,MD 4时,求 O 的半径.
【解答】(1)证明: AB CD,
AB CD ,
M 是 AC 的中点,
第 8讲 圆的基本定理
\ 24 /
AM CM ,
BM DM ,
BM DM .
(2)解:如图,连接OM .
DM BM 4,OE BM ,
EM BE 2 ,
OE 1, OEM 90 ,
OM OE2 EM 2 12 22 5 ,
O的半径为 5 .
第 8讲 圆的基本定理
\ 25 /
【知识结构】
知识模块 具体考法 对应例题
垂径定理求线段 例 1、例 2
垂径定理及其推论
垂径定理的综合 例 3、例 4
弧、弦、圆心角的关系 弧、弦、圆心角的关系 例 5、例 6
圆周角定理 例 7、例 8
圆周角定理 圆内接四边形 例 9
圆周角的综合 例 10、例 11
第 8讲 圆的基本定理
\ 1 /
模块 1 垂径定理及其推论
【知识梳理】
一、垂径定理及其推论
1.圆的对称性:圆是轴对称图形,任何一条直径所在直线都是圆的对称轴.
2.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
C
如图,CD是 O 的直径,且CD AA';
则 AM A 'M , OAC A 'C , AD A 'D .
A M A'
D
3.垂径定理推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
4.“知二推三”:
对于一个圆来说,如果具备下列五个条件中的任何两个,那么也具有其他三个:
①垂直于弦;②过圆心;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧.
【经典例题】
【例1】
1.(互动 1)如图,将半径为 4cm的圆折叠后,圆弧恰好经过圆心,则折痕的长为 ( )
A. 4 3cm B. 2 3cm C. 3cm D. 2cm
【解答】解:如图所示,
连接 AO,过O作OD AB ,交 AB 于点 D ,交弦 AB 于点 E ,
AB 折叠后恰好经过圆心,
OE DE ,
O的半径为 4,
1 1
OE OD 4 2,
2 2
第 8讲 圆的基本定理
\ 2 /
OD AB,
1
AE AB,
2
在Rt AOE 中,
AE OA2 OE2 42 22 2 3.
AB 2AE 4 3 .
故选: A .
2.如图,半径为 5 的圆O中, AB 、 DE 是互相垂直的两条弦,垂足为 P ,且 AB ED 8 ,则
OP 3 2 .
【解答】解:作OM AB于 M ,ON DE 于N ,连接OB ,OD,
由垂径定理、勾股定理得:OM ON 52 42 3,
弦 AB 、DE 互相垂直,
DPB 90 ,
OM AB 于 M ,ON DE 于 N ,
OMP ONP 90 ,
四边形MONP是矩形,
OM ON ,
四边形MONP是正方形,
OP 2OM 3 2 ,
故答案为:3 2 .
第 8讲 圆的基本定理
\ 3 /
【例2】
O 中,直径 AB 和弦CD相交于点 E ,已知 AE 1cm,EB 5cm,且 DEB 60 ,求CD的长.
【解答】解:作OP CD于 P ,连接OD,
CP PD,
AE 1, EB 5,
AB 6,
OE 2,
在Rt OPE中,OP 3 ,
PD OD2 OP2 6 ,
CD 2PD 2 6(cm).
【例3】
1.(互动 2) O 的半径为 5cm,弦 AB∥CD ,且 AB 8cm,CD 6cm,则 AB 与CD之间的距离
为 ( )
A.1cm B. 7cm C.3cm或 4cm D.1cm或7cm
【解答】解:①当 AB 、CD在圆心两侧时;
过O作OE CD交CD于 E 点,过O作OF AB交 AB 于F 点,连接OA、OC ,如图 1 所示:
半径 r 5cm,弦 AB / /CD ,且 AB 8cm,CD 6cm,
OA OC 5,CE DE 3cm, AF FB 4cm, E 、 F 、O在一条直线上,
在Rt OEC中,由勾股定理可得:
OE2 OC2 CE2
OE 52 32 4(cm),
在Rt OFA中,由勾股定理可得:
OF 2 OA2 AF 2 ,
OF 52 42 3(cm),
第 8讲 圆的基本定理
\ 4 /
EF OE OF 4 3 7(cm) ,
AB 与CD的距离为 7;
②当 AB 、CD在圆心同侧时;
过O作OE CD交CD于 E 点,过O作OF AB交 AB 于F 点,连接OA、OC ,如图 2 所示:
同①可得:OE 4cm,OF 3cm;
则 AB 与CD的距离为:OE OF 1(cm).
故选:D .
2.(互动 3)如图,点 A 是半圆上的一个三等分点,点 B 为弧 AD 的中点, P 是直径CD上一动点,
O 的半径是 2,则 PA PB 的最小值为 ( )
A.2 B. 5 C. 3 1 D.2 2
【 解 答 】 解 : 作 A 关 于 MN 的 对 称 点 Q , 连 接 CQ , BQ , BQ 交 CD 于 P , 此 时
A P P B Q P P B ,Q B
根据两点之间线段最短, PA PB的最小值为QB 的长度,
连接OQ ,OB ,
点 A 是半圆上的一个三等分点,
ACD 30 .
B弧 AD 中点,
BOD ACD 30 ,
第 8讲 圆的基本定理
\ 5 /
QOD 2 QCD 2 30 60 ,
BOQ 30 60 90 .
O的半径是 2,
OB OQ 2 ,
BQ OB2 OQ2 2 2 ,即 PA PB的最小值为 2 2 .
故选:D .
【例4】
如图,在 O 内有折线OABC ,其中OA 7, AB 12 , A B 60 ,求BC 的长.
【解答】解:
延长 AO交 BC 于 D ,过O作OE BC 于 E ,
OE 过圆心O,OE BC ,
BC 2CE 2BE (垂径定理),
A B 60 ,
DA DB,
DAB 是等边三角形(有一个角等于60 的等腰三角形是等边三角形),
AD BD AB 12, ADB 60 ,
OD AD OA 12 7 5,
OED 90 , ODE 60 ,
DOE 30 ,
1 5
DE OD (在直角三角形中,如果有一个角是30 ,那么它所对的直角边等于斜边的一半),
2 2
第 8讲 圆的基本定理
\ 6 /
5 19
BE 12 , BC 2BE 19(根据垂径定理已推出,在第三行).
2 2
第 8讲 圆的基本定理
\ 7 /
模块 2 弧、弦、圆心角的关系
【知识梳理】
一、弧、弦、圆心角的关系
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
2.推论:在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
D
C
O
A B
如图,由定理可知: AOB COD AB CD AB CD
【笔记区】
在同圆或等圆中,弧、弦、圆心角、弦心距可以互相推导
【经典例题】
【例5】
(互动 4)下列说法正确的是 ( )
A.等弧所对的弦相等
B.平分弦的直径垂直弦并平分弦所对的弧
C.相等的弦所对的圆心角相等
D.相等的圆心角所对的弧相等
【解答】解: A 、正确.本选项符合题意.
B 、错误.应该是平分弦(此弦分直径)的直径垂直弦并平分弦所对的弧,本选项符合题意.
C 、错误,必须在同圆或等圆中,本选项不符合题意.
D 、错误.必须在同圆或等圆中,本选项不符合题意.
故选: A .
第 8讲 圆的基本定理
\ 8 /
【例6】
如图,在△ABC 中, C 90 ,以点 C为圆心,BC 为半径的圆交 AB于点 D,交 AC 于点 E.
(1)若 A 25 ,求 BD的度数;
(2)若BC 9, AC 12 ,求 BD 的长.
【解答】解:(1)连接 CD,如图,
∵ ACB 90 ,
∴ B 90 A 90 25 65 ,
∵CB CD,
∴ CDB B 65 ,
∴ BCD 180 2 B 50 ,
∴ BD的度数为50 ;
(2)作 CH⊥BD,如图,则 BH DH ,
在 Rt△ACB 中, AB 92 122 15 ,
1 1
∵ CH AB BC AC ,
2 2
9 12 36
∴CH ,
15 5
2
2 36 27在 Rt△BCH 中, BH 9 ,
5 5
54
∴ BD 2BH .
5
第 8讲 圆的基本定理
\ 9 /
模块 3 圆周角定理
【知识梳理】
一、圆周角定理
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
C
O
A
B
AOB 2 ACB
二、圆周角定理的推论
1.推论 1:同弧或等弧所对的圆周角相等.
E C
O
D B
A
若 AB AD,则 ACB AED .
2.推论 2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
C
A B
O
若 AB 是 O 的直径,则 ACB是直角.
三、圆内接多边形
1.圆内接多边形:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这
个圆叫做多边形的外接圆.
2.圆内接四边形的性质:
第 8讲 圆的基本定理
\ 10 /
(1)性质 1:圆内接四边形的对角互补.
(2)性质 2:圆内接四边形的任意一个外角等于它的内对角.
D
A
O
E
C
B
如图,点 A、B、C、D 都在圆上,则 A BCD 180 , B D 180 , DCE A .
【经典例题】
【例7】
1.如图,在 O 中, AB AC,若 ABC 57.5 ,则弦 BC 所对的圆周角的度数为____________.
【解答】解: AB AC , ABC 57.5 ,
ACB ABC 57.5 ,
A 180 ABC ACB 65 ,
65 或115
2.(互动 5)如图, M 过点O(0,0) , A( 3 , 0) ,B(0,1),点C 是 x 轴上方弧 AB 上的一点,连
接 BC ,CO,则 BCO的度数是 ( )
A.15 B.30 C. 45 D.60
【解答】解:连接 AB ,如图,
A( 3 , 0) , B(0,1),
第 8讲 圆的基本定理
\ 11 /
OA 3 ,OB 1,
OB 1 3
tan BAO ,
OA 3 3
BAO 30 ,
BCO 30 .
故选: B .
【例8】
1.(互动 6)如图,在 ABC 中, AB AC.以 AB 为直径作半圆O,交 BC 于点 D ,交 AC 于点
E ,若 C 70 ,则 ABE 的度数是 ( )
A.50 B. 65 C. 70 D.80
【解答】解: AB AC , C 70 ,
BAC 40 ,
AB 是直径,
BAE ABE 90 ,
ABE 90 BAE 90 40 50 ,
故选: A .
第 8讲 圆的基本定理
\ 12 /
2.(互动 7)如图,矩形 ABCD 中, AB 3 , BC 8 ,点 P 为矩形内一动点,且满足
PBC PCD,则线段 PD的最小值为 ( )
A.5 B.1 C.2 D.3
【解答】解: 四边形 ABCD为矩形,
BCD 90 ,
PBC PCD,
PBC PCB 90 ,
BPC 90 ,
点 P 在以BC为直径的 O 上,
连接OD交 O 于 P ,连接OP 、 PD,如图,
PD OD OP(当且仅当O、 P 、 D 共线时,取等号),
即 P 点运动到 P 位置时, PD的值最小,最小值为DP ,
1
在Rt OCD中,OC BC 4,CD AB 3,
2
OD 32 42 5,
DP OD OP 5 4 1,
线段 PD的最小值为 1.
故选: B .
【例9】
如图,两圆 O 和 O 相交于 A 、 B1 2 两点, DBC 和 EAO1都是直线,且 AO1C 140 ,那么 E
110 度.
第 8讲 圆的基本定理
\ 13 /
【解答】解:连接 AB , E 110 .
【例10】
如图,在 O 中,直径 AB 10 ,弦 AC 6, ACB 的平分线交 O 于点D .
求 BC , AD , BD的长.
【解答】解: AB 是直径
ACB ADB 90
在Rt ABC中, AB2 AC2 BC2 , AB 10cm, AC 6cm
BC2 AB2 AC2 102 62 64
BC 64 8(cm)
又 CD平分 ACB,
AD BD ,
AD BD,
又 在 2 2 2Rt ABD中, AD BD AB
AD2 BD2 102
100
AD BD 5 2(cm).
2
第 8讲 圆的基本定理
\ 14 /
【例11】
研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图 1,已知
四边形 ABCD内接于 O ,对角线 AC BD,且 AC BD.
(1)求证: AB CD;
(2)若 O 的半径为 8,弧 BD的度数为120 ,求四边形 ABCD的面积;
(3)如图 2,作OM BC 于 M ,请猜测OM 与 AD 的数量关系,并证明你的结论.
【解答】(1)证明: AC BD,
AC BD ,
则 AB DC ,
AB CD;
(2)解:连接OB 、OD,作OH BD于H ,
弧 BD的度数为120 ,
BOD 120 ,
BOH 60 ,
3
则 BH OB 4 3 ,
2
BD 8 3 ,
1
则四边形 ABCD的面积 AC BD 96;
2
(3) AD 2OM ,
连结OB 、OC 、OA、OD,作OE AD于 E ,如图 2,
OE AD,
第 8讲 圆的基本定理
\ 15 /
AE DE ,
BOC 2 BAC ,
而 BOC 2 BOM ,
BOM BAC,
同理可得 AOE ABD,
BD AC,
BAC ABD 90 ,
BOM AOE 90 ,
BOM OBM 90 ,
OBM AOE ,
在 BOM 和 OAE中,
OMB OEA
OBM OAE ,
OB OA
BOM OAE ,
OM AE ,
AD 2OM .
备选题
【备1】
如图, O 与矩形 ABCD 的边 AB 、 CD 分别相交于点 E 、 F 、 G 、 H ,若 AE CH 6 ,则
BG DF为 6 .
【解答】解:作OM GH 于 M ,OM 交 EF 于 N ,如图,
EF / /GH ,
第 8讲 圆的基本定理
\ 16 /
OM EF ,
EN FN ,GM HM ,
易得四边形 ABMN 和四边形MNDC 为矩形,
AN BM , DN CM ,
BG DF BM GM DN NF
AN HM CM EN
AN EN CM HM
AE CH
6.
故答案为 6.
【备2】
如图,在 O 中,弦 AB 8,点C 在 AB 上移动,连接OC ,过点C 作CD OC 交 O 于点 D ,则
CD的最大值是 ( )
A.2 B.4 C.6 D.8
【解答】解:作OH AB于 H ,连接OA、OD,如图,
1 1
AH BH AB 8 4,
2 2
CD OC ,
CD OD2 OC2 ,
而OD为定值,OC 最小时,CD最大,
当OC OH 时,CD的值最大,
CD的最大值为 4.
故选: B .
第 8讲 圆的基本定理
\ 17 /
第 8讲 圆的基本定理
\ 18 /
挑战极限
如图, AB 是 O 的直径,C、D 为圆上两点,且 OAC 30 ,OD 绕着点O 顺时针旋转,连结
CD交直线 AB 于点 E ,当DE OD时, OCE的大小可能为_________________.
【原题】如图, AB 是 O 的直径,点C , D 在 O 上,且 OAC 30 ,OD绕着点O顺时针旋转,
连结CD交直线 AB 于点 E ,当 DE OD时, OCE的大小可能为 ( )
A. 20 B. 70 C.80 D.20 、 40 或80
【解答】解:
连接OC ,
①如图 1,OD绕着点O顺时针旋转,连结CD交直线 AB 于点 E ,
设 OCE x,
OC OD,
OCE D x,
OA OC,
OCA A 30 ,
DE OD,
DOE DEO 30 x 30 60 x
第 8讲 圆的基本定理
\ 19 /
2(60 x) x 180
解得 x 20 .
OCE 的大小为20 ;
②如图 2,
设 OEC x,
DE OD,
EOD E x,
DO CO,
ODC OCD 2x,
EOC 2 A 60
在 OCE 中,
x 60 2x 180 ,
解得 x 40 ,
OCE 2x 80 ;
③如图 3,
设 ACE x,
OA OC,
OCA OAC 30 ,
OC OD,
OCD ODC 30 x,
OD DE
第 8讲 圆的基本定理
\ 20 /
1 1
E ODC 15 x ,
2 2
1
15 x x 30
2
解得 x 10 ,
OCE 30 x 40 .
综上: OCE的大小为:20 、 40 、80 .
故选:D.
第 8讲 圆的基本定理
\ 21 /
巩固练习
【练习1】
1.如图, ABC 内接于 O ,若 A 45 ,OC 2,则 BC 的长为 ( )
A. 2 B. 2 2 C. 2 3 D.4
【解答】解:由圆周角定理得, BOC 2 A 90 ,
BC 2OC 2 2 ,
故选: B .
2.如图,已知 A 、 B 、C 、 D 、 E 均在 O 上,且 AC 为 O 的直径,则 A B C 的度数为
( )
A. 45 B. 60 C.90 D.120
【解答】解: AC 为 O 的直径,
AE ED CD的度数是180 ,
A B C 90 ,
故选:C .
【练习2】
如图,一把直角三角板的顶点 A 、 B 在 O 上,边 BC 、 AC 与 O 交于点 D 、 E ,已知 C 30 ,
AED的大小为 ( )
A.90 B.100 C.110 D.120
第 8讲 圆的基本定理
\ 22 /
【解答】解: A 90 , C 30 ,
B 90 30 60 ,
四边形 ABDE 是圆内接四边形,
AED 180 B 120 ,
故选:D .
【练习3】
如图,已知 AB 是 O 的直径,弦 CD 交 AB 于点 E , CEA 30 , OF CD ,垂足为点 F ,
DE 5,OF 1,那么CD 10 2 3 .
【解答】解: AB 是 O 的直径,OF CD,
根据垂径定理可知:
CF DF ,
CEA 30 ,
OEF 30 ,
OE 2, EF 3 ,
DF DE EF 5 3 ,
CD 2DF 10 2 3 .
故答案为:10 2 3 .
【练习4】
如图, O 的弦 AB 、DC的延长线相交于点 E .
(1)如图 1,若 AD 为120 , BC 为50 ,求 E 的度数;
(2)如图 2,若 AB CD,求证: AE DE .
第 8讲 圆的基本定理
\ 23 /
【解答】(1)解:连接 AC .
弧 AD 为120 ,弧 BC 为50 ,
ACD 60 , BAC 25 ,
ACD BAC E
E ACD BAC 60 25 35 ;
(2)证明:连接 AD .
AB CD,
弧 AB 弧CD,
弧 AC 弧 BD,
ADC DAB ,
AE DE .
【练习5】
如图, MB, MD 是 O 的两条弦,点 A ,C 分别在MB,MD 上,且 AB CD,M 是 AC 的中点.
(1)求证:MB MD ;
(2)过O作OE MB于点 E ,当OE 1,MD 4时,求 O 的半径.
【解答】(1)证明: AB CD,
AB CD ,
M 是 AC 的中点,
第 8讲 圆的基本定理
\ 24 /
AM CM ,
BM DM ,
BM DM .
(2)解:如图,连接OM .
DM BM 4,OE BM ,
EM BE 2 ,
OE 1, OEM 90 ,
OM OE2 EM 2 12 22 5 ,
O的半径为 5 .
第 8讲 圆的基本定理
\ 25 /
