苏科版八年级数学下册 第9章中心对称图形—平行四边形 小结与思考 课件 (共34张PPT)
文档属性
| 名称 | 苏科版八年级数学下册 第9章中心对称图形—平行四边形 小结与思考 课件 (共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 856.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 07:48:37 | ||
图片预览



文档简介
(共34张PPT)
小结与思考
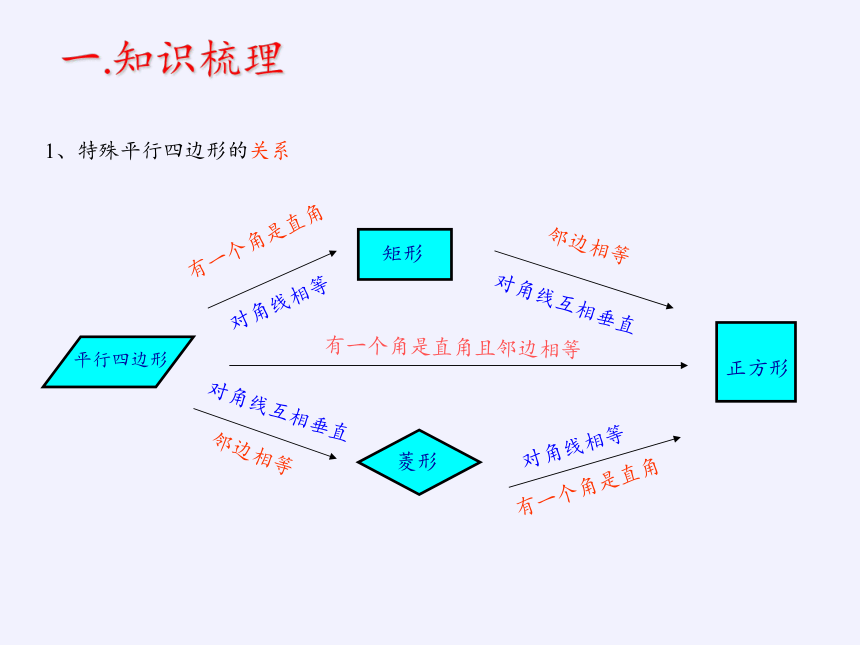
1、特殊平行四边形的关系
平行四边形
矩形
菱形
正方形
有一个角是直角
邻边相等
邻边相等
有一个角是直角
有一个角是直角且邻边相等
一.知识梳理
对角线相等
对角线互相垂直
对角线相等
对角线互相垂直
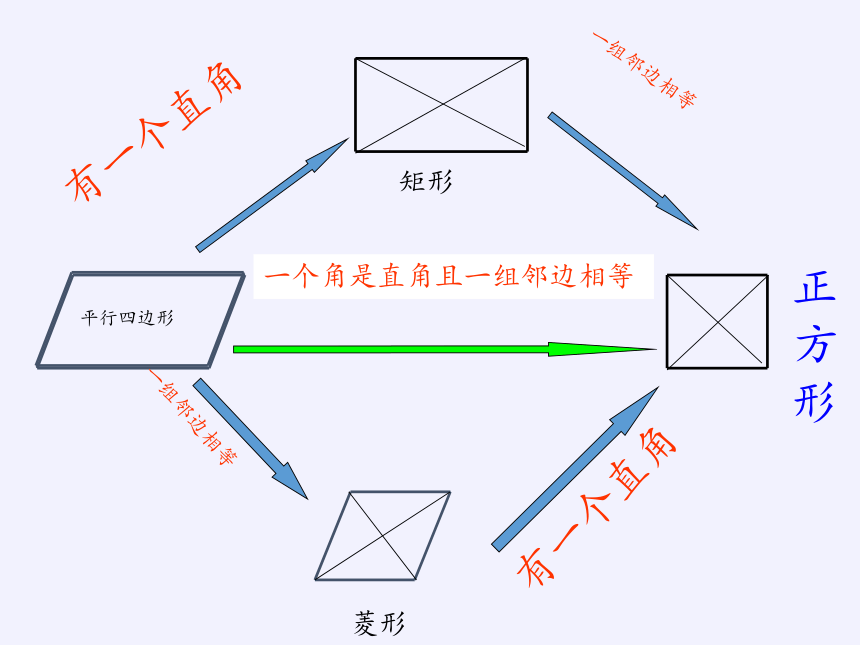
有一个直角
一组邻边相等
一组邻边相等
有一个直角
一个角是直角且一组邻边相等
正方形
平行四边形
矩形
菱形
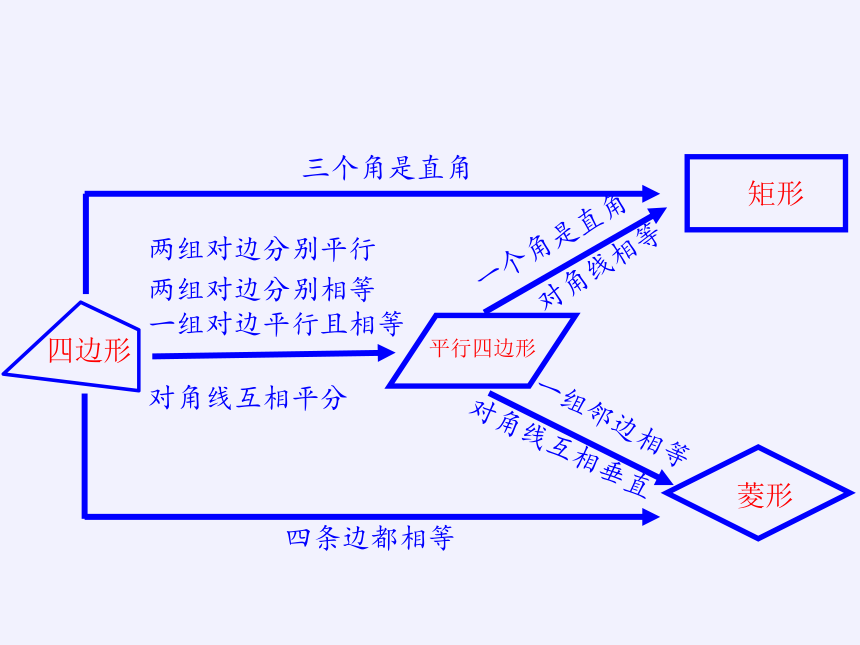
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
两组对边分别相等
一组对边平行且相等
对角线互相平分
平行四边形
矩形
菱形
四边形
矩形
平行四边形
四边形
菱形
正方形
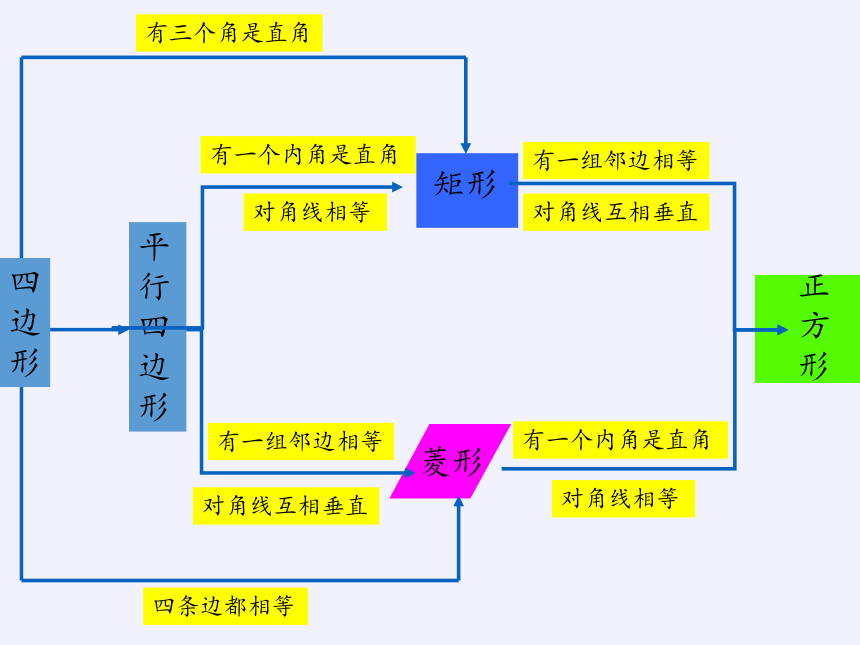
有一个内角是直角
对角线相等
有一组邻边相等
对角线互相垂直
四条边都相等
有三个角是直角
有一组邻边相等
对角线互相垂直
有一个内角是直角
对角线相等
项目 四边形 对边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
平行且相等
对角相等
邻角互补
互相平分
中心对称图形
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分,且每一条对角线平分一组对角
互相垂直平分且相等,每一条对角线平分一组对角
中心对称图形
轴对称图形
中心对称图形
轴对称图形
中心对称图形
轴对称图形
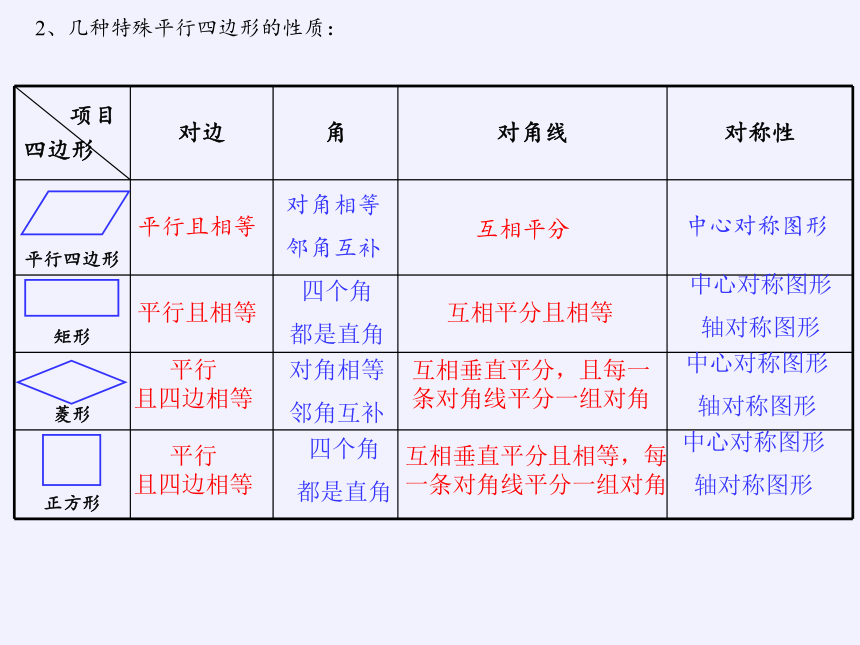
2、几种特殊平行四边形的性质:
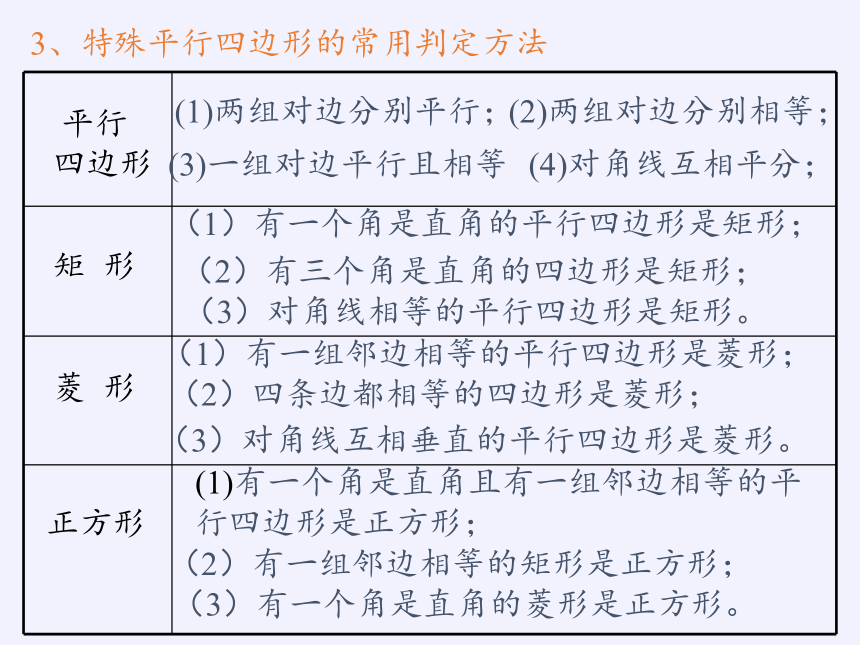
3、特殊平行四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(4)对角线互相平分;
(3)一组对边平行且相等
矩 形
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
识图悟法
问题1:已知:E、F是平行四边形ABCD对角线 AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
判定方法
1. 定义判定法。
2. 一组对边平行且相等的四
边形是平行四边形
3. 两组对边相等的四边形是
平行四边形。
4. 对角线互相平分的四边形
是平行四边形。
判定方法
1、一组邻边相等 + 平行四边
形=菱形
2. 四条边都相等的四边形是
菱形。
3. 对角线互相垂直的平行四边
形是菱形。
问题2:已知:E、F是正方形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BEDF是什么特殊的四边形
O
识图悟法
问题3:如图,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于O,将纸△ABC沿对角线AC翻折,
得到△AB′C,问以A、C、D、B′为顶点的四边形是什么形状的四边形?证明你的结论.
判定方法
1. 90°+ 平行四边形=矩形
2. 有三个角是直角的四边
形是矩形。
3. 对角线相等的平行四
边形是矩形。
D为任意△ABC的边边上的任意一点,过D分别作DE∥AC, DF ∥AB,那么,四边形AEDF是什么四边形?
A
C
B
D
F
E
问题4:想一想
思考2:再添上一个条件:∠ BAC=90°呢?四边形AEDF是什么四边形?
思考1: AD为任意△ABC的角平分线,四边形AEDF是什么四边形?
1
2
3
C
D
F
E
B
A
∟
问题5:如图,菱形ABCD的对角线AC、BD相交于点O,分别延长OA、OC到点E、F,使AE=CF,依次连接B、F、D、E各点.(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA=_______°时,
四边形BFDE是正方形.
判定:1. 定义判定法:
一个角为直角 + 一组邻边相等
+ 平行四边形
= 正方形
2. 一组邻边相等 + 矩形 = 正方形
3. 一角为90°+ 菱形 = 正方形
问题2:(1)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°, 若 对角线AC=4cm,则你能求出什么?
A
B
C
D
O
特殊平行四边形转化为特殊三角形
角
边
周长
面积
菱形、正方形的面积等于它的两条对角线乘积的一半.
B
A
D
C
O
二.巩固知识
方法:
面积:
(2)如图,菱形的对角线AC、BD的长分别为了4cm、6cm,则菱形的面积是多少?
问题3:如图在边长为2的菱形ABCD中, ∠ABC=60°,F是对角线BD上的动点.
E
三.知识升华
(1)求AF+CF的最小值.
(2)如果E是BC的中点求EF+CF的最小值.
B
A
C
D
F
A
B
C
D
E
F
问题3:边长为2的菱形ABCD中, ∠ABC=60°,点E是BC的中点,F是BD上的动点,求EF+CF的最小值.
A
B
C
D
E
F
E′
问题3:边长为2的菱形ABCD中, ∠ABC=60°,点E是BC的中点,F是BD上的动点,求EF+CF的最小值.
如图1:正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,连接EB,过点A作AM⊥BE,垂足M,AM交BD于点F
四. 拓展提高
(2)如果点E在AC的延长线上,AM⊥EB的延长线于点M,交DB的延长线于点F,其他条件都不变,则结论“OE=OF”还成立吗?
(1)试判断OE与OF大小关系,并说明理由?
A
图1
F
∟
M
A
B
C
D
E
O
图2
B
C
D
O
F
E
M
∟
五. 分享收获
1、通过本节课的学习你对特殊平行四边形之间的关系更深刻了吗?
2、你体验到利用特殊平行四边形的性质与判定解决问题时的策略了吗?
1、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF。则∠CDF等于( )
A.80° B.70° C.65° D.60°
练一练
D
2、用两个边长为a的等边三角形纸片拼成的四边形是 ( )
A.等腰梯形 B.正方形
C.矩形 D.菱形
D
3、下列命题中,是真命题的是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直且相等的四边形是正方形
C
4.菱形的一边和等腰直角三角形的一直角边等长,若菱形有一个角为30°,则菱形的面积与三角形的面积之比是 ( )
A.1∶2 B.1∶1.5 C.1∶1 D.3∶4
C
5.正方形具有而菱形不一定具有的性质是( )
A.四边相等 B.对角线垂直且平分
C.对角线相等 D.对角线平分一组对角
C
祝同学们学业进步,收获多多!
再 见 !
基础 + 方法 = 能力!
谢 谢
小结与思考
1、特殊平行四边形的关系
平行四边形
矩形
菱形
正方形
有一个角是直角
邻边相等
邻边相等
有一个角是直角
有一个角是直角且邻边相等
一.知识梳理
对角线相等
对角线互相垂直
对角线相等
对角线互相垂直
有一个直角
一组邻边相等
一组邻边相等
有一个直角
一个角是直角且一组邻边相等
正方形
平行四边形
矩形
菱形
三个角是直角
四条边都相等
一个角是直角
对角线相等
一组邻边相等
对角线互相垂直
两组对边分别平行
两组对边分别相等
一组对边平行且相等
对角线互相平分
平行四边形
矩形
菱形
四边形
矩形
平行四边形
四边形
菱形
正方形
有一个内角是直角
对角线相等
有一组邻边相等
对角线互相垂直
四条边都相等
有三个角是直角
有一组邻边相等
对角线互相垂直
有一个内角是直角
对角线相等
项目 四边形 对边 角 对角线 对称性
平行四边形
矩形
菱形
正方形
平行且相等
对角相等
邻角互补
互相平分
中心对称图形
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分,且每一条对角线平分一组对角
互相垂直平分且相等,每一条对角线平分一组对角
中心对称图形
轴对称图形
中心对称图形
轴对称图形
中心对称图形
轴对称图形
2、几种特殊平行四边形的性质:
3、特殊平行四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(4)对角线互相平分;
(3)一组对边平行且相等
矩 形
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
识图悟法
问题1:已知:E、F是平行四边形ABCD对角线 AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形
判定方法
1. 定义判定法。
2. 一组对边平行且相等的四
边形是平行四边形
3. 两组对边相等的四边形是
平行四边形。
4. 对角线互相平分的四边形
是平行四边形。
判定方法
1、一组邻边相等 + 平行四边
形=菱形
2. 四条边都相等的四边形是
菱形。
3. 对角线互相垂直的平行四边
形是菱形。
问题2:已知:E、F是正方形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BEDF是什么特殊的四边形
O
识图悟法
问题3:如图,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于O,将纸△ABC沿对角线AC翻折,
得到△AB′C,问以A、C、D、B′为顶点的四边形是什么形状的四边形?证明你的结论.
判定方法
1. 90°+ 平行四边形=矩形
2. 有三个角是直角的四边
形是矩形。
3. 对角线相等的平行四
边形是矩形。
D为任意△ABC的边边上的任意一点,过D分别作DE∥AC, DF ∥AB,那么,四边形AEDF是什么四边形?
A
C
B
D
F
E
问题4:想一想
思考2:再添上一个条件:∠ BAC=90°呢?四边形AEDF是什么四边形?
思考1: AD为任意△ABC的角平分线,四边形AEDF是什么四边形?
1
2
3
C
D
F
E
B
A
∟
问题5:如图,菱形ABCD的对角线AC、BD相交于点O,分别延长OA、OC到点E、F,使AE=CF,依次连接B、F、D、E各点.(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA=_______°时,
四边形BFDE是正方形.
判定:1. 定义判定法:
一个角为直角 + 一组邻边相等
+ 平行四边形
= 正方形
2. 一组邻边相等 + 矩形 = 正方形
3. 一角为90°+ 菱形 = 正方形
问题2:(1)如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°, 若 对角线AC=4cm,则你能求出什么?
A
B
C
D
O
特殊平行四边形转化为特殊三角形
角
边
周长
面积
菱形、正方形的面积等于它的两条对角线乘积的一半.
B
A
D
C
O
二.巩固知识
方法:
面积:
(2)如图,菱形的对角线AC、BD的长分别为了4cm、6cm,则菱形的面积是多少?
问题3:如图在边长为2的菱形ABCD中, ∠ABC=60°,F是对角线BD上的动点.
E
三.知识升华
(1)求AF+CF的最小值.
(2)如果E是BC的中点求EF+CF的最小值.
B
A
C
D
F
A
B
C
D
E
F
问题3:边长为2的菱形ABCD中, ∠ABC=60°,点E是BC的中点,F是BD上的动点,求EF+CF的最小值.
A
B
C
D
E
F
E′
问题3:边长为2的菱形ABCD中, ∠ABC=60°,点E是BC的中点,F是BD上的动点,求EF+CF的最小值.
如图1:正方形ABCD的对角线AC、BD相交于点O,E是AC上的一点,连接EB,过点A作AM⊥BE,垂足M,AM交BD于点F
四. 拓展提高
(2)如果点E在AC的延长线上,AM⊥EB的延长线于点M,交DB的延长线于点F,其他条件都不变,则结论“OE=OF”还成立吗?
(1)试判断OE与OF大小关系,并说明理由?
A
图1
F
∟
M
A
B
C
D
E
O
图2
B
C
D
O
F
E
M
∟
五. 分享收获
1、通过本节课的学习你对特殊平行四边形之间的关系更深刻了吗?
2、你体验到利用特殊平行四边形的性质与判定解决问题时的策略了吗?
1、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连接DF。则∠CDF等于( )
A.80° B.70° C.65° D.60°
练一练
D
2、用两个边长为a的等边三角形纸片拼成的四边形是 ( )
A.等腰梯形 B.正方形
C.矩形 D.菱形
D
3、下列命题中,是真命题的是( )
A.有两边相等的平行四边形是菱形
B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形
D.两条对角线互相垂直且相等的四边形是正方形
C
4.菱形的一边和等腰直角三角形的一直角边等长,若菱形有一个角为30°,则菱形的面积与三角形的面积之比是 ( )
A.1∶2 B.1∶1.5 C.1∶1 D.3∶4
C
5.正方形具有而菱形不一定具有的性质是( )
A.四边相等 B.对角线垂直且平分
C.对角线相等 D.对角线平分一组对角
C
祝同学们学业进步,收获多多!
再 见 !
基础 + 方法 = 能力!
谢 谢
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
