六年级下册数学第三单元圆柱与圆锥整理和复习课件(共31张PPT)
文档属性
| 名称 | 六年级下册数学第三单元圆柱与圆锥整理和复习课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 16:40:23 | ||
图片预览





文档简介
(共31张PPT)
圆柱与圆锥整理和复习
资料整理:
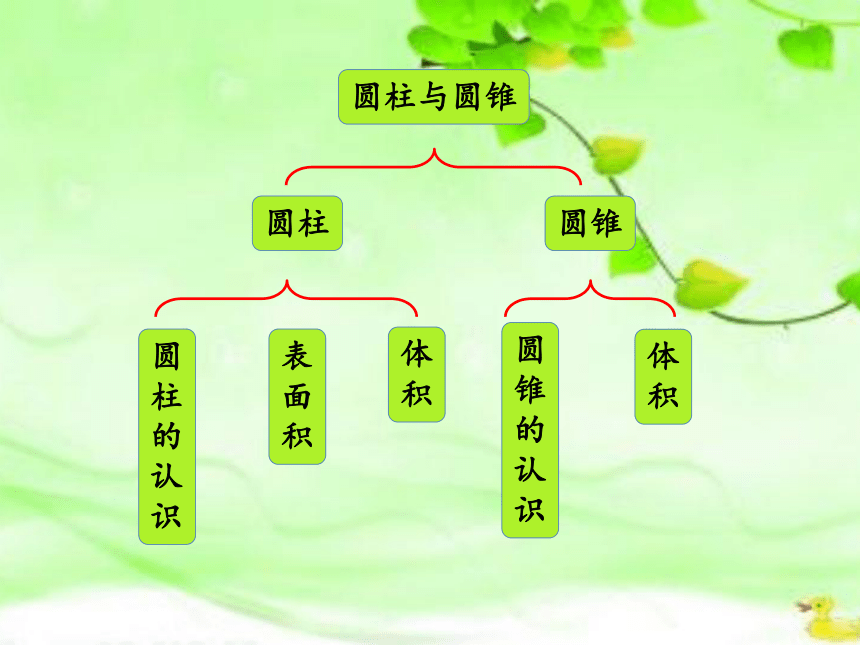
圆柱与圆锥
圆柱
圆锥
圆
柱
的
认
识
表
面
积
体
积
圆
锥
的
认
识
体
积
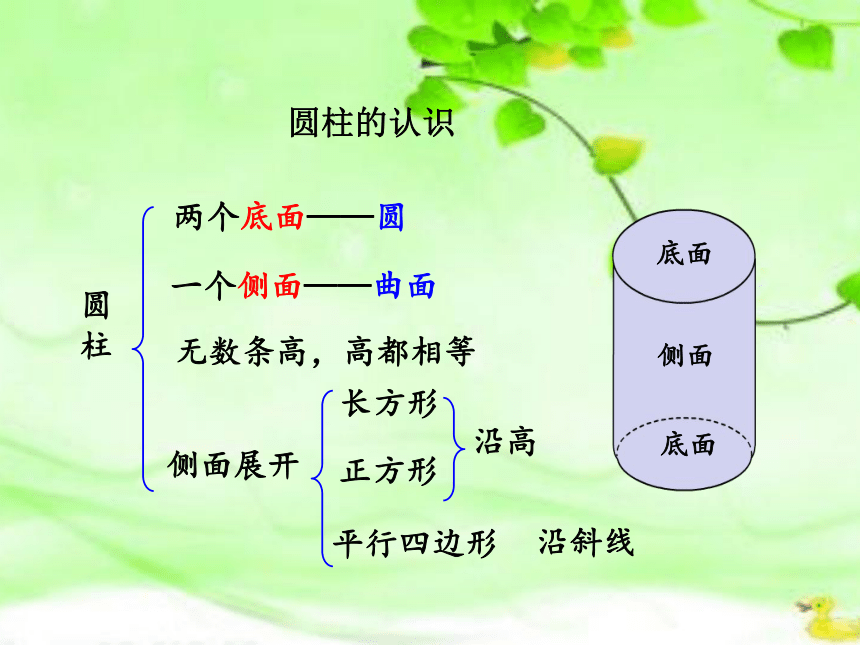
圆柱
两个底面——圆
圆柱的认识
底面
底面
侧面
一个侧面——曲面
无数条高,高都相等
侧面展开
长方形
正方形
平行四边形
沿高
沿斜线
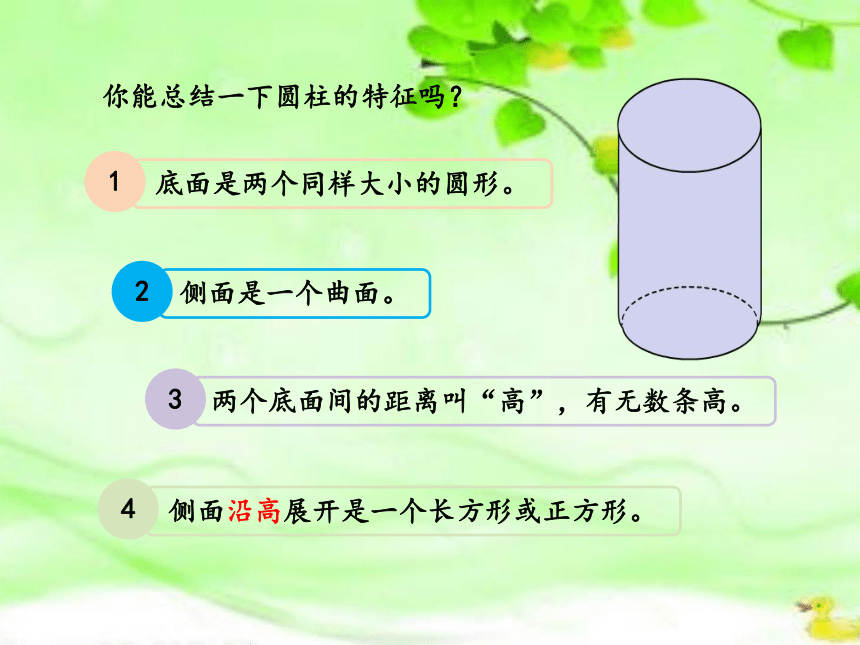
你能总结一下圆柱的特征吗?
1
底面是两个同样大小的圆形。
2
侧面是一个曲面。
3
两个底面间的距离叫“高”,有无数条高。
4
侧面沿高展开是一个长方形或正方形。
判断对错。
1.圆柱的高只有一条。 ( )
2.圆柱两个底面的直径相等。 ( )
3. 圆柱的底面周长和高相等时,展开后的侧面一定是个长方形。 ( )
圆柱的变面积
圆柱的侧面积=底面周长×高
S侧 = Ch
圆柱的表面积=侧面积 + 两个底面的面积
S表 = S侧 + 2S底
= 2 rh + 2 r2
要根据具体情况计算表面积涉及哪几个面。
圆柱的侧面积和表面积
底面周长:C
高:h
半径:r
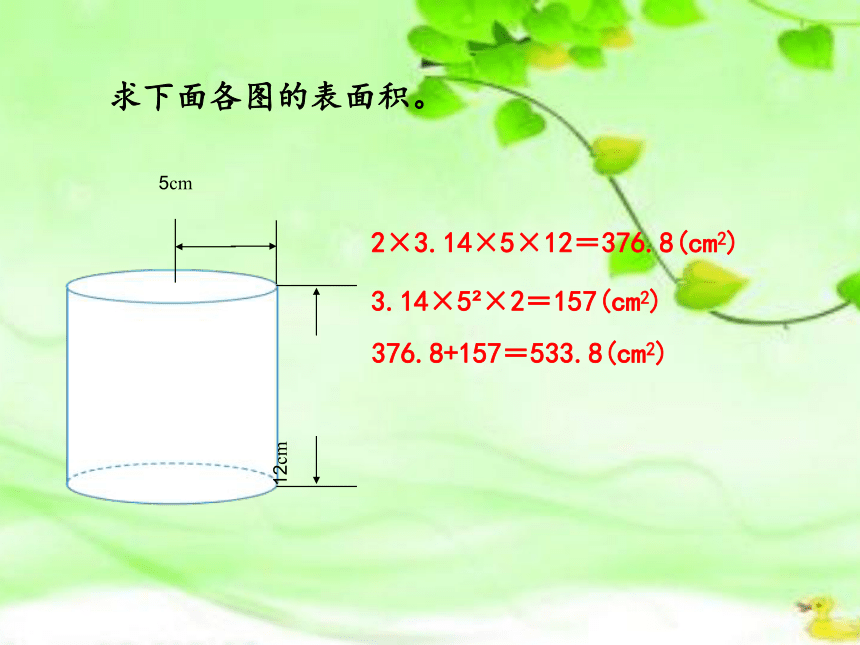
求下面各图的表面积。
5cm
12cm
2×3.14×5×12=376.8(cm2)
3.14×5 ×2=157(cm2)
376.8+157=533.8(cm2)
求下面各圆柱的侧面积。
1.6×0.7=1.12(平方米)
(1)底面周长是1.6m,高是0.7m。
(2)底面半径是3.2dm,高5dm。
圆柱侧面积=底面周长×高
圆柱侧面积=2r×高
2×3.14×3.2×5=100.48(平方分米)
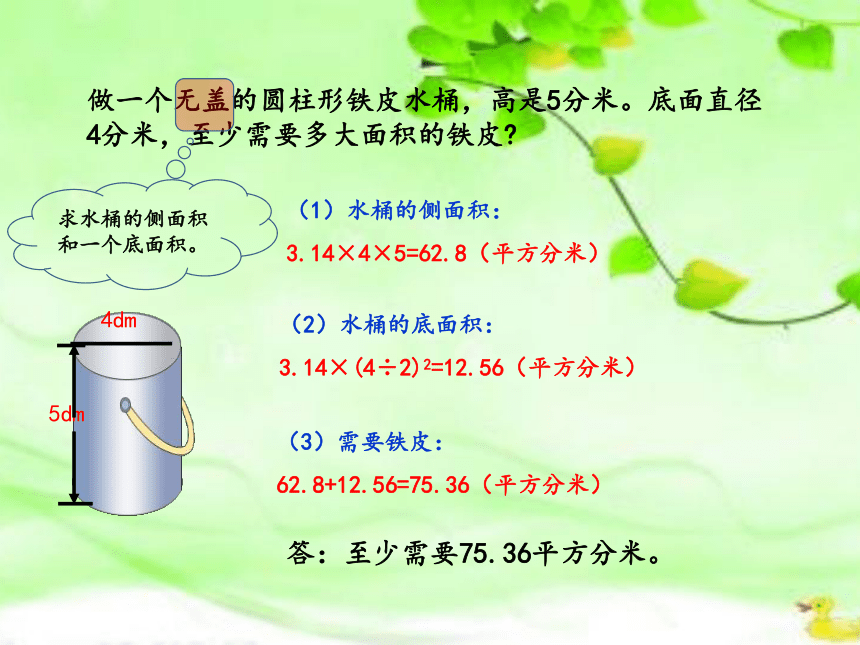
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮
(1)水桶的侧面积:
3.14×4×5=62.8(平方分米)
(2)水桶的底面积:
3.14×(4÷2)2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
5dm
4dm
求水桶的侧面积和一个底面积。
答:至少需要75.36平方分米。
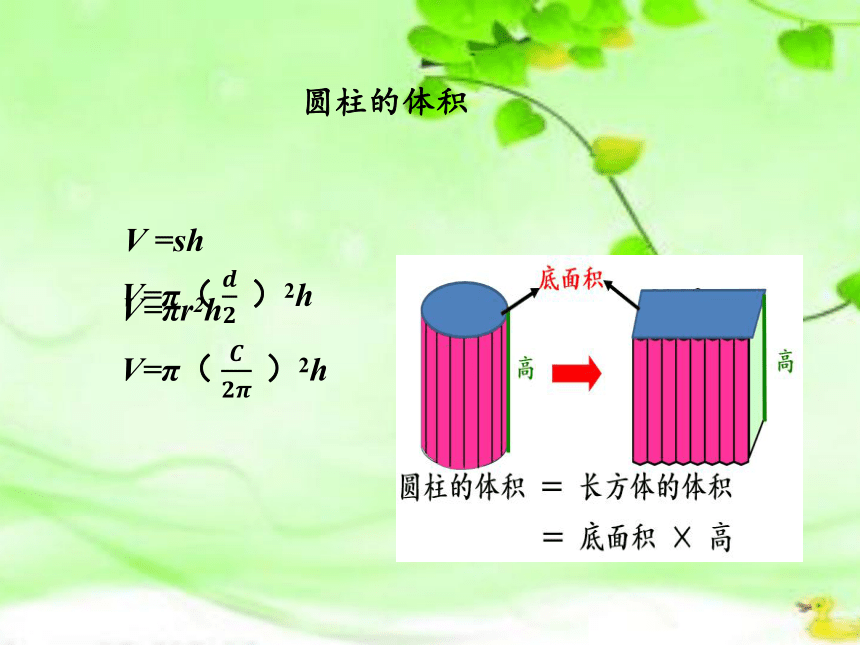
圆柱的体积
V=πr2h
V =sh
V=π( )2h
V=π( )2h
李家庄挖了一口圆柱形井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
已知底面直径和高求圆柱体积。
V=π( )2h
= 3.14×(1÷2)2×10
= 7.85(立方米)
答:挖出的土有7.85立方米。
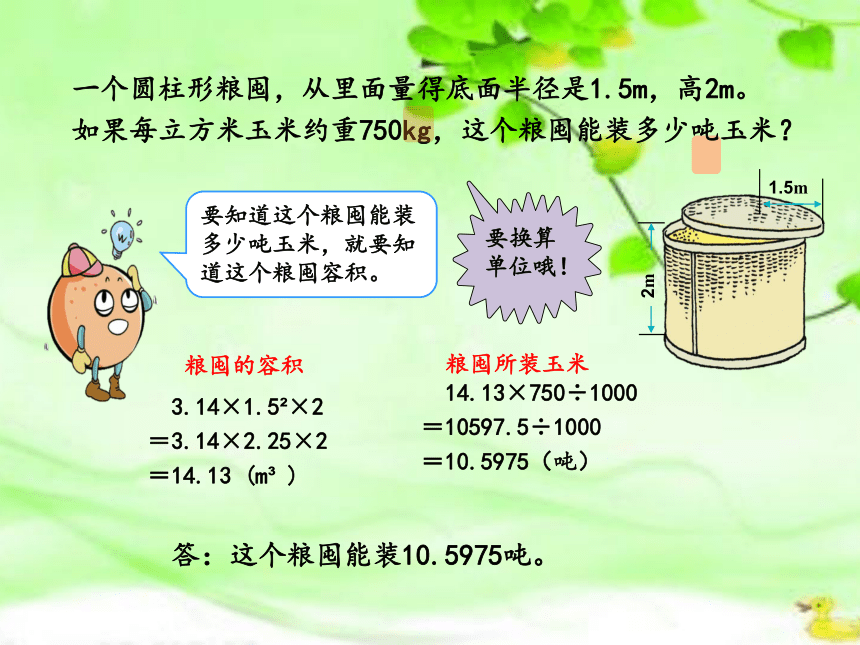
一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
3.14×1.5 ×2
=3.14×2.25×2
=14.13 (m )
14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
要知道这个粮囤能装多少吨玉米,就要知道这个粮囤容积。
1.5m
2m
粮囤所装玉米
粮囤的容积
要换算单位哦!
解决瓶子容积问题
1.瓶子容积=水的体积+空瓶子体积
2.将不规则图形转化成规则图形。
3.瓶子正放和倒置时空余部分的容积是相等的。
18cm
7cm
7cm
18cm
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
答:小明喝了282.6mL的水。
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm3)
=282.6(mL)
10cm
求这个矿泉水瓶的容积是多少?
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。
答:这个矿泉水瓶的容积是706.5mL。
3.14×(6÷2)2×(15+10 )
=3.14×9×25
=28.26×25
=706.5(cm )
=706.5(mL)
10cm
15cm
认识圆锥
面
底面
侧面
1个,圆形。
1个,曲面(展开是扇形)
高只有1条。
判断对错。
1.圆锥的高有无数条。 ( )
2.圆锥的底面是圆形的。 ( )
3.圆柱的侧面展开是长方形,圆锥的侧面
展开也是长方形。 ( )
圆锥的体积等于与它等底等高圆柱体积的。
圆锥的体积
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
Ⅴ = S h
锥
锥
锥
Ⅴ = S h
柱
柱
柱
S = S
柱
锥
Ⅴ = Ⅴ
柱
锥
h = 3h
柱
锥
判断对错。
圆柱的体积等于与它等底等高的圆锥的体积。
( )
2.圆柱的体积等于圆锥体积的三分之一。 ( )
3.圆柱的侧面展开是长方形,圆锥的侧面展开也是
长方形。 ( )
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
4m
1.5m
(1)沙堆的底面积:
3.14 ×(4÷2)2 =12.56(m2)
(3)沙堆的重量:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42t。
(2)沙堆的体积:
12.56 ×1.5 ×=6.28(m3)
答:这堆沙子大约6.28m3。
一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
=23.55(m )
×28.26×2.5
(1)沙堆的体积:
(2)所铺公路的长度:
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
=9.42×2.5
答:能铺117.75m。
2cm=0.02m
注意单位转换哦!
公园里有一座如图所示的房子,这座房子的体积是多少立方米?
3.14×(4÷2)2×2+3.14×(4÷2)2×1.5×
=31.4(m3)
答:这座房子的体积是31.4m3。
圆锥的体积
圆柱的体积
+
=25.12+6.2831.4
比较圆柱和圆锥
底面
侧面
高
只有一个
两个完全一样的圆
只有一条
有无数条
曲面,展开后是扇形。
曲面,沿高展开后是长方形(正方形)
小组交流:补全下面表格中的内容,并举手回答。
(1)把圆柱的侧面沿着一条高剪开,得到一个( ),它的一条边等于圆柱的( ),另一条边等于圆柱的( )。
(2)长方体、正方体、圆柱的体积计算公式都可以写成( )。
(3)一个圆柱,如果底面直径不变,高增加到原来的2倍,体积就增加到原来的( )倍;如果高和直径都增加到原来的2倍,体积就增加到原来的( )倍。
1.我会填。
(4)一个圆锥体的体积是31.4立方分米,高是5分米,它的底面积是( )平方分米。
(5)一个圆柱和一个圆锥的体积与高都相等,圆柱的底面积是6平方厘米,圆锥的底面积是( )平方厘米。
(6)一个装满水的圆锥形容器高9厘米,如果将水全部倒入一个与它等底等高的圆柱形容器中,则水高( )厘米。
2.我会选。(将正确答案的序号填在括号里)
(1)底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积,( )。
A.正方体体积大 B.长方体体积大
C.圆柱体体积大 D.一样大
(2)圆柱体的底面半径和高都扩大3倍,它的体积扩大( )倍。
A.3 B.6 C.9 D.27
(3)求圆柱形水杯能盛多少升水,就是求这个水杯的( )。
A.底面积 B.表面积 C.体积 D.容积
(1)圆柱和圆锥都有无数条高。 ( )
(2)两个圆柱的体积相等,它们的表面积也相等。 ( )
(3)圆柱的体积一定比与它等底等高圆锥的体积大。 ( )
(4)圆锥顶点到底面上一点的距离就是它的高。 ( )
3.我会判。(对的画“√”,错的画“ ”)
4.我会算。
(1)计算下面图形的表面积和体积。
(2)计算下面图形的体积。
5.解决问题。
某地新建一个圆柱形粮囤,从外面测,粮囤的直径为8米,高为6米。
(1)这个粮囤占地多少平方米
(2)现在要将粮囤外墙面全部粉刷成白色,粉刷面积是多少平方米
圆柱与圆锥整理和复习
资料整理:
圆柱与圆锥
圆柱
圆锥
圆
柱
的
认
识
表
面
积
体
积
圆
锥
的
认
识
体
积
圆柱
两个底面——圆
圆柱的认识
底面
底面
侧面
一个侧面——曲面
无数条高,高都相等
侧面展开
长方形
正方形
平行四边形
沿高
沿斜线
你能总结一下圆柱的特征吗?
1
底面是两个同样大小的圆形。
2
侧面是一个曲面。
3
两个底面间的距离叫“高”,有无数条高。
4
侧面沿高展开是一个长方形或正方形。
判断对错。
1.圆柱的高只有一条。 ( )
2.圆柱两个底面的直径相等。 ( )
3. 圆柱的底面周长和高相等时,展开后的侧面一定是个长方形。 ( )
圆柱的变面积
圆柱的侧面积=底面周长×高
S侧 = Ch
圆柱的表面积=侧面积 + 两个底面的面积
S表 = S侧 + 2S底
= 2 rh + 2 r2
要根据具体情况计算表面积涉及哪几个面。
圆柱的侧面积和表面积
底面周长:C
高:h
半径:r
求下面各图的表面积。
5cm
12cm
2×3.14×5×12=376.8(cm2)
3.14×5 ×2=157(cm2)
376.8+157=533.8(cm2)
求下面各圆柱的侧面积。
1.6×0.7=1.12(平方米)
(1)底面周长是1.6m,高是0.7m。
(2)底面半径是3.2dm,高5dm。
圆柱侧面积=底面周长×高
圆柱侧面积=2r×高
2×3.14×3.2×5=100.48(平方分米)
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮
(1)水桶的侧面积:
3.14×4×5=62.8(平方分米)
(2)水桶的底面积:
3.14×(4÷2)2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
5dm
4dm
求水桶的侧面积和一个底面积。
答:至少需要75.36平方分米。
圆柱的体积
V=πr2h
V =sh
V=π( )2h
V=π( )2h
李家庄挖了一口圆柱形井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
已知底面直径和高求圆柱体积。
V=π( )2h
= 3.14×(1÷2)2×10
= 7.85(立方米)
答:挖出的土有7.85立方米。
一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
3.14×1.5 ×2
=3.14×2.25×2
=14.13 (m )
14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
要知道这个粮囤能装多少吨玉米,就要知道这个粮囤容积。
1.5m
2m
粮囤所装玉米
粮囤的容积
要换算单位哦!
解决瓶子容积问题
1.瓶子容积=水的体积+空瓶子体积
2.将不规则图形转化成规则图形。
3.瓶子正放和倒置时空余部分的容积是相等的。
18cm
7cm
7cm
18cm
无水部分高为10cm圆柱的体积就是小明喝了的水的体积。
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。小明喝了多少水?
答:小明喝了282.6mL的水。
3.14×(6÷2)2×10
=3.14×9×10
=28.26×10
=282.6(cm3)
=282.6(mL)
10cm
求这个矿泉水瓶的容积是多少?
一瓶装满的矿泉水,小明喝了一些,把瓶盖拧紧后倒置放平,无水部分高10cm,内径是6cm。
答:这个矿泉水瓶的容积是706.5mL。
3.14×(6÷2)2×(15+10 )
=3.14×9×25
=28.26×25
=706.5(cm )
=706.5(mL)
10cm
15cm
认识圆锥
面
底面
侧面
1个,圆形。
1个,曲面(展开是扇形)
高只有1条。
判断对错。
1.圆锥的高有无数条。 ( )
2.圆锥的底面是圆形的。 ( )
3.圆柱的侧面展开是长方形,圆锥的侧面
展开也是长方形。 ( )
圆锥的体积等于与它等底等高圆柱体积的。
圆锥的体积
Ⅴ = Ⅴ =
圆锥
圆柱
Sh
一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
Ⅴ = S h
锥
锥
锥
Ⅴ = S h
柱
柱
柱
S = S
柱
锥
Ⅴ = Ⅴ
柱
锥
h = 3h
柱
锥
判断对错。
圆柱的体积等于与它等底等高的圆锥的体积。
( )
2.圆柱的体积等于圆锥体积的三分之一。 ( )
3.圆柱的侧面展开是长方形,圆锥的侧面展开也是
长方形。 ( )
工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的体积大约是多少?如果每立方米沙子重1.5t,这堆沙子大约重多少吨?
4m
1.5m
(1)沙堆的底面积:
3.14 ×(4÷2)2 =12.56(m2)
(3)沙堆的重量:
6.28×1.5=9.42(t)
答:这堆沙子大约重9.42t。
(2)沙堆的体积:
12.56 ×1.5 ×=6.28(m3)
答:这堆沙子大约6.28m3。
一个圆锥形沙堆,底面积是28.26m2,高是2.5m。用这堆沙在10m宽的公路上铺2cm厚的路面,能铺多少米?
=23.55(m )
×28.26×2.5
(1)沙堆的体积:
(2)所铺公路的长度:
23.55÷10÷0.02
=2.355÷0.02
=117.75(m)
=9.42×2.5
答:能铺117.75m。
2cm=0.02m
注意单位转换哦!
公园里有一座如图所示的房子,这座房子的体积是多少立方米?
3.14×(4÷2)2×2+3.14×(4÷2)2×1.5×
=31.4(m3)
答:这座房子的体积是31.4m3。
圆锥的体积
圆柱的体积
+
=25.12+6.2831.4
比较圆柱和圆锥
底面
侧面
高
只有一个
两个完全一样的圆
只有一条
有无数条
曲面,展开后是扇形。
曲面,沿高展开后是长方形(正方形)
小组交流:补全下面表格中的内容,并举手回答。
(1)把圆柱的侧面沿着一条高剪开,得到一个( ),它的一条边等于圆柱的( ),另一条边等于圆柱的( )。
(2)长方体、正方体、圆柱的体积计算公式都可以写成( )。
(3)一个圆柱,如果底面直径不变,高增加到原来的2倍,体积就增加到原来的( )倍;如果高和直径都增加到原来的2倍,体积就增加到原来的( )倍。
1.我会填。
(4)一个圆锥体的体积是31.4立方分米,高是5分米,它的底面积是( )平方分米。
(5)一个圆柱和一个圆锥的体积与高都相等,圆柱的底面积是6平方厘米,圆锥的底面积是( )平方厘米。
(6)一个装满水的圆锥形容器高9厘米,如果将水全部倒入一个与它等底等高的圆柱形容器中,则水高( )厘米。
2.我会选。(将正确答案的序号填在括号里)
(1)底面积和高均相等的正方体、长方体、圆柱相比较,它们的体积,( )。
A.正方体体积大 B.长方体体积大
C.圆柱体体积大 D.一样大
(2)圆柱体的底面半径和高都扩大3倍,它的体积扩大( )倍。
A.3 B.6 C.9 D.27
(3)求圆柱形水杯能盛多少升水,就是求这个水杯的( )。
A.底面积 B.表面积 C.体积 D.容积
(1)圆柱和圆锥都有无数条高。 ( )
(2)两个圆柱的体积相等,它们的表面积也相等。 ( )
(3)圆柱的体积一定比与它等底等高圆锥的体积大。 ( )
(4)圆锥顶点到底面上一点的距离就是它的高。 ( )
3.我会判。(对的画“√”,错的画“ ”)
4.我会算。
(1)计算下面图形的表面积和体积。
(2)计算下面图形的体积。
5.解决问题。
某地新建一个圆柱形粮囤,从外面测,粮囤的直径为8米,高为6米。
(1)这个粮囤占地多少平方米
(2)现在要将粮囤外墙面全部粉刷成白色,粉刷面积是多少平方米
