第四章 数量、位置的变化期末复习

第四章 数量、位置的变化 期末复习 2011-1-
主备人：金菊英 审核人：吴晓刚 班级 姓名
【学习目标】
熟练掌握平面直角坐标系中点的特征。
2、通过描点、连线、看图以及由点找坐标等过程，发展学生的数形结合意识，合作交流意识。
【学习重点、难点】平面直角坐标系中点的特征。
【知识要点回顾】
1、若点Ｐ（x，y）在
（1）第一象限，则x____0，y____0
（2）第二象限，则x____0，y____0
（3）第三象限，则x____0，y____0
（4）第四象限，则x____0，y____0
（5）x轴上，则x______，y______
（6）y轴上，则x________，y________
（7）原点上，则x________，y_________
2、点Ｐ（x，y）对称点的坐标特点：
①关于x轴对称的点的坐标特点： ②关于y轴对称的点的坐标特点：
③关于原点对称的点的坐标特点：
3、平面直角坐标系中的点和 是一一对应的；
4、点A（x , y）到x轴的距离是 ,到y轴的距离是 到原点的距离是
5、各象限角平分线上的坐标特点
一、三象限角平分线上的点（x，y）的特点是 。
二、四象限角平分线上的点（x，y）的特点是 。
【预习检测】
1、已知P点坐标为（2a+1，a-3），①点P在x轴上，则a= ； ②点P在y轴上，则a= ；
③点P在第三象限内，则a的取值范围是 。
2、点Ａ（２，３）到x轴的距离为 ；点Ｂ（－４，０）到y轴的距离为 ；点P(5,-12)到原点的距离是____，点C到x轴的距离为1，到y轴的距离为3，且在第三象限，则C点坐标是 。
4、已知a>0,那么点P(-a2-1,a+3)关于原点的对称点Q在第_______象限。
5、△ABC中BC边上的中点为M，把△ABC向左平移2个单位，再向上平移3个单位后，得到△A1B1C1的B1C1边上中点M1的坐标为（－1，0），则M点坐标为___________。
【例题精选】
例1、已知P点坐标为（2a+4，a-3）
①点P在x轴上，则a ； ②点P在y轴上，则a ；
③点P在第三象限内，则a ； ④点P在第四象限内，则a ；
⑤点P在一、三象限的角平分线上，则a ；
⑥点P在二、四象限的角平分线上，则a ；
例2、点A(0,-3)，点B(4,0),点C在x轴上，如果△ABC的面积为15，求点C的坐标.
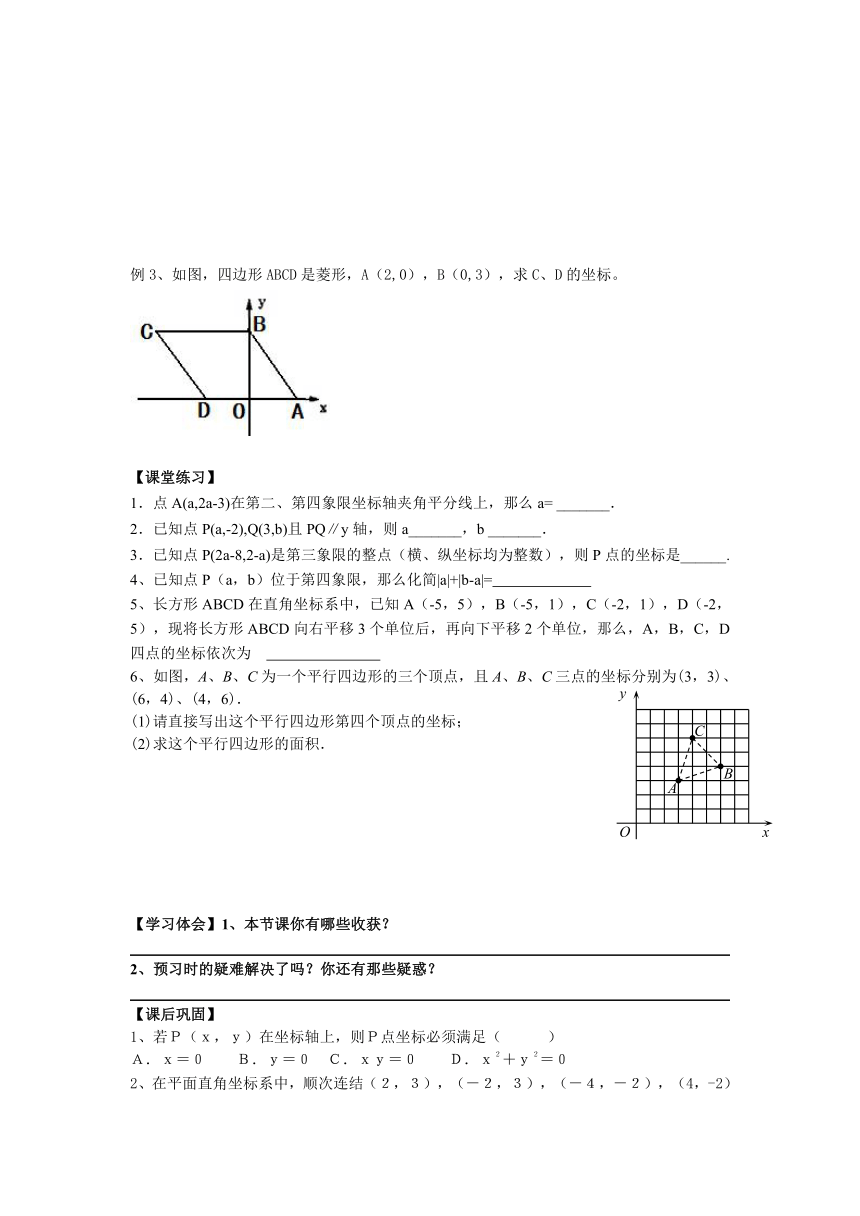
例3、如图，四边形ABCD是菱形，A（2,0），B（0,3），求C、D的坐标。
【课堂练习】
1．点A(a,2a-3)在第二、第四象限坐标轴夹角平分线上，那么a= _______．
2．已知点P(a,-2),Q(3,b)且PQ∥y轴，则a_______，b _______．
3．已知点P(2a-8,2-a)是第三象限的整点（横、纵坐标均为整数），则P点的坐标是______.
4、已知点P（a，b）位于第四象限，那么化简|a|+|b-a|=
5、长方形ABCD在直角坐标系中，已知A（-5，5），B（-5，1），C（-2，1），D（-2，5），现将长方形ABCD向右平移3个单位后，再向下平移2个单位，那么，A，B，C，D四点的坐标依次为
6、如图，A、B、C为一个平行四边形的三个顶点，且A、B、C三点的坐标分别为(3，3)、(6，4)、(4，6)．
(1)请直接写出这个平行四边形第四个顶点的坐标；
(2)求这个平行四边形的面积．
【学习体会】1、本节课你有哪些收获？

2、预习时的疑难解决了吗？你还有那些疑惑？

【课后巩固】
1、若Ｐ（ｘ，ｙ）在坐标轴上，则Ｐ点坐标必须满足（　　　）Ａ．ｘ＝０　　Ｂ．ｙ＝０　Ｃ．ｘｙ＝０　　Ｄ．ｘ２＋ｙ２＝０
2、在平面直角坐标系中，顺次连结（２，３），（－２，３），（－４，－２），（4，-2）所成的四边形是（　　　）Ａ．平行四形　　Ｂ．矩形　　Ｃ．菱形　　Ｄ．等腰梯形3、点Ｐ（ｍ＋３，ｍ＋１）在ｘ轴上，则Ｐ点坐标为（　　　）Ａ．（０，－４）　　Ｂ．（４，０）Ｃ．（０，－２）Ｄ．（２，０）
4、在平面直角坐标系中，当a﹤0时，点（a2，a）所在的象限是（ ） A、第一象限 B、第二象限 C、第三象限 D、第四象限
5、在直角坐标系中, 点在第一象限内, 且与轴正半轴的夹角为, 则的值是_ _；
6、已知平面直角坐标系中两点A(x，1)、B(一5，y)，(1)若点A、B关于x轴对称x=___ ,y=__；(2)若点A、B关于y轴对称，则x=__，y=__；(3)若点A、B关于原点对称，则x=___，y=___
7、已知点P(2m一5，m一1),(1)若点P在二、四象限的角平分线上，则m＝____； (2)若点P在一、三象限的角平分线上，则m＝____。
8、若点P（x，y）在第四象限，|x|=5，|y|=4，则P点的坐标为 。
9、若A（3，-5），AB∥x轴，且AB=2，则B点的坐标为 。
10、在平面直角坐标系中，点A（x，y），且xy=-2，试写出两个满足这些条件的点：________．
11、在平面直角坐标系中，点A（-1，1），将线段OA（O为坐标原点）绕点O逆时针旋转135°得线段OB，则点B的坐标是________．
12、在直角坐标系中，点A（0，2），点P（x，0）为x轴上的一个动点，当x=_______时，线段PA的长得到最小值，最小值是_________．
13、已知正方形ABCD在直角坐标系中,A（2，2），B（4，2），那么C点的坐标 ， D点的坐标为 。
14、一正三角形ABC，A(0，0)，B(－4，0)，C(－2，)，将三角形ABC绕原点顺时针旋转1200得到的三角形的三个顶点坐标分别是
15、点关于x轴的对称点Q的坐标为 ；P到y轴的距离为 ，到原点的距离为 。
16、如图，在正方形网格中，每个小正方形的边长均为1个
单位．将向下平移4个单位，得到，再把
绕点顺时针旋转，得到，请你画
出和（不要求写画法）．
17、如图中的图象(折线ABCDE)描述了一汽车在某一直路上的行驶过程中，汽车离出发地的距离s(千米)和行驶时间t(小时)之间的关系，根据图中提供的信息，求：①汽车共行驶了多少千米？②汽车在行驶途中停留了几小时？③汽车在整个行驶过程中的平均速度是多少？④汽车自出发后3小时至4.5小时之间行驶的速度是多少？
18、在平面直角坐标系内，A、B、C三点的坐标分别是A(5，0）、B（0，3）、C（5，3），O 为坐标原点，点E在线段BC上，若△AEO为等腰三角形, 求点E的坐标．（画出图象）
19、（2007湖州）在8×8的正方形网格中建立如图所示的平面直角坐标系，己知A（2，4），B（4，2）．C是第一象限内的一个格点，由点C与线段AB组成一个以AB为底，且腰长为无理数的等腰三角形，
（1）填空：C点的坐标是_________，△ABC的面积是__________；
（2）将△ABC绕点C旋转180°得到△A1B1C，连结AB1，BA1，试判断四边形AB1A1B是何种特殊四边形，请说明理由；
（3）请探究：在x轴上是否存在这样的点P，使以A、B、O、P为顶点的四边形的面积等于△ABC面积的2倍．若存在，请直接写出点P的坐标（不必写出解答过程）；若不存在，请说明理由．