2021-2022学年六年级下学期数学总复习第七课时《式与方程》(课件)(共24页)
文档属性
| 名称 | 2021-2022学年六年级下学期数学总复习第七课时《式与方程》(课件)(共24页) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
式 与 方 程
数学北师大版 六年级下
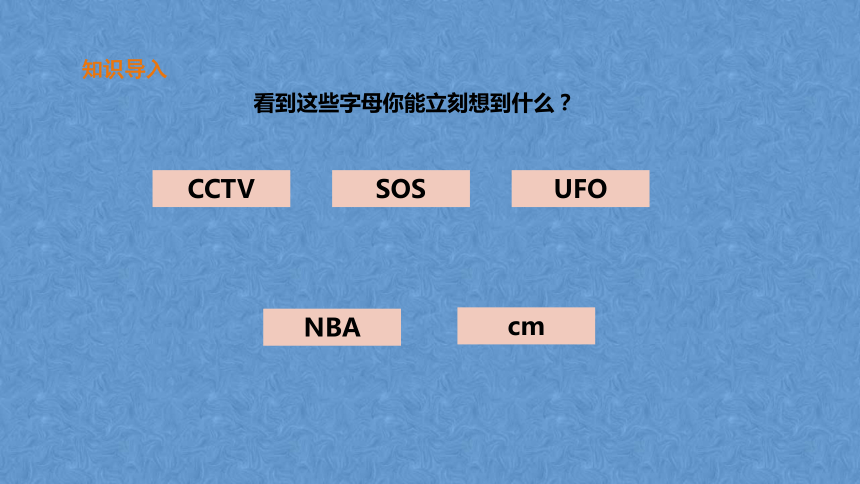
知识导入
看到这些字母你能立刻想到什么?
CCTV
SOS
UFO
NBA
cm
知识梳理----
用字母表示规律
1、(1)淘气利用圆片摆出下面的图案。
1×1
2×2
3×3
4×4
……
第n 个图案用多少个圆片?请你用含有字母的式子表示。
n×n=n
用字母表示数可以概括地表示规律。
知识梳理----
用字母表示规律。
(2)生活中还有哪些规律能利用这个式子表示?
一个边长是 ncm的正方形,面积是 n cm 。
一个方阵,每排n 人, 有n排,共有n 人。
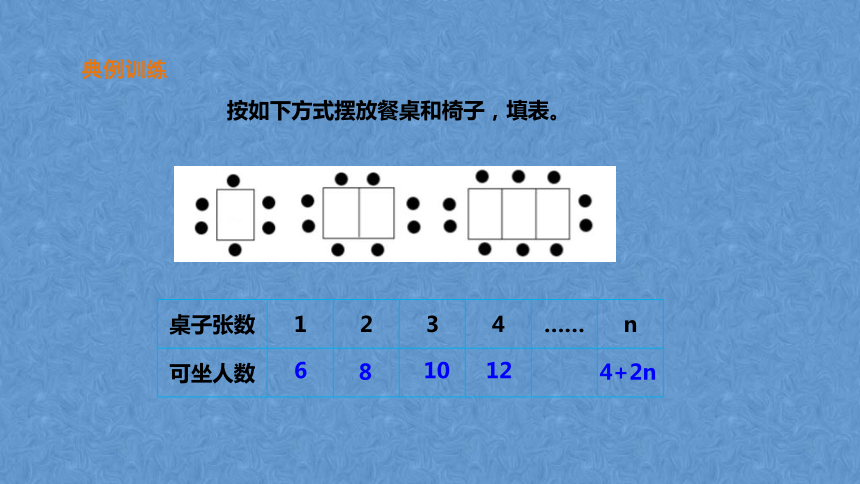
典例训练
按如下方式摆放餐桌和椅子,填表。
桌子张数 1 2 3 4 …… n
可坐人数
6
8
10
12
4+2n
知识梳理----
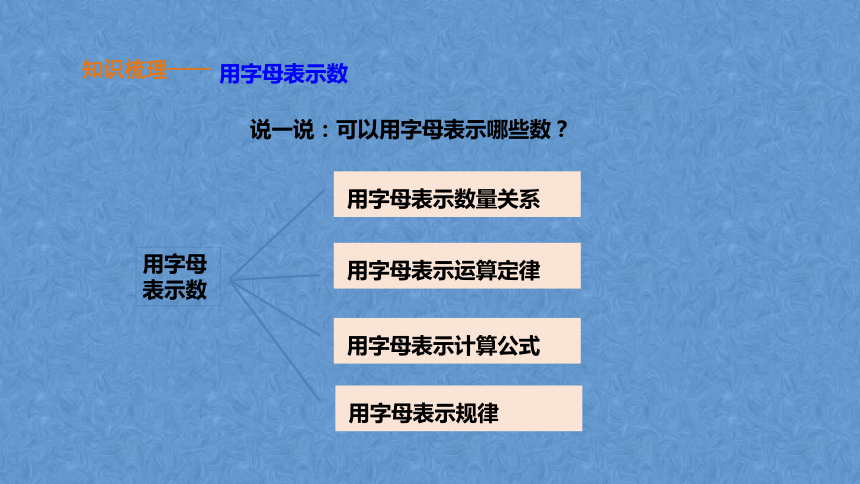
用字母表示数
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示规律
说一说:可以用字母表示哪些数?
知识梳理----
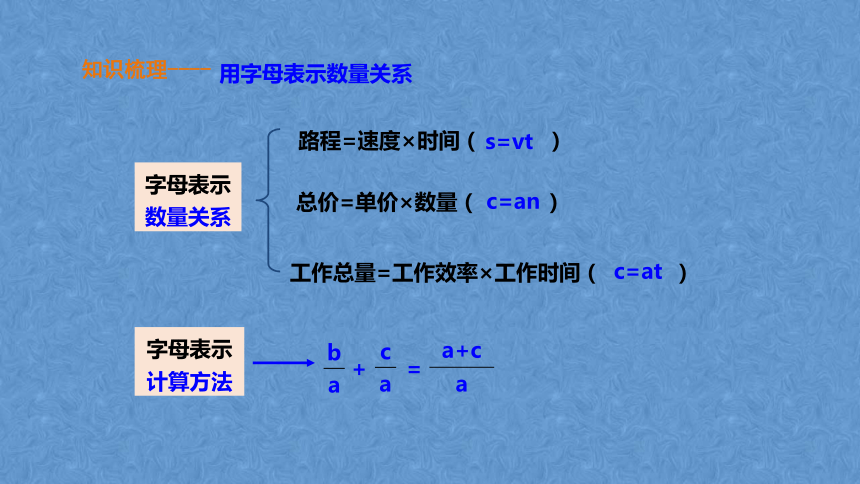
用字母表示数量关系
路程=速度×时间( )
s=vt
总价=单价×数量( )
c=an
字母表示 数量关系
字母表示计算方法
工作总量=工作效率×工作时间( )
c=at
b
a
+ =
c
a
a+c
a
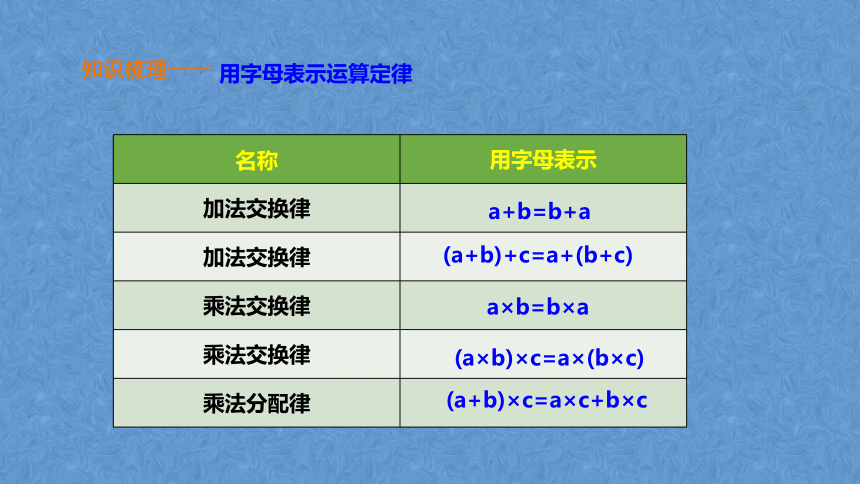
名称 用字母表示
加法交换律
加法交换律
乘法交换律
乘法交换律
乘法分配律
知识梳理----
用字母表示运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
知识梳理----
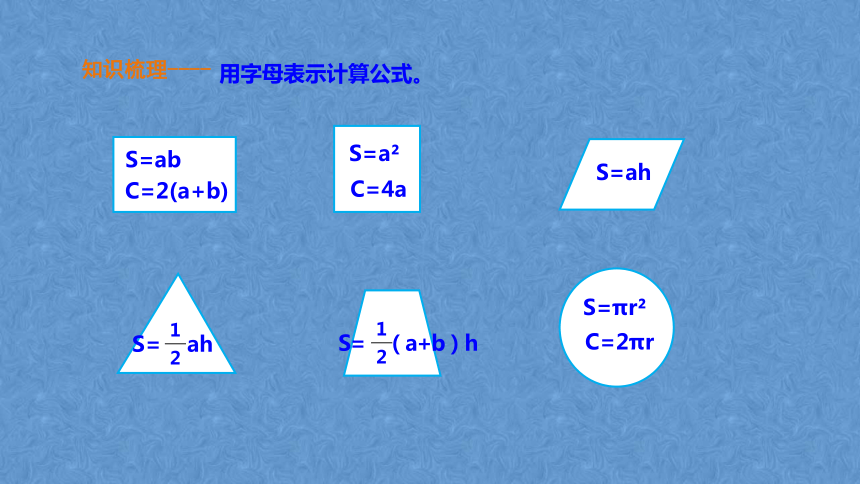
用字母表示计算公式。
S=ab
C=2(a+b)
S=a
C=4a
S=ah
S=πr
C=2πr
S= ah
1
2
S= (a+b)h
1
2
知识梳理----
用字母表示计算公式。
V=abh
V=a
V=πr h
V= πr h
1
3
V=Sh
S=2(ab+ah+bh)
S=6a
s=2πr +2πrh
1、小明每天上学时间为2小时,若他家到学校的路程为s千米,
则他上学的速度为( )千米。
2、某学校初三年级12个班,每班有团员a人,则初三年级共有
员人数为( )人。
3、买一副羽毛球拍儿需要m元,买一副乒乓球拍儿需要n元,买
6副羽毛球和8副羽毛球乒乓球拍儿共需( )元。
4、个长方形的,长是8米,宽是a米,则长方形的周长是
( )米。
典例训练
填 一 填
s÷2
12a
6m+8n
2(8+a)
等式
知识梳理----
等式与方程。
方程
方程的意义:
方程与等式的关系:
解方程:
含有未知数的等式叫作方程。
方程
求方程解的过程叫作解方程。
典例训练
5+x=16 ( ) 4a+5b ( )
20÷4=5 ( ) 4x+7=9 ( )
X+y>25-c ( ) 6+x ( )
判断下列哪些是方程(是的画√,不是的画×。)
×
×
√
√
×
×
典例训练
(1)一个排球x元。
240元
看图列方程
方程: 。
Y克
Y克
200克
300克
方程: 。
4x=240
2y+200=300
(2)
知识梳理----
解方程的依据→等式的性质
解下面的方程,并说一说你是怎么解的。
9x-1.8 = 5.4 0.8x+1.2x = 25
解:
9x-1.8+1.8 = 5.4+1.8
9x÷9 =7.2÷9
x=0.8
解:
2x= 25
2x÷2 = 25÷2
x=12.5
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立。
等式的性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
典例训练
解下面的方程。
2
7
x - x=
3
4
3
5
x=20×
1
4
解:
x=
5
7
3
4
x= ÷
3
4
5
7
x=
21
20
解:
x=5
x= 5÷
3
5
x=
25
3
3
5
典例训练
解下面的方程。
5
21
5x-3× =
5
7
25%+10x=
4
5
解:
5x- =
5
7
5
7
5x= +
5
7
5
7
x= ÷5
10
7
x=
2
7
解:
+10x=
4
5
10x= -
4
5
1
4
x= ÷10
11
20
x=
11
200
1
4
知识梳理----
用方程解决问题。
列方程解决下面的问题。
果品商店购进20 箱苹果,购进苹果的箱数是橘子箱数的 。商店购进了多少箱橘子?
4
5
橘子的箱数× =苹果的箱数
4
5
解:设商店购进了x箱橘子。
答:商店购进了25箱橘子。
x=25
x=20
x ÷ =20÷
4
5
4
5
4
5
妙想和乐乐一共收集了128 枚邮票。
妙想收集的邮票数是乐乐的3 倍。
知识梳理
妙想、乐乐各收集了多少枚邮票?
解:乐乐收集了x枚邮票,妙想收集了3x枚。
x+3x=128
x=32
32×3=96(张)
答:妙想收集了96枚邮票;
乐乐收集了32枚邮票。
知识梳理
淘气家和奇思家相距1240 m。一天,两人约定在两家之间的路上会合。淘气每分钟走75 m,奇思每分钟走80 m,两人同时从家出发,多长时间后能相遇?
解:设x分钟后两车能相遇。
(75+80)x=1240
x=8
答:8分钟后能相遇。
知识梳理----
用方程解决问题的步骤。
用方程解决问题的步骤
审题,理解题意;
1
找出等量关系;
2
根据等量关系列方程;
3
解方程;
4
检验写答语。
5
这一步很关键哦!
典例训练
甲、乙两地的公路长285千米,客、货两车分别从甲乙两地同时出发,相向而行,经过3小时两车相遇。已知客车每小时行45千米。货车每小时行驶多少千米?
解:设货车每小时行驶x千米。
答:货车每小时行驶50千米。
(x+45)×3=285
x+45=285÷3
x=50
典例训练
一次数学竞赛共有20道题。做对一道题得5分,做错一题倒扣3分,刘冬考了52分,你知道刘冬做对了几道题?
解:设刘冬做对了x道题,做错了(20-x)道题。
答:刘冬做对了14道题。
5x-3(20-x)=52
8x-60=52
x=14
课堂总结
你学会了那些知识?
我学会了……
复习了式与方程的知识。
式 与 方 程
数学北师大版 六年级下
知识导入
看到这些字母你能立刻想到什么?
CCTV
SOS
UFO
NBA
cm
知识梳理----
用字母表示规律
1、(1)淘气利用圆片摆出下面的图案。
1×1
2×2
3×3
4×4
……
第n 个图案用多少个圆片?请你用含有字母的式子表示。
n×n=n
用字母表示数可以概括地表示规律。
知识梳理----
用字母表示规律。
(2)生活中还有哪些规律能利用这个式子表示?
一个边长是 ncm的正方形,面积是 n cm 。
一个方阵,每排n 人, 有n排,共有n 人。
典例训练
按如下方式摆放餐桌和椅子,填表。
桌子张数 1 2 3 4 …… n
可坐人数
6
8
10
12
4+2n
知识梳理----
用字母表示数
用字母
表示数
用字母表示数量关系
用字母表示运算定律
用字母表示计算公式
用字母表示规律
说一说:可以用字母表示哪些数?
知识梳理----
用字母表示数量关系
路程=速度×时间( )
s=vt
总价=单价×数量( )
c=an
字母表示 数量关系
字母表示计算方法
工作总量=工作效率×工作时间( )
c=at
b
a
+ =
c
a
a+c
a
名称 用字母表示
加法交换律
加法交换律
乘法交换律
乘法交换律
乘法分配律
知识梳理----
用字母表示运算定律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
知识梳理----
用字母表示计算公式。
S=ab
C=2(a+b)
S=a
C=4a
S=ah
S=πr
C=2πr
S= ah
1
2
S= (a+b)h
1
2
知识梳理----
用字母表示计算公式。
V=abh
V=a
V=πr h
V= πr h
1
3
V=Sh
S=2(ab+ah+bh)
S=6a
s=2πr +2πrh
1、小明每天上学时间为2小时,若他家到学校的路程为s千米,
则他上学的速度为( )千米。
2、某学校初三年级12个班,每班有团员a人,则初三年级共有
员人数为( )人。
3、买一副羽毛球拍儿需要m元,买一副乒乓球拍儿需要n元,买
6副羽毛球和8副羽毛球乒乓球拍儿共需( )元。
4、个长方形的,长是8米,宽是a米,则长方形的周长是
( )米。
典例训练
填 一 填
s÷2
12a
6m+8n
2(8+a)
等式
知识梳理----
等式与方程。
方程
方程的意义:
方程与等式的关系:
解方程:
含有未知数的等式叫作方程。
方程
求方程解的过程叫作解方程。
典例训练
5+x=16 ( ) 4a+5b ( )
20÷4=5 ( ) 4x+7=9 ( )
X+y>25-c ( ) 6+x ( )
判断下列哪些是方程(是的画√,不是的画×。)
×
×
√
√
×
×
典例训练
(1)一个排球x元。
240元
看图列方程
方程: 。
Y克
Y克
200克
300克
方程: 。
4x=240
2y+200=300
(2)
知识梳理----
解方程的依据→等式的性质
解下面的方程,并说一说你是怎么解的。
9x-1.8 = 5.4 0.8x+1.2x = 25
解:
9x-1.8+1.8 = 5.4+1.8
9x÷9 =7.2÷9
x=0.8
解:
2x= 25
2x÷2 = 25÷2
x=12.5
等式的性质1:等式两边同时加上或减去同一个数,等式仍然成立。
等式的性质2:等式两边同时乘或除以同一个数(0除外),等式仍然成立。
典例训练
解下面的方程。
2
7
x - x=
3
4
3
5
x=20×
1
4
解:
x=
5
7
3
4
x= ÷
3
4
5
7
x=
21
20
解:
x=5
x= 5÷
3
5
x=
25
3
3
5
典例训练
解下面的方程。
5
21
5x-3× =
5
7
25%+10x=
4
5
解:
5x- =
5
7
5
7
5x= +
5
7
5
7
x= ÷5
10
7
x=
2
7
解:
+10x=
4
5
10x= -
4
5
1
4
x= ÷10
11
20
x=
11
200
1
4
知识梳理----
用方程解决问题。
列方程解决下面的问题。
果品商店购进20 箱苹果,购进苹果的箱数是橘子箱数的 。商店购进了多少箱橘子?
4
5
橘子的箱数× =苹果的箱数
4
5
解:设商店购进了x箱橘子。
答:商店购进了25箱橘子。
x=25
x=20
x ÷ =20÷
4
5
4
5
4
5
妙想和乐乐一共收集了128 枚邮票。
妙想收集的邮票数是乐乐的3 倍。
知识梳理
妙想、乐乐各收集了多少枚邮票?
解:乐乐收集了x枚邮票,妙想收集了3x枚。
x+3x=128
x=32
32×3=96(张)
答:妙想收集了96枚邮票;
乐乐收集了32枚邮票。
知识梳理
淘气家和奇思家相距1240 m。一天,两人约定在两家之间的路上会合。淘气每分钟走75 m,奇思每分钟走80 m,两人同时从家出发,多长时间后能相遇?
解:设x分钟后两车能相遇。
(75+80)x=1240
x=8
答:8分钟后能相遇。
知识梳理----
用方程解决问题的步骤。
用方程解决问题的步骤
审题,理解题意;
1
找出等量关系;
2
根据等量关系列方程;
3
解方程;
4
检验写答语。
5
这一步很关键哦!
典例训练
甲、乙两地的公路长285千米,客、货两车分别从甲乙两地同时出发,相向而行,经过3小时两车相遇。已知客车每小时行45千米。货车每小时行驶多少千米?
解:设货车每小时行驶x千米。
答:货车每小时行驶50千米。
(x+45)×3=285
x+45=285÷3
x=50
典例训练
一次数学竞赛共有20道题。做对一道题得5分,做错一题倒扣3分,刘冬考了52分,你知道刘冬做对了几道题?
解:设刘冬做对了x道题,做错了(20-x)道题。
答:刘冬做对了14道题。
5x-3(20-x)=52
8x-60=52
x=14
课堂总结
你学会了那些知识?
我学会了……
复习了式与方程的知识。
