6.4 章末复习提升课 第六章 计数原理 人教A版选择性必修第三册 课件(共38张PPT)
文档属性
| 名称 | 6.4 章末复习提升课 第六章 计数原理 人教A版选择性必修第三册 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览










文档简介
(共38张PPT)
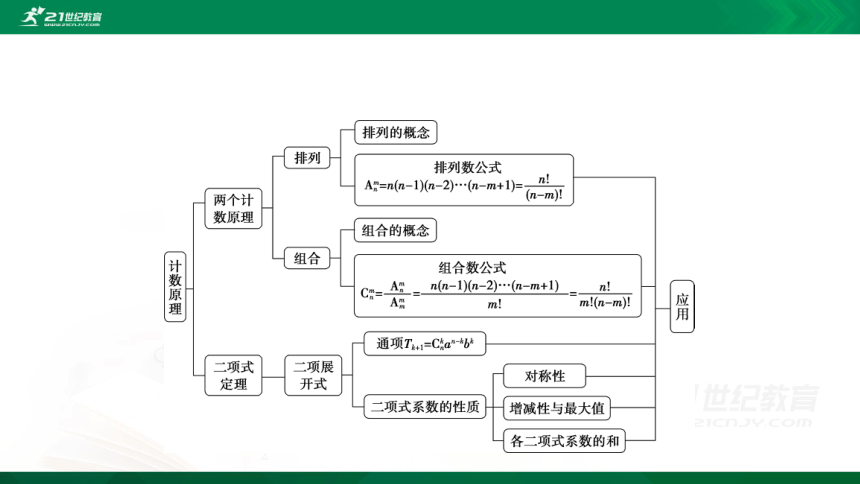
第六章 计数原理
章末复习提升课
素养一 数学抽象、逻辑推理
在本章中,利用两个计数原理和排列组合知识解决一些计数问题,可以培养学生的数学抽象、逻辑推理的核心素养.
主题1 计数原理的应用
(1)有红、黄、蓝旗各3面,每次升1面、2面或3面在旗杆上纵向排列表示不同的信号,顺序不同则表示不同的信号,共可以组成________种信号.
(2)(2021·西工大附中质检)回文数是指正读反读都一样的正整数,如22,343,1 221,94 249等.显然两位回文数有9个,即11,22,33,…,99;三位回文数有90个,即101,111,121,131,…,191,202,…,999.则四位回文数有________个;2n(n∈N*)位回文数有________个.
【解析】 (1)每次升1面旗可组成3种不同的信号,每次升2面旗可组成3×3=9(种)不同的信号,每次升3面旗可组成3×3×3=27(种)不同的信号.根据分类加法计数原理,共可组成3+9+27=39(种)不同的信号.
(2)由题意,可知四位回文数的特点为中间两位数是相同的,千位数和个位数相同但都不能为0,第一步,选千位数和个位数,共有9种选法;第二步,选中间两位数,共有10种选法.由分步乘法计数原理可得,四位回文数共有9×10=90(个).在2n(n∈N*)位回文数中.第一步,先选左边的第1个数,共有9种选法;第二步,选左边的第2个数,共有10种选法……第n步,选左边的第n个数,共有10种选法.由分步乘法计数原理可得,2n位回文数共有9×10n-1个.
【答案】 (1)39 (2)90 9×10n-1
使用两个计数原理应注意的问题
(1)对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
(2)当两个原理混合使用时,一般是先分类,在每类方法里再分步.
√
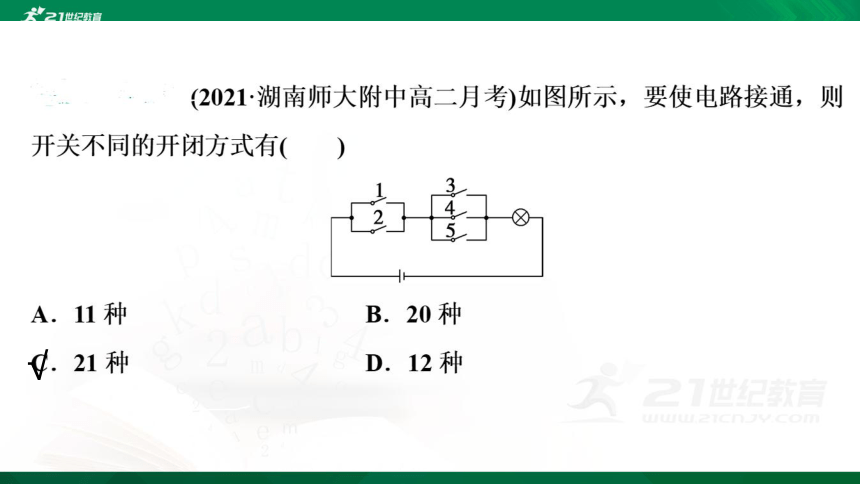
解析:根据题意,若电路接通,则开关1,2中至少有1个闭合,开关3,4,5中至少有1个闭合.对于开关1,2,开关不同的开闭方式共有2×2=4(种),其中全部断开的有1种情况,则至少有1个开关闭合的情况有4-1=3(种).对于开关3,4,5,开关不同的开闭方式共有2×2×2=8(种),其中全部断开的有1种情况,则至少有1个开关闭合的情况有8-1=7(种),故要使电路接通,开关不同的开闭方式共有3×7=21(种).故选C.
主题2 排列组合的综合应用
(1)(2021·嘉兴市高三期末)3男3女六位同学站成一排,则3位女生中有且只有两位女生相邻的不同排法种数是( )
A.576 B.432 C.388 D.216
(2)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
√
√
(1)排列组合的解题策略
①把握问题实质,确定是“分类”还是“分步”
②遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
(2)解决排列组合应用题的常用方法
①合理分类,准确分步;
②特殊优先,一般在后;
③先取后排,间接排除;
④集团捆绑,间隔插空;
⑤抽象问题,构造模型;
⑥均分除序,定序除序.
1.四面体的一个顶点为A,从其他顶点和各棱的中点中取3个点,使它们和点A在同一平面上,不同的取法有( )
A.30种 B.33种
C.36种 D.39种
√
2.从5名学生中选出4名分别参加A,B,C,D四科竞赛,其中甲不能参加C,D两科竞赛,则不同的参赛方案种数为________.
素养二 数学运算
二项式定理中求展开式的项,系数或二项式系数以及利用二项式定理求解整除系数问题等都体现了数学运算的核心素养.
√
二项式定理的问题类型及解题策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中满足一定条件的项的系数:先写出其通项公式,再由条件确定系数,然后代入通项公式求出此项的系数.
(4)确定二项展开式中的二项式系数或系数最大或最小的项:利用二项式系数的性质求解.
√
√
√
赋值法的应用
(1)解决的问题类型:与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和.
(2)应用技巧:通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
[注意] 求各项系数的绝对值的和时,要先根据绝对值里面数的符号赋值求解.
1.(2021·杭州市高三质检)已知(x2+1)(2x-1)7=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9(x∈R),则a1=( )
A.-30 B.30
C.-40 D.40
√
√
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第六章 计数原理
章末复习提升课
素养一 数学抽象、逻辑推理
在本章中,利用两个计数原理和排列组合知识解决一些计数问题,可以培养学生的数学抽象、逻辑推理的核心素养.
主题1 计数原理的应用
(1)有红、黄、蓝旗各3面,每次升1面、2面或3面在旗杆上纵向排列表示不同的信号,顺序不同则表示不同的信号,共可以组成________种信号.
(2)(2021·西工大附中质检)回文数是指正读反读都一样的正整数,如22,343,1 221,94 249等.显然两位回文数有9个,即11,22,33,…,99;三位回文数有90个,即101,111,121,131,…,191,202,…,999.则四位回文数有________个;2n(n∈N*)位回文数有________个.
【解析】 (1)每次升1面旗可组成3种不同的信号,每次升2面旗可组成3×3=9(种)不同的信号,每次升3面旗可组成3×3×3=27(种)不同的信号.根据分类加法计数原理,共可组成3+9+27=39(种)不同的信号.
(2)由题意,可知四位回文数的特点为中间两位数是相同的,千位数和个位数相同但都不能为0,第一步,选千位数和个位数,共有9种选法;第二步,选中间两位数,共有10种选法.由分步乘法计数原理可得,四位回文数共有9×10=90(个).在2n(n∈N*)位回文数中.第一步,先选左边的第1个数,共有9种选法;第二步,选左边的第2个数,共有10种选法……第n步,选左边的第n个数,共有10种选法.由分步乘法计数原理可得,2n位回文数共有9×10n-1个.
【答案】 (1)39 (2)90 9×10n-1
使用两个计数原理应注意的问题
(1)对于一些比较复杂的既要运用分类加法计数原理又要运用分步乘法计数原理的问题,我们可以恰当地画出示意图或列出表格,使问题更加直观、清晰.
(2)当两个原理混合使用时,一般是先分类,在每类方法里再分步.
√
解析:根据题意,若电路接通,则开关1,2中至少有1个闭合,开关3,4,5中至少有1个闭合.对于开关1,2,开关不同的开闭方式共有2×2=4(种),其中全部断开的有1种情况,则至少有1个开关闭合的情况有4-1=3(种).对于开关3,4,5,开关不同的开闭方式共有2×2×2=8(种),其中全部断开的有1种情况,则至少有1个开关闭合的情况有8-1=7(种),故要使电路接通,开关不同的开闭方式共有3×7=21(种).故选C.
主题2 排列组合的综合应用
(1)(2021·嘉兴市高三期末)3男3女六位同学站成一排,则3位女生中有且只有两位女生相邻的不同排法种数是( )
A.576 B.432 C.388 D.216
(2)安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )
A.12种 B.18种 C.24种 D.36种
√
√
(1)排列组合的解题策略
①把握问题实质,确定是“分类”还是“分步”
②遵循两个原则:一是按元素的性质进行分类;二是按事情发生的过程进行分步.
(2)解决排列组合应用题的常用方法
①合理分类,准确分步;
②特殊优先,一般在后;
③先取后排,间接排除;
④集团捆绑,间隔插空;
⑤抽象问题,构造模型;
⑥均分除序,定序除序.
1.四面体的一个顶点为A,从其他顶点和各棱的中点中取3个点,使它们和点A在同一平面上,不同的取法有( )
A.30种 B.33种
C.36种 D.39种
√
2.从5名学生中选出4名分别参加A,B,C,D四科竞赛,其中甲不能参加C,D两科竞赛,则不同的参赛方案种数为________.
素养二 数学运算
二项式定理中求展开式的项,系数或二项式系数以及利用二项式定理求解整除系数问题等都体现了数学运算的核心素养.
√
二项式定理的问题类型及解题策略
(1)确定二项式中的有关元素:一般是根据已知条件,列出等式,从而可解得所要求的二项式中的有关元素.
(2)确定二项展开式中的常数项:先写出其通项公式,令未知数的指数为零,从而确定项数,然后代入通项公式,即可确定常数项.
(3)求二项展开式中满足一定条件的项的系数:先写出其通项公式,再由条件确定系数,然后代入通项公式求出此项的系数.
(4)确定二项展开式中的二项式系数或系数最大或最小的项:利用二项式系数的性质求解.
√
√
√
赋值法的应用
(1)解决的问题类型:与二项式系数有关,包括求展开式中二项式系数最大的项、各项的二项式系数或系数的和、奇数项或者偶数项的二项式系数或系数的和以及各项系数的绝对值的和.
(2)应用技巧:通过观察展开式右边的结构特点和所求式子的关系,确定给字母所赋的值,有时赋值后得到的式子比所求式子多一项或少一项,此时要专门求出这一项,而在求奇数项或者偶数项的二项式系数或系数的和时,往往要两次赋值,再由方程组求出结果.
[注意] 求各项系数的绝对值的和时,要先根据绝对值里面数的符号赋值求解.
1.(2021·杭州市高三质检)已知(x2+1)(2x-1)7=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9(x∈R),则a1=( )
A.-30 B.30
C.-40 D.40
√
√
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
