2021-2022学年六年级下学期数学+总复习第十二课时+图形与测量+(课件)(共22页)
文档属性
| 名称 | 2021-2022学年六年级下学期数学+总复习第十二课时+图形与测量+(课件)(共22页) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 16:05:59 | ||
图片预览



文档简介
(共22张PPT)
图形与测量
数学北师大版 六年级下
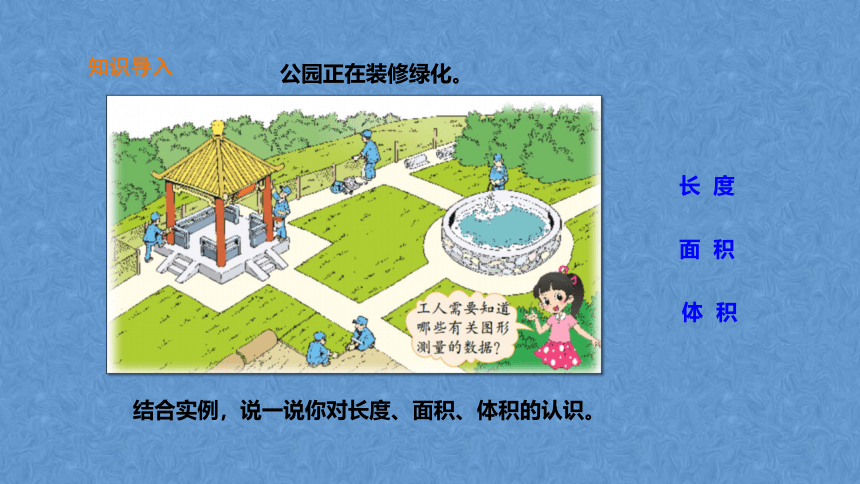
知识导入
公园正在装修绿化。
面 积
长 度
体 积
结合实例,说一说你对长度、面积、体积的认识。
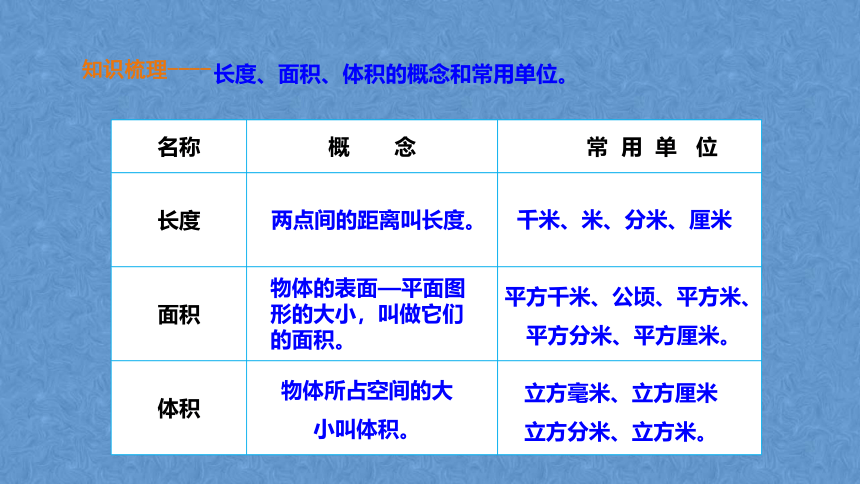
知识梳理----
长度、面积、体积的概念和常用单位。
名称 概 念 常 用 单 位
长度
面积
体积
两点间的距离叫长度。
千米、米、分米、厘米
物体的表面—平面图形的大小,叫做它们的面积。
平方千米、公顷、平方米、平方分米、平方厘米。
物体所占空间的大小叫体积。
立方毫米、立方厘米 立方分米、立方米。
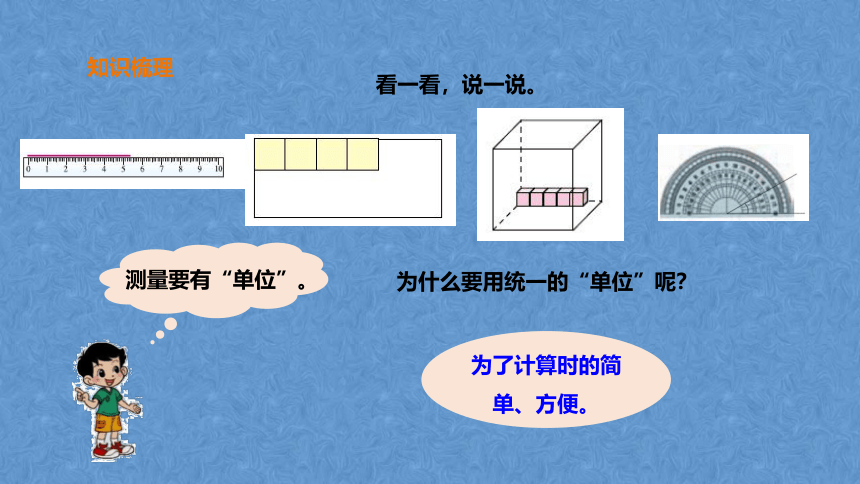
知识梳理
看一看,说一说。
为什么要用统一的“单位”呢?
为了计算时的简单、方便。
测量要有“单位”。
知识梳理----
单位间的进率。
名称 单位间的进率
长度
面积
体积
1km=( )m 1m =( )dm
1dm=( )cm 1cm =( )mm
1000
10
10
10
1km =( )公顷 1公顷=( )m
1m =( )dm 1dm =( )cm
1cm =( )mm
100
10000
100
100
100
1m =( )dm 1dm =( )cm
1cm =( )mm 1L =( )mL
1000
1000
1000
1000
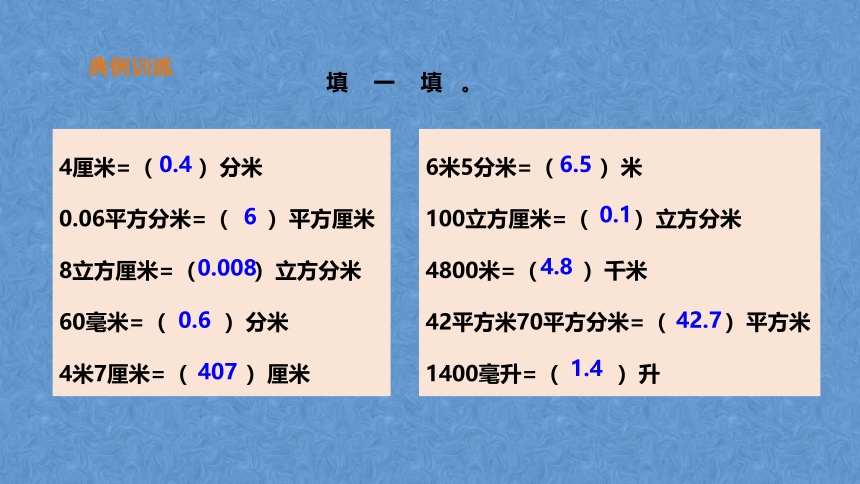
典例训练
填 一 填 。
4厘米=( )分米
0.06平方分米=( )平方厘米
8立方厘米=( )立方分米
60毫米=( )分米
4米7厘米=( )厘米
6米5分米=( )米
100立方厘米=( )立方分米
4800米=( )千米
42平方米70平方分米=( )平方米
1400毫升=( )升
0.4
6
0.008
0.6
407
6.5
0.1
4.8
42.7
1.4
知识梳理
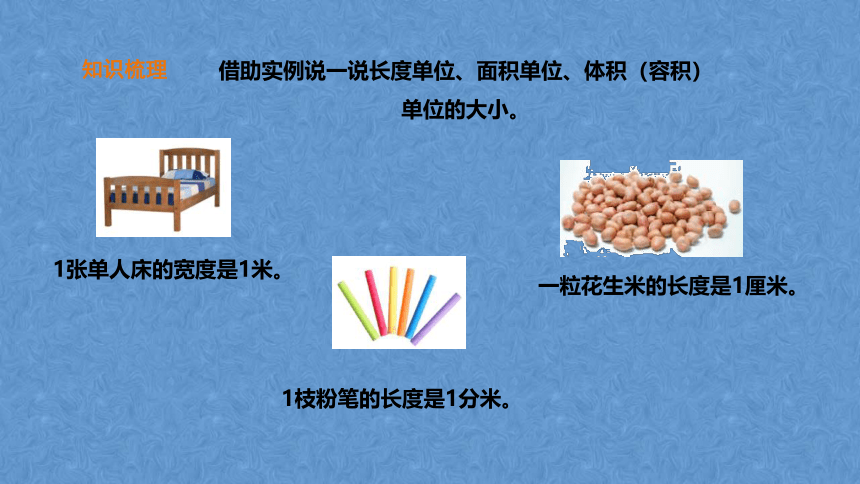
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1张单人床的宽度是1米。
1枝粉笔的长度是1分米。
一粒花生米的长度是1厘米。
知识梳理
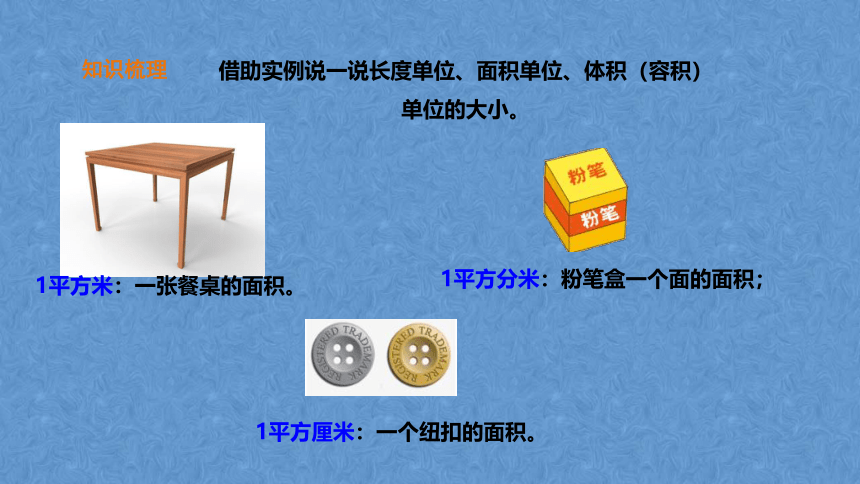
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1平方米:一张餐桌的面积。
1平方分米:粉笔盒一个面的面积;
1平方厘米:一个纽扣的面积。
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1立方米:一个洗衣机的体积。
一瓶眼药水大约5毫升。
1L:两瓶矿缺水的体积。
典例训练
填上适当的单位名称。
1、公园的面积4( )。
2、马拉松长跑是国际上普及长跑比赛项目,赛程是42.195( )。
3、一瓶矿泉水的体积是550( )。
4、一个冰箱的容积是( )。
5、教室内黑板的长度是3( )。
6、成人手掌的面积是1( )。
公顷
千米
毫升
升
米
平方分米
知识梳理
想办法求出下面图形的周长,并说说什么是周长。
量出每边的长度,再加起来。
用线量出周长,再量出线的长度。
周长:围成图形一周的长度叫做这个图形的周长。
知识梳理
我们学过的图形的周长公式。
C=2(a+b)
a
C=4a
.
r
d=2r
o
公式:C=πd→d=C÷π
C=2πR→r=C÷2π
a
b
知识梳理
分别说出已学过的多边形的面积计算公式,并说说公式之间的联系。
S=ab
a
b
a
S=a
a
b
h
S=ah
a
b
h
S= ah
1
2
h
a
b
S= (a+b)
1
2
知识梳理
想一想圆的面积计算公式的探索过程,并说一说圆的面积公式。
a
b
= πr
r
因为长方形的面积=( )× ( ),
所以圆的面积=( )×( )=( )。
a
b
r
πr2
C
2
典例训练
计算下面图形的面积和周长。(单位:cm)
5
8
6
C=2×(8+5)
=26(cm)
S=8×5
=40(cm )
8
6
10
C=4×6
=24(cm)
S=6×6
=36(cm )
C=10+8+6
=24(cm)
S=5×8÷2
=20(cm )
5
典例训练
计算下面图形的面积和周长。(单位:cm)
9
6
5
7
12
8
6
C=2×(6+9)
=30(cm)
S=9×5
=45(cm )
C=2×8+7+12
=35(cm)
S=(12+7)×6÷2
=57(cm )
典例训练
求下面图形的周长和面积。
.
r=2cm
o
d=8cm
C=2πr
=2×3.14×2
=12.56(cm)
S=πr
=3.14×2
=12.56(cm )
C=3.14×8÷2+8
=20.56(cm)
C=3.14×(8÷2) ÷2
=25.12(cm )
知识梳理
举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
表面积的概念:一个立体图形所有的面的面积总和,
叫做它们的表面积。
体积的概念: 一个立体图形所占空间的大小,叫做
它的体积。
V= Sh
名 称 图 形 表面积公式 体积公式 长方体
正方体 圆 柱 圆 锥 --------
知识梳理
填 一 填
a
b
h
a
h
r
r
h
S=2(ab+ah+bh)
S=6a
S=2πr +2πrh
V=abh
V=a
V=πr h
V= πr h
1
3
1
3
V=Sh
典例训练
判 断 。
( )圆柱说:我的体积是圆锥的3倍。
( )长方体说:我和一个圆柱等底等高,我俩的体积相等。
( )长方体说:把我改铸成一个圆锥,我的体积不变。
( )油桶说:我能盛多少水,我的体积就是多少。
( )正方体说:我的棱长是6分米,我的表面积和体积相等。
( )同一个物体的体积比容积大。
×
√
√
×
×
√
典例训练
把一个长8厘米、宽4厘米、高6厘米的长方体木块,切成一个最大的圆柱,圆柱的体积是多少立方厘米?
(1)以6厘米为底面直径,
4厘米为高;
3.14×( ) ×4
=3.14×9×4
=113.04(立方厘米)
6
2
(2)以4厘米为底面直径,
6厘米为高;
3.14×( ) ×6
=3.14×4×6
=75.36(立方厘米)
(2)以4厘米为底面直径,
8厘米为高;
3.14×( ) ×8
=3.14×4×8
=100.48(立方厘米)
4
2
4
2
答:圆柱的体积是113.04立方厘米。
课堂总结
你学会了那些知识?
我学会了……
2、复面图形的周长和面积。
3、复习了立体图形的表面积和体积。
1、复习了长度、面积、体积的单位。
图形与测量
数学北师大版 六年级下
知识导入
公园正在装修绿化。
面 积
长 度
体 积
结合实例,说一说你对长度、面积、体积的认识。
知识梳理----
长度、面积、体积的概念和常用单位。
名称 概 念 常 用 单 位
长度
面积
体积
两点间的距离叫长度。
千米、米、分米、厘米
物体的表面—平面图形的大小,叫做它们的面积。
平方千米、公顷、平方米、平方分米、平方厘米。
物体所占空间的大小叫体积。
立方毫米、立方厘米 立方分米、立方米。
知识梳理
看一看,说一说。
为什么要用统一的“单位”呢?
为了计算时的简单、方便。
测量要有“单位”。
知识梳理----
单位间的进率。
名称 单位间的进率
长度
面积
体积
1km=( )m 1m =( )dm
1dm=( )cm 1cm =( )mm
1000
10
10
10
1km =( )公顷 1公顷=( )m
1m =( )dm 1dm =( )cm
1cm =( )mm
100
10000
100
100
100
1m =( )dm 1dm =( )cm
1cm =( )mm 1L =( )mL
1000
1000
1000
1000
典例训练
填 一 填 。
4厘米=( )分米
0.06平方分米=( )平方厘米
8立方厘米=( )立方分米
60毫米=( )分米
4米7厘米=( )厘米
6米5分米=( )米
100立方厘米=( )立方分米
4800米=( )千米
42平方米70平方分米=( )平方米
1400毫升=( )升
0.4
6
0.008
0.6
407
6.5
0.1
4.8
42.7
1.4
知识梳理
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1张单人床的宽度是1米。
1枝粉笔的长度是1分米。
一粒花生米的长度是1厘米。
知识梳理
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1平方米:一张餐桌的面积。
1平方分米:粉笔盒一个面的面积;
1平方厘米:一个纽扣的面积。
借助实例说一说长度单位、面积单位、体积(容积)单位的大小。
1立方米:一个洗衣机的体积。
一瓶眼药水大约5毫升。
1L:两瓶矿缺水的体积。
典例训练
填上适当的单位名称。
1、公园的面积4( )。
2、马拉松长跑是国际上普及长跑比赛项目,赛程是42.195( )。
3、一瓶矿泉水的体积是550( )。
4、一个冰箱的容积是( )。
5、教室内黑板的长度是3( )。
6、成人手掌的面积是1( )。
公顷
千米
毫升
升
米
平方分米
知识梳理
想办法求出下面图形的周长,并说说什么是周长。
量出每边的长度,再加起来。
用线量出周长,再量出线的长度。
周长:围成图形一周的长度叫做这个图形的周长。
知识梳理
我们学过的图形的周长公式。
C=2(a+b)
a
C=4a
.
r
d=2r
o
公式:C=πd→d=C÷π
C=2πR→r=C÷2π
a
b
知识梳理
分别说出已学过的多边形的面积计算公式,并说说公式之间的联系。
S=ab
a
b
a
S=a
a
b
h
S=ah
a
b
h
S= ah
1
2
h
a
b
S= (a+b)
1
2
知识梳理
想一想圆的面积计算公式的探索过程,并说一说圆的面积公式。
a
b
= πr
r
因为长方形的面积=( )× ( ),
所以圆的面积=( )×( )=( )。
a
b
r
πr2
C
2
典例训练
计算下面图形的面积和周长。(单位:cm)
5
8
6
C=2×(8+5)
=26(cm)
S=8×5
=40(cm )
8
6
10
C=4×6
=24(cm)
S=6×6
=36(cm )
C=10+8+6
=24(cm)
S=5×8÷2
=20(cm )
5
典例训练
计算下面图形的面积和周长。(单位:cm)
9
6
5
7
12
8
6
C=2×(6+9)
=30(cm)
S=9×5
=45(cm )
C=2×8+7+12
=35(cm)
S=(12+7)×6÷2
=57(cm )
典例训练
求下面图形的周长和面积。
.
r=2cm
o
d=8cm
C=2πr
=2×3.14×2
=12.56(cm)
S=πr
=3.14×2
=12.56(cm )
C=3.14×8÷2+8
=20.56(cm)
C=3.14×(8÷2) ÷2
=25.12(cm )
知识梳理
举例说明什么是立体图形的表面积。说一说长方体、正方体、圆柱的表面积的计算方法。
表面积的概念:一个立体图形所有的面的面积总和,
叫做它们的表面积。
体积的概念: 一个立体图形所占空间的大小,叫做
它的体积。
V= Sh
名 称 图 形 表面积公式 体积公式 长方体
正方体 圆 柱 圆 锥 --------
知识梳理
填 一 填
a
b
h
a
h
r
r
h
S=2(ab+ah+bh)
S=6a
S=2πr +2πrh
V=abh
V=a
V=πr h
V= πr h
1
3
1
3
V=Sh
典例训练
判 断 。
( )圆柱说:我的体积是圆锥的3倍。
( )长方体说:我和一个圆柱等底等高,我俩的体积相等。
( )长方体说:把我改铸成一个圆锥,我的体积不变。
( )油桶说:我能盛多少水,我的体积就是多少。
( )正方体说:我的棱长是6分米,我的表面积和体积相等。
( )同一个物体的体积比容积大。
×
√
√
×
×
√
典例训练
把一个长8厘米、宽4厘米、高6厘米的长方体木块,切成一个最大的圆柱,圆柱的体积是多少立方厘米?
(1)以6厘米为底面直径,
4厘米为高;
3.14×( ) ×4
=3.14×9×4
=113.04(立方厘米)
6
2
(2)以4厘米为底面直径,
6厘米为高;
3.14×( ) ×6
=3.14×4×6
=75.36(立方厘米)
(2)以4厘米为底面直径,
8厘米为高;
3.14×( ) ×8
=3.14×4×8
=100.48(立方厘米)
4
2
4
2
答:圆柱的体积是113.04立方厘米。
课堂总结
你学会了那些知识?
我学会了……
2、复面图形的周长和面积。
3、复习了立体图形的表面积和体积。
1、复习了长度、面积、体积的单位。
