3.5 平行线的性质定理 导学案(含答案)
文档属性
| 名称 | 3.5 平行线的性质定理 导学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 207.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-08 14:43:59 | ||
图片预览

文档简介
3.5 平行线的性质定理 导学案
【学习目标】
1.进一步熟悉证明的基本步骤和书写格式
2.会根据“两直线平行,同位角相等”证明平行线的其它性质定理
3.正确区别平行线的判定和性质.
【学习重点】平行线的性质定理的应用.
【学习过程】
一、课前准备
1.平行线有哪些性质?你能证明它们的正确性吗?
2.平行线的性质公理.
【预习检测】
1. 如图a∥b,写出相等的同位角: .
写出相等的内错角 ,
写出互补的同旁内角
2. 如图a∥b,∠1=68°,那么:∠2的度数为
3.如图,已知:DE∥BC,∠ABC=52°,∠BED=18°
求:∠ABE的度数
二、课堂学习
【自主探究,同伴交流】
自学课本87—88页内容后,小组内合作交流,讨论以下问题;
1. 已知:a∥b
求证:∠1=∠2
你证明的命题用文字叙述为
可以简单地叙述为
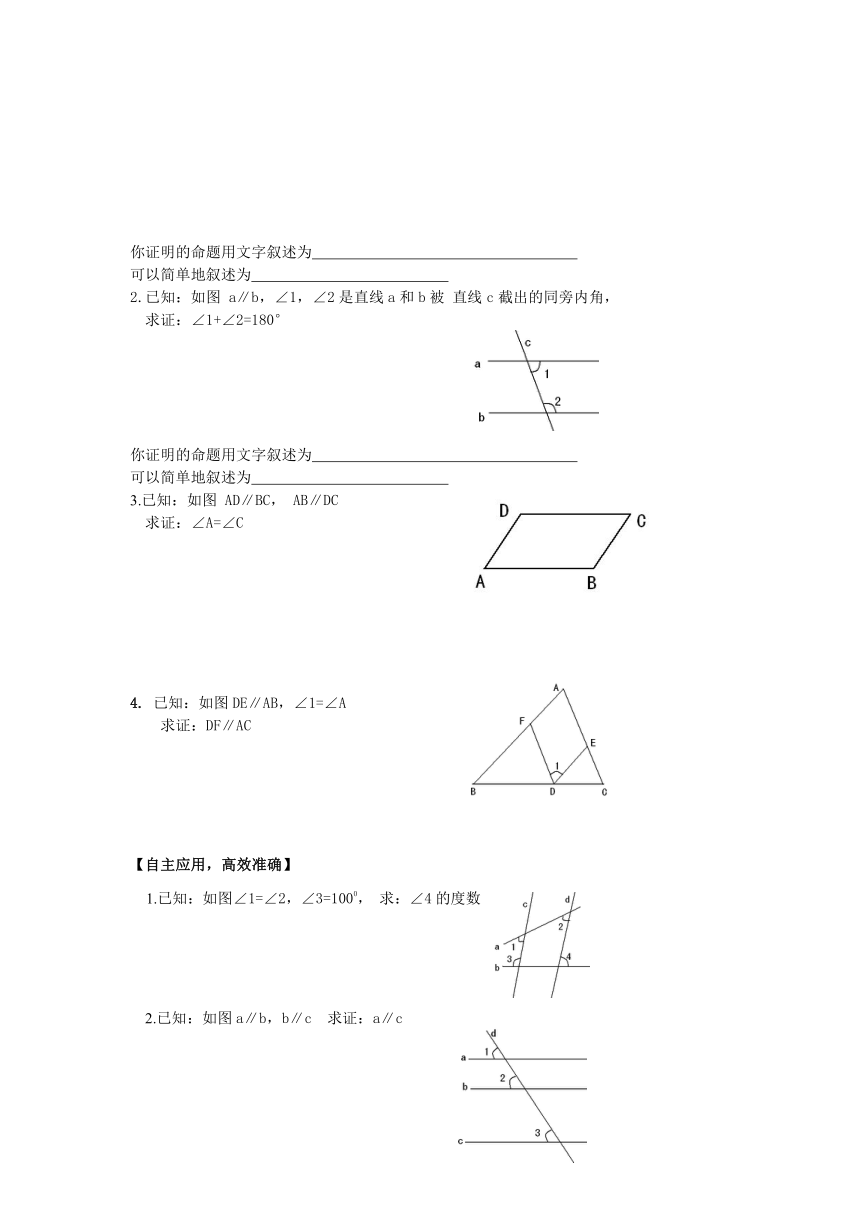
2.已知:如图 a∥b,∠1,∠2是直线a和b被 直线c截出的同旁内角,
求证:∠1+∠2=180°
你证明的命题用文字叙述为
可以简单地叙述为
3.已知:如图 AD∥BC, AB∥DC
求证:∠A=∠C
4. 已知:如图DE∥AB,∠1=∠A
求证:DF∥AC
【自主应用,高效准确】
1.已知:如图∠1=∠2,∠3=1000, 求:∠4的度数
2.已知:如图a∥b,b∥c 求证:a∥c
你证明的命题用文字叙述为
可以简单地叙述为
3. 已知:如图∠1=∠2=∠3=550, 求:∠4的度数
【拓展延伸,提升能力】
4、已知:如图AB∥CD求证:∠A+∠C+∠E=1800
5.已知:如图AB∥CD,猜想∠A、∠C、∠E的关系,并证明你的猜想.
6.已知:如图AB∥CD,∠B=1000,∠C= 1200,,, 求 ∠E的度数
【当堂巩固,达标测评】
1.如图所示AB∥CD,∠C=1150,∠A= 250,则∠E的度数为( )
A.700 B.800 C.900 D.1000
2. .如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )
A.750 B.650 C.550 D.500
3.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则∠BCD=
4. 如图已知AB∥CD∥EF,EG∥BD则图中和∠1相等的角有
5.潜望镜的两个镜面是平行放置的,光线经过平面镜的两次反射后互相平行,请运用学过的数学知识进行解释其中的原理.
【课堂小结,作业布置】:
【课后反思】
参考答案
3.5 平行线的性质定理
一、课前准备
【预习检测】
1同位角:∠4=∠2 ∠5=∠8 ∠3=∠6 ∠1=∠7
内错角:∠1=∠2 ∠5=∠6 同旁内角:∠2与∠5互补 ∠6与∠1互补
2、68°
3、解:∵DE∥BC ∠BED=18°
∴∠CBE=∠BED=18°(两直线平行内错角相等)
∵∠ABC=52°
∴∠ABE=∠ABC-∠CBE=34°
二、课堂学习
【自主探究,同伴交流】
证明:∵a∥b ∴∠2=∠3(两直线平行同位角相等)
∵∠1=∠3(对顶角相等)
∴∠1=∠2(等量代换)
证明的命题用文字叙述为:两条平行线被第三条直线所截,内错角相等
可以简单地叙述为:两直线平行内错角相等
证明:∵a∥b,∴∠2=∠3(两直线平行同位角相等)
∵∠1+∠3=180°(1平角=180°)
∴∠1+∠2=180°(等量代换)
证明的命题用文字叙述为:两条平行线被第三条直线所截,同旁内角互补
可以简单地叙述为:两直线平行同旁内角互补
证明:∵AD∥BC, AB∥DC
∴∠A+∠B=180°∠C+∠B=180°(两直线平行同旁内角互补)
∴∠A=180-∠B ∠C =180-∠B(等式的性质)
∴∠A=∠C(等式的性质)
证明:∵DE∥AB
∴∠A+∠AED=180°(两直线平行同旁内角互补)
∵∠1=∠A (已知)
∴∠1+∠AED=180°(等量代换)
∴DF∥AC(同旁内角互补两直线平行)
【自主应用,高效准确】
1、∠4 =80°
2、证明:∵a∥b,b∥c
∴∠1=∠2 ∠2 =∠3(两直线平行同位角相等)
∴∠1 =∠3(等量代换)
∴a∥c(同位角相等两直线平行)
证明的命题用文字叙述为:如果两条直线都与第三条直线互相平行,那么这两条直线互相平行
可以简单地叙述位:平行于同一条直线的两直线平行
3、∠4 =125°
【拓展延伸,提升能力】
4、提示:过E做EF∥AB或连接AC
5、∠A+∠C=∠E 证明:略
6、∠E =40°
【当堂巩固,达标测评】
1、C 2、B 3、25° 4、5个 5、略
【学习目标】
1.进一步熟悉证明的基本步骤和书写格式
2.会根据“两直线平行,同位角相等”证明平行线的其它性质定理
3.正确区别平行线的判定和性质.
【学习重点】平行线的性质定理的应用.
【学习过程】
一、课前准备
1.平行线有哪些性质?你能证明它们的正确性吗?
2.平行线的性质公理.
【预习检测】
1. 如图a∥b,写出相等的同位角: .
写出相等的内错角 ,
写出互补的同旁内角
2. 如图a∥b,∠1=68°,那么:∠2的度数为
3.如图,已知:DE∥BC,∠ABC=52°,∠BED=18°
求:∠ABE的度数
二、课堂学习
【自主探究,同伴交流】
自学课本87—88页内容后,小组内合作交流,讨论以下问题;
1. 已知:a∥b
求证:∠1=∠2
你证明的命题用文字叙述为
可以简单地叙述为
2.已知:如图 a∥b,∠1,∠2是直线a和b被 直线c截出的同旁内角,
求证:∠1+∠2=180°
你证明的命题用文字叙述为
可以简单地叙述为
3.已知:如图 AD∥BC, AB∥DC
求证:∠A=∠C
4. 已知:如图DE∥AB,∠1=∠A
求证:DF∥AC
【自主应用,高效准确】
1.已知:如图∠1=∠2,∠3=1000, 求:∠4的度数
2.已知:如图a∥b,b∥c 求证:a∥c
你证明的命题用文字叙述为
可以简单地叙述为
3. 已知:如图∠1=∠2=∠3=550, 求:∠4的度数
【拓展延伸,提升能力】
4、已知:如图AB∥CD求证:∠A+∠C+∠E=1800
5.已知:如图AB∥CD,猜想∠A、∠C、∠E的关系,并证明你的猜想.
6.已知:如图AB∥CD,∠B=1000,∠C= 1200,,, 求 ∠E的度数
【当堂巩固,达标测评】
1.如图所示AB∥CD,∠C=1150,∠A= 250,则∠E的度数为( )
A.700 B.800 C.900 D.1000
2. .如图所示a∥b,∠1=1050,∠2=1400 则∠3的度数为( )
A.750 B.650 C.550 D.500
3.如图所示AB∥CD,AC⊥BC,∠BAC=650, 则∠BCD=
4. 如图已知AB∥CD∥EF,EG∥BD则图中和∠1相等的角有
5.潜望镜的两个镜面是平行放置的,光线经过平面镜的两次反射后互相平行,请运用学过的数学知识进行解释其中的原理.
【课堂小结,作业布置】:
【课后反思】
参考答案
3.5 平行线的性质定理
一、课前准备
【预习检测】
1同位角:∠4=∠2 ∠5=∠8 ∠3=∠6 ∠1=∠7
内错角:∠1=∠2 ∠5=∠6 同旁内角:∠2与∠5互补 ∠6与∠1互补
2、68°
3、解:∵DE∥BC ∠BED=18°
∴∠CBE=∠BED=18°(两直线平行内错角相等)
∵∠ABC=52°
∴∠ABE=∠ABC-∠CBE=34°
二、课堂学习
【自主探究,同伴交流】
证明:∵a∥b ∴∠2=∠3(两直线平行同位角相等)
∵∠1=∠3(对顶角相等)
∴∠1=∠2(等量代换)
证明的命题用文字叙述为:两条平行线被第三条直线所截,内错角相等
可以简单地叙述为:两直线平行内错角相等
证明:∵a∥b,∴∠2=∠3(两直线平行同位角相等)
∵∠1+∠3=180°(1平角=180°)
∴∠1+∠2=180°(等量代换)
证明的命题用文字叙述为:两条平行线被第三条直线所截,同旁内角互补
可以简单地叙述为:两直线平行同旁内角互补
证明:∵AD∥BC, AB∥DC
∴∠A+∠B=180°∠C+∠B=180°(两直线平行同旁内角互补)
∴∠A=180-∠B ∠C =180-∠B(等式的性质)
∴∠A=∠C(等式的性质)
证明:∵DE∥AB
∴∠A+∠AED=180°(两直线平行同旁内角互补)
∵∠1=∠A (已知)
∴∠1+∠AED=180°(等量代换)
∴DF∥AC(同旁内角互补两直线平行)
【自主应用,高效准确】
1、∠4 =80°
2、证明:∵a∥b,b∥c
∴∠1=∠2 ∠2 =∠3(两直线平行同位角相等)
∴∠1 =∠3(等量代换)
∴a∥c(同位角相等两直线平行)
证明的命题用文字叙述为:如果两条直线都与第三条直线互相平行,那么这两条直线互相平行
可以简单地叙述位:平行于同一条直线的两直线平行
3、∠4 =125°
【拓展延伸,提升能力】
4、提示:过E做EF∥AB或连接AC
5、∠A+∠C=∠E 证明:略
6、∠E =40°
【当堂巩固,达标测评】
1、C 2、B 3、25° 4、5个 5、略
