3.4 平行线的判定定理 导学案(含答案)
文档属性
| 名称 | 3.4 平行线的判定定理 导学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 166.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-08 14:43:59 | ||
图片预览

文档简介
3.4 平行线的判定定理
学习目标:
1.初步了解证明的基本步骤和书写格式.
2.会根据“同位角相等,两直线平行”证明平行线的其它判定定理,并能简单应用这些结论.
3.感受几何中推理的严谨性、结论的确定性,发展演绎推理的能力.
学习重点:平行线的判定定理的应用.
学习过程
一、复习检测:
1、公理的定义、定理的定义
2.平行线的判定公理.
3、平行线的识别方法有:(1) .
(2) ,(3)
4、如果两条直线都和第三条直线平行,那么这两条直线
5.如图,请你填写一个条件,使得DE∥BC
你填写的条件是
二、自主学习,小组交流:
自学课本84—85页内容后,小组内合作交流,讨论以下问题;
1.说一说怎样用三角板画平行线,根据是什么?与同伴交流.
2.已知:如图 ∠1,∠2是直线a和b被 直线c截出的同旁内角,
且∠1+∠2=180°
求证:a∥b
你证明的命题用文字叙述为
可以简单地叙述为
几何语言
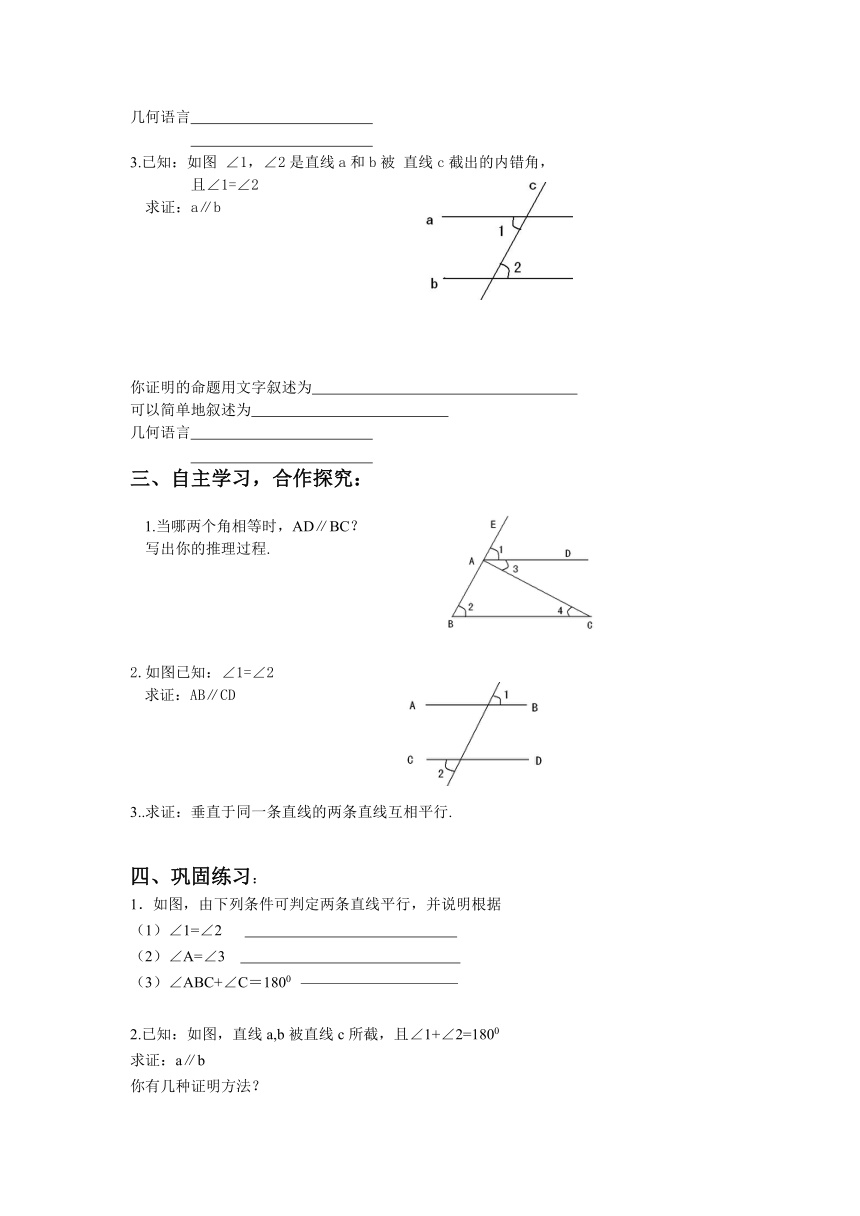
3.已知:如图 ∠1,∠2是直线a和b被 直线c截出的内错角,
且∠1=∠2
求证:a∥b
你证明的命题用文字叙述为
可以简单地叙述为
几何语言
三、自主学习,合作探究:
1.当哪两个角相等时,AD∥BC?
写出你的推理过程.
2.如图已知:∠1=∠2
求证:AB∥CD
3..求证:垂直于同一条直线的两条直线互相平行.
四、巩固练习:
1.如图,由下列条件可判定两条直线平行,并说明根据
(1)∠1=∠2
(2)∠A=∠3
(3)∠ABC+∠C=1800
2.已知:如图,直线a,b被直线c所截,且∠1+∠2=1800
求证:a∥b
你有几种证明方法?
3.已知;如图,BP交CD与点P,∠ABP+∠BPC=1800,∠1=∠2
求证:EB∥PF
五、拓展延伸:
1、已知:如图∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
2. 如图:AB∥CD,∠1=1000,∠2=1200
求∠α的度数。
六、我的收获:(包括知识点、解题方法和技巧等方面)
七、达标检测:
1.下列命题中,假命题是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角相等,两直线平行 D.同旁内角互补,两直线平行
2. 如图所示,下列条件中能判断直线AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠2=1800, D.∠3+∠4=900,
3.下列推理判断错误的是( )
A.∵∠1=∠2 ∴ a∥b, B.∵∠3+∠4=1800,∴ c∥d
C. ∵∠3=∠4 ∴ c∥d D.∵∠3+∠6=1800,∴ a∥b
4.填空:
(1)∵∠E=∠F ∴ ∥ ,( )
(2)∵∠A=∠FBC ∴ ∥ ,( )
(3)∵∠ +∠ =1800,∴ AB∥CD( )
5.光线经过玻璃砖发生折射,从玻璃砖出来的光线同样回发生折射, 如图,已知,∠1=∠4, ∠2=∠3
求证: c∥d
八、学(教)后反思:
参考答案
3.4 平行线的判定定理
一、课前准备
【预习检测】
1、(1)同位角相等两直线平行(2)内错角相等两直线平行(3)同旁内角互补两直线平行。2、互相平行。 3、∠ADE=∠ABC(答案不唯一)
二、课堂学习
【自主探究,同伴交流】
1略。2 、∵∠1+∠2=1800(已知)∠1+∠3=1800(1平角=1800)
∴∠2=∠3(等角的补角相等)
∴a∥b(同位角相等两直线平行)
两条直线被第三条直线截,如果同旁内角互补那么两直线平行
同旁内角互补两直线平行
3、(略)过程同上
【自主应用,高效准确】
1解:∠1=∠2
证明:∵∠1=∠2(已知)
∴AD∥BC(同位角相等两直线平行)
2-3、略
【拓展延伸,提升能力】
4、∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
证明:∵∠1=∠2(已知)
∴AB∥CD(内错角相等两直线平行)
∵∠3=1000,∠B=800(已知)
∴∠3+∠B=1800
∴AB∥EF(同旁内角互补两直线平行)
∴EF∥DC(平行于同一条直线的两直线互相平行)
5、证明:∵AB⊥BC,BC⊥CD
∴∠ABC=∠DCB=90°(垂直定义)
∵∠1=∠2(已知)
∴∠ABC-∠1=∠DCB-∠2(等式的性质)
即∠EBC=∠FCB ∴BE∥CF(内错角相等两直线平行)
【当堂巩固,达标测评】
1、 C 2、 C 3、 B
4 、(1)AF∥CE(内错角相等两直线平行)(2)AD∥BC(同位角相等两直线平行)(3)∠A+∠CDA=1800(同旁内角互补两直线平行)
5-6略
学习目标:
1.初步了解证明的基本步骤和书写格式.
2.会根据“同位角相等,两直线平行”证明平行线的其它判定定理,并能简单应用这些结论.
3.感受几何中推理的严谨性、结论的确定性,发展演绎推理的能力.
学习重点:平行线的判定定理的应用.
学习过程
一、复习检测:
1、公理的定义、定理的定义
2.平行线的判定公理.
3、平行线的识别方法有:(1) .
(2) ,(3)
4、如果两条直线都和第三条直线平行,那么这两条直线
5.如图,请你填写一个条件,使得DE∥BC
你填写的条件是
二、自主学习,小组交流:
自学课本84—85页内容后,小组内合作交流,讨论以下问题;
1.说一说怎样用三角板画平行线,根据是什么?与同伴交流.
2.已知:如图 ∠1,∠2是直线a和b被 直线c截出的同旁内角,
且∠1+∠2=180°
求证:a∥b
你证明的命题用文字叙述为
可以简单地叙述为
几何语言
3.已知:如图 ∠1,∠2是直线a和b被 直线c截出的内错角,
且∠1=∠2
求证:a∥b
你证明的命题用文字叙述为
可以简单地叙述为
几何语言
三、自主学习,合作探究:
1.当哪两个角相等时,AD∥BC?
写出你的推理过程.
2.如图已知:∠1=∠2
求证:AB∥CD
3..求证:垂直于同一条直线的两条直线互相平行.
四、巩固练习:
1.如图,由下列条件可判定两条直线平行,并说明根据
(1)∠1=∠2
(2)∠A=∠3
(3)∠ABC+∠C=1800
2.已知:如图,直线a,b被直线c所截,且∠1+∠2=1800
求证:a∥b
你有几种证明方法?
3.已知;如图,BP交CD与点P,∠ABP+∠BPC=1800,∠1=∠2
求证:EB∥PF
五、拓展延伸:
1、已知:如图∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
2. 如图:AB∥CD,∠1=1000,∠2=1200
求∠α的度数。
六、我的收获:(包括知识点、解题方法和技巧等方面)
七、达标检测:
1.下列命题中,假命题是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.同旁内角相等,两直线平行 D.同旁内角互补,两直线平行
2. 如图所示,下列条件中能判断直线AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠1+∠2=1800, D.∠3+∠4=900,
3.下列推理判断错误的是( )
A.∵∠1=∠2 ∴ a∥b, B.∵∠3+∠4=1800,∴ c∥d
C. ∵∠3=∠4 ∴ c∥d D.∵∠3+∠6=1800,∴ a∥b
4.填空:
(1)∵∠E=∠F ∴ ∥ ,( )
(2)∵∠A=∠FBC ∴ ∥ ,( )
(3)∵∠ +∠ =1800,∴ AB∥CD( )
5.光线经过玻璃砖发生折射,从玻璃砖出来的光线同样回发生折射, 如图,已知,∠1=∠4, ∠2=∠3
求证: c∥d
八、学(教)后反思:
参考答案
3.4 平行线的判定定理
一、课前准备
【预习检测】
1、(1)同位角相等两直线平行(2)内错角相等两直线平行(3)同旁内角互补两直线平行。2、互相平行。 3、∠ADE=∠ABC(答案不唯一)
二、课堂学习
【自主探究,同伴交流】
1略。2 、∵∠1+∠2=1800(已知)∠1+∠3=1800(1平角=1800)
∴∠2=∠3(等角的补角相等)
∴a∥b(同位角相等两直线平行)
两条直线被第三条直线截,如果同旁内角互补那么两直线平行
同旁内角互补两直线平行
3、(略)过程同上
【自主应用,高效准确】
1解:∠1=∠2
证明:∵∠1=∠2(已知)
∴AD∥BC(同位角相等两直线平行)
2-3、略
【拓展延伸,提升能力】
4、∠1=∠2,∠3=1000,∠B=800.
求证:EF∥DC
证明:∵∠1=∠2(已知)
∴AB∥CD(内错角相等两直线平行)
∵∠3=1000,∠B=800(已知)
∴∠3+∠B=1800
∴AB∥EF(同旁内角互补两直线平行)
∴EF∥DC(平行于同一条直线的两直线互相平行)
5、证明:∵AB⊥BC,BC⊥CD
∴∠ABC=∠DCB=90°(垂直定义)
∵∠1=∠2(已知)
∴∠ABC-∠1=∠DCB-∠2(等式的性质)
即∠EBC=∠FCB ∴BE∥CF(内错角相等两直线平行)
【当堂巩固,达标测评】
1、 C 2、 C 3、 B
4 、(1)AF∥CE(内错角相等两直线平行)(2)AD∥BC(同位角相等两直线平行)(3)∠A+∠CDA=1800(同旁内角互补两直线平行)
5-6略
