人教版八年级下17.1勾股定理(第2课时)课件(共15张PPT)
文档属性
| 名称 | 人教版八年级下17.1勾股定理(第2课时)课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 09:02:46 | ||
图片预览




文档简介
(共15张PPT)
17.1勾股定理(第2课时)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
1.已知在△ABC中,∠C=90°,若AC=12,BC=5,则AB=________
2.已知直角三角形两边分别为3,4,则第三边的长是
______
3.已知在△ABC 中,∠C=90°,AC=8,BC与AB的和是12,则BC的长是_______.
思考:勾股定理能帮助我们解决哪些问题?
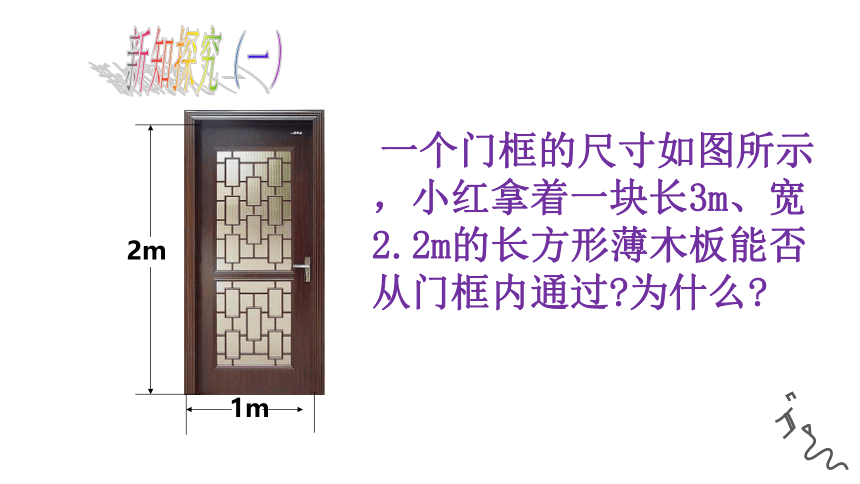
1m
2m
A
B
C
D
1 m
2 m
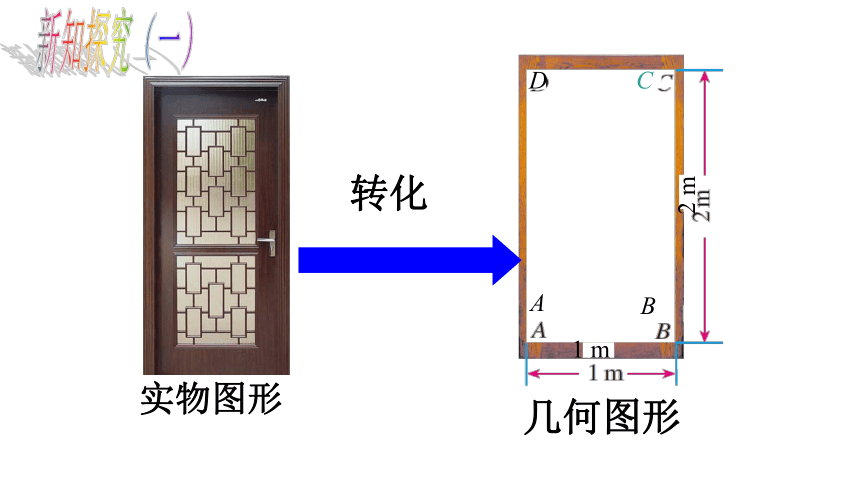
几何图形
实物图形
转化
A
B
C
D
1 m
2 m
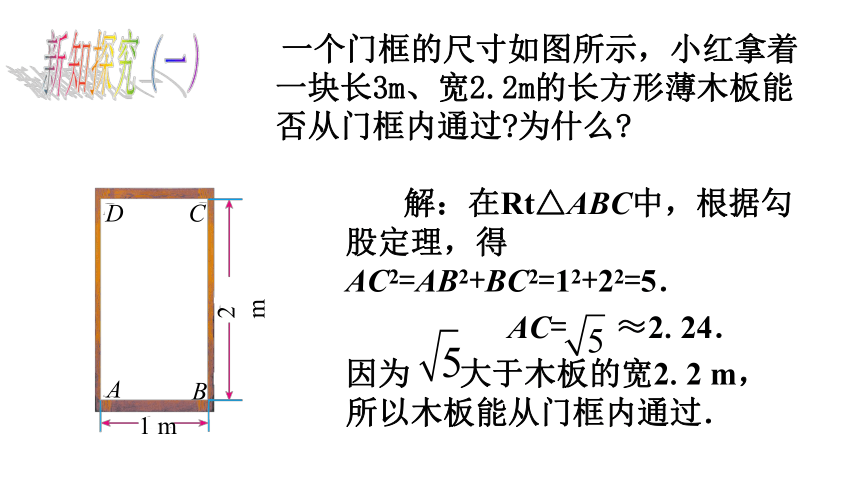
解:在Rt△ABC中,根据勾股定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以木板能从门框内通过.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架。它的代数成就主要包括开放术、正负术和方程术。其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈。问户高、广各几何?”(1丈=10尺,1尺=10寸)
设长方形门的宽x尺,可列方程:__________________.
如图,一个2.6米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B,也外移0.5m吗
解:(1)在Rt△AOB中,根据勾股定理,OB =AB -OA =2.6 -2.4 =1,OB=1
(2)在Rt△COD中,根据勾股定理,OD =CD -OC =2.6 -(2.4-0.5) =3.15
OD= ≈1.77
则BD=OD-OB≈1.77-1=0.77
1、一架2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
D
E
解:在Rt△ACB中,根据勾股定理,BC =AB -AC =2.5 -2.4 =0.49,OB=0.7
在RT△DCE中,根据勾股定理,CE =DE -CD =2.5 -(2.4-0.4) =2.25 CE=1.5 则BE=CE-OB=1.5-0.7=0.8
2、今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?
A
C
B
转化
实物图形
几何图形
解:设水池的深度AC为x尺,
则芦苇高AD=AB= (x+1)尺.
在Rt△ABC中,
由勾股定理得:
AC2+BC2=AB2
解得:
答:水池的深度为12尺,芦苇高为13尺.
1、一个人先向东走了9米,又向南走了12米,此时他距离起点_____米,他走了_____米.
2、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了____________m.
(结果保留根号)
3、在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
A
C
B
6米
8 米
你觉得解决实际问题的难点在哪里?你有什么 好的突破办法?利用勾股定理解决实际问题的注意点是什么?请与大家交流.
必做题:教材28页17.1第3、5题
选做题:教材29页17.1第12,13题
17.1勾股定理(第2课时)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
1.已知在△ABC中,∠C=90°,若AC=12,BC=5,则AB=________
2.已知直角三角形两边分别为3,4,则第三边的长是
______
3.已知在△ABC 中,∠C=90°,AC=8,BC与AB的和是12,则BC的长是_______.
思考:勾股定理能帮助我们解决哪些问题?
1m
2m
A
B
C
D
1 m
2 m
几何图形
实物图形
转化
A
B
C
D
1 m
2 m
解:在Rt△ABC中,根据勾股定理,得 AC2=AB2+BC2=12+22=5.
AC= ≈2.24.
因为 大于木板的宽2.2 m,所以木板能从门框内通过.
《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架。它的代数成就主要包括开放术、正负术和方程术。其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈。问户高、广各几何?”(1丈=10尺,1尺=10寸)
设长方形门的宽x尺,可列方程:__________________.
如图,一个2.6米长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B,也外移0.5m吗
解:(1)在Rt△AOB中,根据勾股定理,OB =AB -OA =2.6 -2.4 =1,OB=1
(2)在Rt△COD中,根据勾股定理,OD =CD -OC =2.6 -(2.4-0.5) =3.15
OD= ≈1.77
则BD=OD-OB≈1.77-1=0.77
1、一架2.5m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.4m.如果梯子顶端A沿墙下滑0.4m,那么梯子底端B也外移0.4m吗?
D
E
解:在Rt△ACB中,根据勾股定理,BC =AB -AC =2.5 -2.4 =0.49,OB=0.7
在RT△DCE中,根据勾股定理,CE =DE -CD =2.5 -(2.4-0.4) =2.25 CE=1.5 则BE=CE-OB=1.5-0.7=0.8
2、今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何?
A
C
B
转化
实物图形
几何图形
解:设水池的深度AC为x尺,
则芦苇高AD=AB= (x+1)尺.
在Rt△ABC中,
由勾股定理得:
AC2+BC2=AB2
解得:
答:水池的深度为12尺,芦苇高为13尺.
1、一个人先向东走了9米,又向南走了12米,此时他距离起点_____米,他走了_____米.
2、长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了____________m.
(结果保留根号)
3、在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处。你能告诉小明这棵树折断之前有多高吗?
A
C
B
6米
8 米
你觉得解决实际问题的难点在哪里?你有什么 好的突破办法?利用勾股定理解决实际问题的注意点是什么?请与大家交流.
必做题:教材28页17.1第3、5题
选做题:教材29页17.1第12,13题
