2.6相似三角形的性质
图片预览
文档简介
课题
2.6相似三角形的性质(一)
授课人
教学目标
(一)知识技能:①经历探索相似三角形性质的过程②理解并掌握相似三角形中,对应高、对应角平分线、对应中线的比都等于其相似比。
(二)数学思考:①通过探索相似三角形的性质体会模型思想,类比的方法等。②在研究相似三角形性质的过程中,进一步发展学生的空间观念及推理能力。
(三)问题解决:在探索相似三角形性质的过程中,发展学生提出问题、分析问题、解决问题的能力,能应用相似三角形的性质解决一些简单的实际问题。
(四)情感态度:通过主动研究、合作交流,感受探索的乐趣和成功体验,养成积极思考、独立克服困难的好习惯,培养学生参与意识和团队意识。
重点
相似三角形的性质,
运用相似三角形的性质解决实际问题。
难点
相似三角形性质的应用、例2
教学活动
学生活动
一、回顾练习
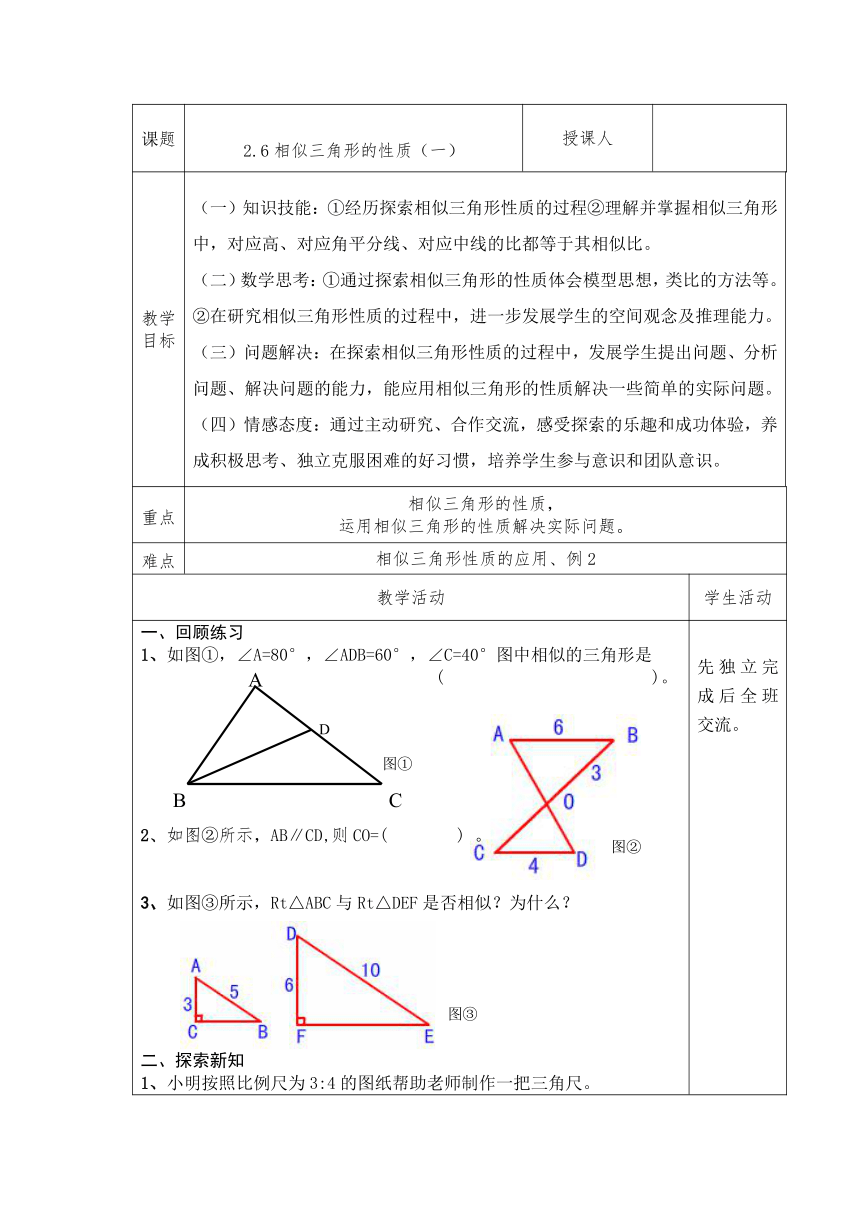
1、如图①,∠A=80°,∠ADB=60°,∠C=40°图中相似的三角形是
( )。
2、如图②所示,AB∥CD,则CO=( ) 。
3、如图③所示,Rt△ABC与Rt△DEF是否相似?为什么?
二、探索新知
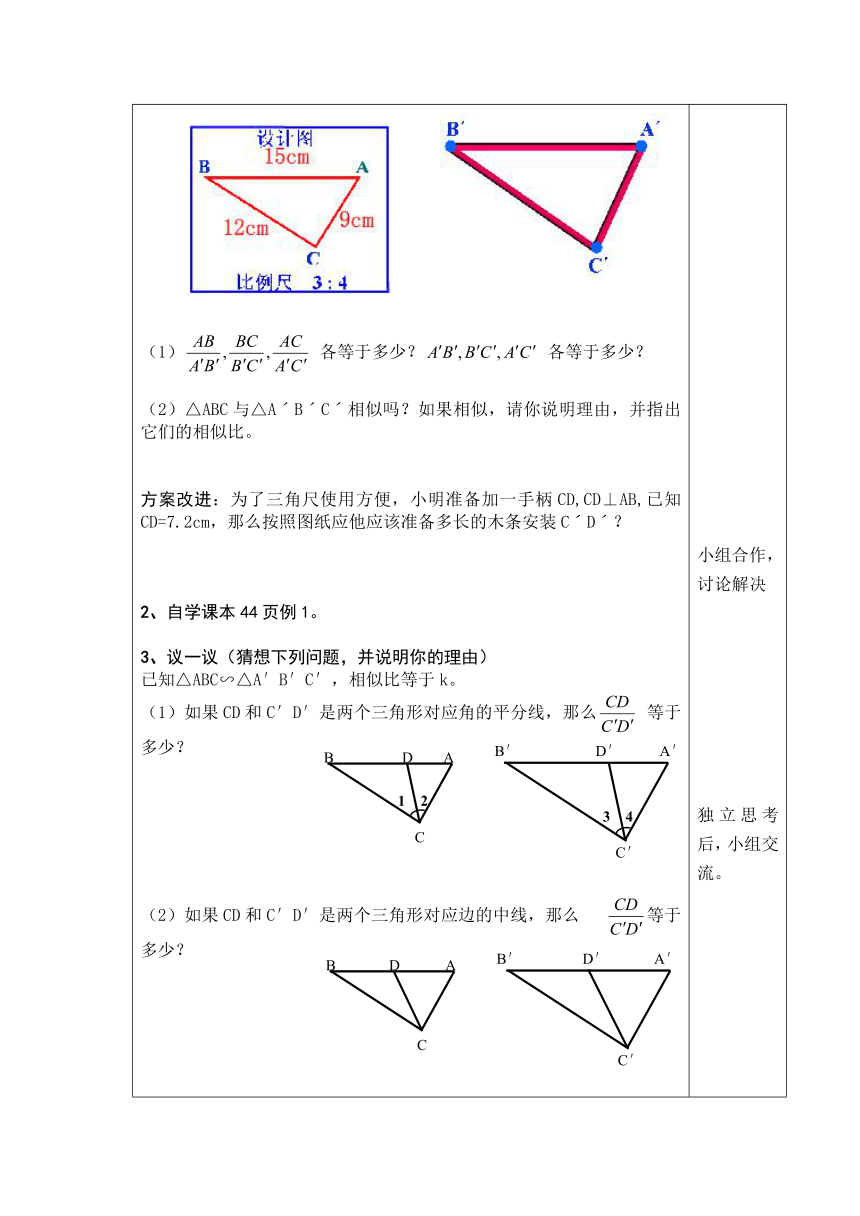
1、小明按照比例尺为3:4的图纸帮助老师制作一把三角尺。
(1) 各等于多少? 各等于多少?
(2)△ABC与△AˊBˊCˊ相似吗?如果相似,请你说明理由,并指出它们的相似比。
方案改进:为了三角尺使用方便,小明准备加一手柄CD,CD⊥AB,已知CD=7.2cm,那么按照图纸应他应该准备多长的木条安装CˊDˊ?
2、自学课本44页例1。
3、议一议(猜想下列问题,并说明你的理由)
已知△ABC∽△A′B′C′,相似比等于k。
(1)如果CD和C′D′是两个三角形对应角的平分线,那么 等于多少?
(2)如果CD和C′D′是两个三角形对应边的中线,那么 等于多少?
三、巩固运用:
1、已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,, B′D′=4cm,BD=( ).
2、已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,AD=8cm,A′D′=3cm,那么△ABC与△A′B′C′的对应高的比为( )。
四、学习例2:
例2 如图,在△ABC中,边BC=60cm,高AD=40cm,正方形PQRS的一边PQ在BC上,另两个顶点S,R分别在AB,AC上,SR与AD相交于点E.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长。
五、变式训练
如图所示,在△ABC中,边BC=60cm,高AD=40cm,若将例2中的正方形PQRS变成长与宽的比为2﹕1的矩形,要求短边PQ在BC上,求矩形的长与宽。
六、感悟与反思
这节课你学习了哪些知识?
有什么需要注意的问题?
收获了哪些良好的学习方法和习惯......
七、检测反馈(相信自我 展现风采)
1、如图所示,EF∥BC,AD⊥BC,垂足为D,
,AD=6,则AM=( ).
2、两个相似三角形的对应角平分线的比为,则对应高的比为( ),对应中线的比为( )。
3、如图,小明自制了一个小孔成像装置,一支长为20cm的蜡烛AB所成的像CD为5cm(AB∥CD),已知像CD到装置的距离为15cm,那么蜡烛距离装置有( )cm。
A、15 B、30 C、45 D、60
八、布置作业:
1、新课堂同步练习1、2(必作)
2、新课堂观察与思考(选作)
3、预习作业:相似三角形的面积比、周长比与相似比的关系。
先独立完成后全班交流。
小组合作,
讨论解决
独立思考后,小组交流。
独立完成后发言交流。
先小组合作互助探究,后全班交流
独立完成后全班交流
2.6相似三角形的性质(一)
授课人
教学目标
(一)知识技能:①经历探索相似三角形性质的过程②理解并掌握相似三角形中,对应高、对应角平分线、对应中线的比都等于其相似比。
(二)数学思考:①通过探索相似三角形的性质体会模型思想,类比的方法等。②在研究相似三角形性质的过程中,进一步发展学生的空间观念及推理能力。
(三)问题解决:在探索相似三角形性质的过程中,发展学生提出问题、分析问题、解决问题的能力,能应用相似三角形的性质解决一些简单的实际问题。
(四)情感态度:通过主动研究、合作交流,感受探索的乐趣和成功体验,养成积极思考、独立克服困难的好习惯,培养学生参与意识和团队意识。
重点
相似三角形的性质,
运用相似三角形的性质解决实际问题。
难点
相似三角形性质的应用、例2
教学活动
学生活动
一、回顾练习
1、如图①,∠A=80°,∠ADB=60°,∠C=40°图中相似的三角形是
( )。
2、如图②所示,AB∥CD,则CO=( ) 。
3、如图③所示,Rt△ABC与Rt△DEF是否相似?为什么?
二、探索新知
1、小明按照比例尺为3:4的图纸帮助老师制作一把三角尺。
(1) 各等于多少? 各等于多少?
(2)△ABC与△AˊBˊCˊ相似吗?如果相似,请你说明理由,并指出它们的相似比。
方案改进:为了三角尺使用方便,小明准备加一手柄CD,CD⊥AB,已知CD=7.2cm,那么按照图纸应他应该准备多长的木条安装CˊDˊ?
2、自学课本44页例1。
3、议一议(猜想下列问题,并说明你的理由)
已知△ABC∽△A′B′C′,相似比等于k。
(1)如果CD和C′D′是两个三角形对应角的平分线,那么 等于多少?
(2)如果CD和C′D′是两个三角形对应边的中线,那么 等于多少?
三、巩固运用:
1、已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,, B′D′=4cm,BD=( ).
2、已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,AD=8cm,A′D′=3cm,那么△ABC与△A′B′C′的对应高的比为( )。
四、学习例2:
例2 如图,在△ABC中,边BC=60cm,高AD=40cm,正方形PQRS的一边PQ在BC上,另两个顶点S,R分别在AB,AC上,SR与AD相交于点E.
(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长。
五、变式训练
如图所示,在△ABC中,边BC=60cm,高AD=40cm,若将例2中的正方形PQRS变成长与宽的比为2﹕1的矩形,要求短边PQ在BC上,求矩形的长与宽。
六、感悟与反思
这节课你学习了哪些知识?
有什么需要注意的问题?
收获了哪些良好的学习方法和习惯......
七、检测反馈(相信自我 展现风采)
1、如图所示,EF∥BC,AD⊥BC,垂足为D,
,AD=6,则AM=( ).
2、两个相似三角形的对应角平分线的比为,则对应高的比为( ),对应中线的比为( )。
3、如图,小明自制了一个小孔成像装置,一支长为20cm的蜡烛AB所成的像CD为5cm(AB∥CD),已知像CD到装置的距离为15cm,那么蜡烛距离装置有( )cm。
A、15 B、30 C、45 D、60
八、布置作业:
1、新课堂同步练习1、2(必作)
2、新课堂观察与思考(选作)
3、预习作业:相似三角形的面积比、周长比与相似比的关系。
先独立完成后全班交流。
小组合作,
讨论解决
独立思考后,小组交流。
独立完成后发言交流。
先小组合作互助探究,后全班交流
独立完成后全班交流
