高中数学苏教版(2019 )选择性必修第二册 第8章 概率 章末复习课学案
文档属性
| 名称 | 高中数学苏教版(2019 )选择性必修第二册 第8章 概率 章末复习课学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 435.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览



文档简介
章末复习课
一、条件概率与全概率公式
1.求条件概率有两种方法:一种是基于样本空间Ω,先计算P(A)和P(AB),再利用P(B|A)=求解;另一种是缩小样本空间,即以A为样本空间计算AB的概率.
2.掌握条件概率与全概率运算,重点提升逻辑推理和数学运算的核心素养.
例1 采购员要购买10个一包的电器元件.他的采购方法是:从一包中随机抽查3个,如果这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品.求:
(1)采购员拒绝购买的概率;
(2)在采购员拒绝购买的条件下,抽中的一包中含有4个次品的概率.
解 B1={取到的是含4个次品的包},
B2={取到的是含1个次品的包},
A={采购员拒绝购买},
P(B1)=,P(B2)=.
P(A|B1)=1-=,
P(A|B2)=1-=.
(1)由全概率公式得到
P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)
=×+×=.
(2)P(B1|A)===.
反思感悟 条件概率的计算要注意以下三点:
(1)明白是在谁的条件下,计算谁的概率.
(2)明确P(A),P(B|A)以及P(AB)三者间的关系,实现三者间的互化.
(3)理解全概率公式P(A)=(Bi)P(A|Bi)中化整为零的计算思想.
跟踪训练1 某小组有20名射手,其中1,2,3,4级射手分别为2,6,9,3名.又若选1,2,3,4级射手参加比赛,则在比赛中射中目标的概率分别为0.85,0.64,0.45,0.32,今随机选一人参加比赛,则该小组比赛中射中目标的概率为( )
A.0.542 2 B.0.612 3
C.0.527 5 D.0.324 5
答案 C
解析 设B表示“该小组比赛中射中目标”,
Ai(i=1,2,3,4)表示“选i级射手参加比赛”,
则P(B)=(Ai)P(B|Ai)
=×0.85+×0.64+×0.45+×0.32=0.527 5.
二、离散型随机变量的概率分布、均值和方差
1.均值和方差都是随机变量的重要的数字特征,方差是建立在均值的基础之上,它表明了随机变量所取的值相对于它的均值的集中与离散程度,二者的联系密切,在现实生产生活中的应用比较广泛.
2.通过求离散型随机变量的概率分布,培养数学运算、逻辑推理等核心素养.
角度1 均值、方差的计算
例2 某学院为了调查本校学生4月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图如图所示.
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的概率分布及均值E(Y).
解 (1)由图可知健康上网天数未超过20天的频率为(0.01+0.02+0.03+0.09)×5=0.15×5=0.75,所以健康上网天数超过20天的学生人数是40×(1-0.75)=40×0.25=10.
(2)随机变量Y的所有可能取值为0,1,2,
且Y服从超几何分布.
所以P(Y=0)==,
P(Y=1)==,
P(Y=2)==.
所以Y的概率分布为
Y 0 1 2
P
所以Y的均值E(Y)=1×+2×=.
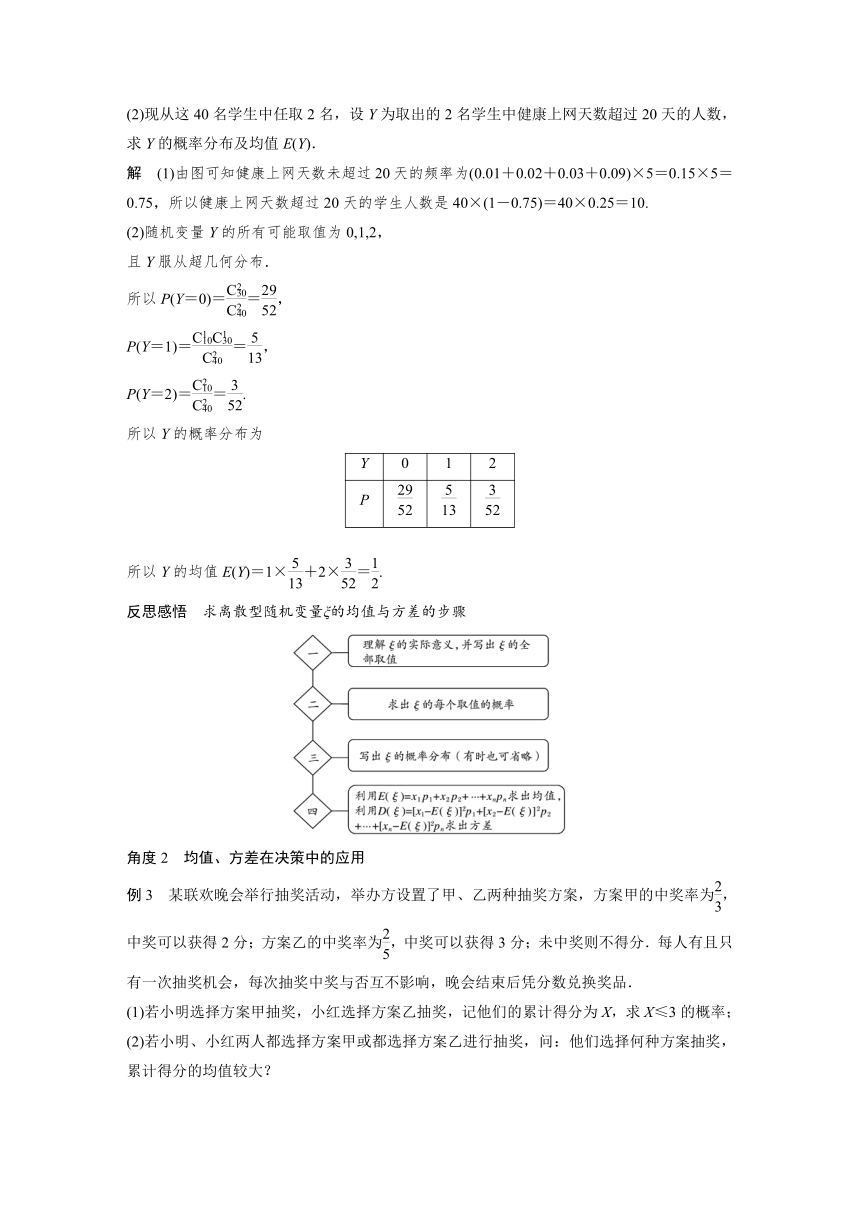
反思感悟 求离散型随机变量ξ的均值与方差的步骤
角度2 均值、方差在决策中的应用
例3 某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为,中奖可以获得2分;方案乙的中奖率为,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
解 (1)由已知得,小明中奖的概率为,小红中奖的概率为,两人中奖与否互不影响,记“这2人的累计得分X≤3”的事件为A,则A事件的对立事件为“X=5”.
∵P(X=5)=×=,
∴P(A)=1-P(X=5)=,
∴这两人的累计得分X≤3的概率为.
(2)设小明、小红都选择方案甲抽奖中奖的次数为X1,都选择方案乙抽奖中奖的次数为X2,则这两人选择方案甲抽奖累计得分的均值为E(2X1),选择方案乙抽奖累计得分的均值为E(3X2),
由已知,X1~B,X2~B,
∴E(X1)=2×=,E(X2)=2×=.
∴E(2X1)=2E(X1)=,E(3X2)=3E(X2)=.
E(2X1)>E(3X2),他们都选择方案甲进行抽奖时,累计得分的均值最大.
反思感悟 若X~B(n,p),则可直接利用公式求,E(X)=np,D(X)=np(1-p).
跟踪训练2 甲、乙、丙3人投篮,投进的概率分别是,,.
(1)现3人各投篮1次,求3人都没有投进的概率;
(2)用ξ表示乙投篮10次的进球数,求随机变量ξ的概率分布及均值E(ξ)和方差D(ξ);
(3)若η=4ξ+1.求E(η)和D(η).
解 (1)记“甲投篮1次投进”为事件A1,“乙投篮1次投进”为事件A2,“丙投篮1次投进”为事件A3,“3人都没有投进”为事件A.
则P(A1)=,P(A2)=,
P(A3)=,
所以P(A)=P(123)
=P(1)·P(2)·P(3)
=[1-P(A1)]·[1-P(A2)]·[1-P(A3)]
==.
(2)根据题意ξ~B,其概率分布为P(ξ=k)=C·k·10-k(k=0,1,2,…,10),
E(ξ)=10×=4,
D(ξ)=10××=.
(3)E(η)=4E(ξ)+1=4×4+1=17,
D(η)=16·D(ξ)=16×=.
三、正态分布
1.正态分布是连续型随机变量X的一种分布,其在概率和统计中占有重要地位,尤其统计学中的3σ原则在生产生活中有广泛的应用.
2.熟记正态分布的特征及应用3σ原则解决实际问题是本章的两个重点,在学习中提升直观想象、数据分析的素养.
例4 为提高城市居民生活幸福感,某城市公交公司大力确保公交车的准点率,减少居民侯车时间,为此,该公司对某站台乘客的候车时间进行统计.乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响.在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,乘客候车时间X服从正态分布N(μ,σ2).在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图所示的频率分布直方图.
(1)在直方图各组中,以该组区间的中点值代表该组的各个值,试估计μ,σ2的值;
(2)在统计学中,发生概率低于千分之三的事件叫小概率事件,一般认为,在正常情况下,一次试验中,小概率事件是不能发生的.在交通拥堵情况正常、非节假日的某天,随机调查了该站的10名乘客的候车时间,发现其中有3名乘客候车时间超过15分钟,试判断该天公交车准点率是否正常,说明理由.
(参考数据:≈4.38,≈4.63,≈5.16,0.841 57≈0.298 8,0.841 56≈0.355 1,0.158 53≈0.004 0,0.158 54≈0.000 6,P(μ-σ解 (1)μ=0.1×2+0.2×6+0.4×10+0.2×14+0.1×18=10,
σ2=s2=2×(82×0.1+42×0.2)+(10-10)2×0.4=19.2.
(2)由(1)知σ≈4.38,
∴μ+σ=10+4.38=14.38,
P(X>14.38)=≈0.158 5,
设“3名乘客候车时间超过15分钟”的事件为A,
P(A)=C×(0.158 5)3×(0.841 5)7≈0.143>0.003,
准点率正常.
反思感悟 利用正态曲线解决实际性问题时常利用其对称性解题,并注意借助(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)三个区间内的概率值求解.并注意正态曲线与频率分布直方图的结合.
跟踪训练3 某市为了解本市1万名小学生的普通话水平,在全市范围内进行了普通话测试,测试后对每个小学生的普通话测试成绩进行统计,发现总体(这1万名小学生普通话测试成绩)服从正态分布N(69,49).
(1)从这1万名小学生中任意抽取1名小学生,求这名小学生的普通话测试成绩在(62,90)内的概率;
(2)现在从总体中随机抽取12名小学生的普通话测试成绩,对应的数据如下:50,52,56,62,63,68,65,64,72,80,67,90.从这12个数据中随机选取4个,记X表示大于总体平均分的个数,求X的方差.
参考数据:若Y~N(μ,σ2),则P(μ-σ解 (1)因为学生的普通话测试成绩Y服从正态分布N(69,49),所以μ=69,σ=7,
所以P(62≈=0.84.
(2)因为总体平均分为μ=69,
所以这12个数据中大于总体平均分的有3个,
所以X的可能取值为0,1,2,3,
则P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
所以E(X)=0×+1×+2×+3×=1,
D(X)=(0-1)2×+(1-1)2×+(2-1)2×+(3-1)2×=.
1.投掷一枚质地均匀的骰子两次,记事件A表示“两次的点数均为奇数”,事件B表示“两次的点数之和为4”,则P(B|A)等于( )
A. B.
C. D.
答案 C
解析 由题意知事件A包含的样本点是(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9个,在A发生的条件下,事件B包含的样本点是(1,3),(3,1),共2个,所以P(B|A)=.
2.设随机变量X的概率分布为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B.
C.2 D.4
答案 C
解析 E(X)=-1×+0×+1×=0,D(X)=(-1-0)2×+(0-0)2×+(1-0)2×=,D(Y)=D(2X+2)=4D(X)=4×=2.
3.一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则D(X)=________.
答案 1.96
解析 由题意得X~B(100,0.02),
∴D(X)=100×0.02×(1-0.02)=1.96.
4.下列命题中,正确的命题序号为________.
①已知随机变量X服从二项分布B(n,p),若E(X)=30,D(X)=20,则p=;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ≤0)=-p;
④某人在10次射击中,击中目标的次数为X,X~B(10,0.8),则当X=8时概率最大.
答案 ②③④
解析 根据二项分布的均值和方差的公式,
可得E(X)=np=30,D(X)=np(1-p)=20,
解得p=,所以①错误;
根据数据方差的计算公式可知,将一组数据中的每个数据都加上同一个常数后,方差恒不变,所以②正确;
由正态分布的图象的对称性可得P(-1<ξ≤0)===-p,所以③正确;
由n重伯努利试验的概率的计算公式可得P(X=8)=C·(0.8)8(1-0.8)2,
由组合数的公式,可得当X=8时取得最大值,所以④正确.
一、条件概率与全概率公式
1.求条件概率有两种方法:一种是基于样本空间Ω,先计算P(A)和P(AB),再利用P(B|A)=求解;另一种是缩小样本空间,即以A为样本空间计算AB的概率.
2.掌握条件概率与全概率运算,重点提升逻辑推理和数学运算的核心素养.
例1 采购员要购买10个一包的电器元件.他的采购方法是:从一包中随机抽查3个,如果这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品.求:
(1)采购员拒绝购买的概率;
(2)在采购员拒绝购买的条件下,抽中的一包中含有4个次品的概率.
解 B1={取到的是含4个次品的包},
B2={取到的是含1个次品的包},
A={采购员拒绝购买},
P(B1)=,P(B2)=.
P(A|B1)=1-=,
P(A|B2)=1-=.
(1)由全概率公式得到
P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)
=×+×=.
(2)P(B1|A)===.
反思感悟 条件概率的计算要注意以下三点:
(1)明白是在谁的条件下,计算谁的概率.
(2)明确P(A),P(B|A)以及P(AB)三者间的关系,实现三者间的互化.
(3)理解全概率公式P(A)=(Bi)P(A|Bi)中化整为零的计算思想.
跟踪训练1 某小组有20名射手,其中1,2,3,4级射手分别为2,6,9,3名.又若选1,2,3,4级射手参加比赛,则在比赛中射中目标的概率分别为0.85,0.64,0.45,0.32,今随机选一人参加比赛,则该小组比赛中射中目标的概率为( )
A.0.542 2 B.0.612 3
C.0.527 5 D.0.324 5
答案 C
解析 设B表示“该小组比赛中射中目标”,
Ai(i=1,2,3,4)表示“选i级射手参加比赛”,
则P(B)=(Ai)P(B|Ai)
=×0.85+×0.64+×0.45+×0.32=0.527 5.
二、离散型随机变量的概率分布、均值和方差
1.均值和方差都是随机变量的重要的数字特征,方差是建立在均值的基础之上,它表明了随机变量所取的值相对于它的均值的集中与离散程度,二者的联系密切,在现实生产生活中的应用比较广泛.
2.通过求离散型随机变量的概率分布,培养数学运算、逻辑推理等核心素养.
角度1 均值、方差的计算
例2 某学院为了调查本校学生4月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图如图所示.
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的概率分布及均值E(Y).
解 (1)由图可知健康上网天数未超过20天的频率为(0.01+0.02+0.03+0.09)×5=0.15×5=0.75,所以健康上网天数超过20天的学生人数是40×(1-0.75)=40×0.25=10.
(2)随机变量Y的所有可能取值为0,1,2,
且Y服从超几何分布.
所以P(Y=0)==,
P(Y=1)==,
P(Y=2)==.
所以Y的概率分布为
Y 0 1 2
P
所以Y的均值E(Y)=1×+2×=.
反思感悟 求离散型随机变量ξ的均值与方差的步骤
角度2 均值、方差在决策中的应用
例3 某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为,中奖可以获得2分;方案乙的中奖率为,中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
解 (1)由已知得,小明中奖的概率为,小红中奖的概率为,两人中奖与否互不影响,记“这2人的累计得分X≤3”的事件为A,则A事件的对立事件为“X=5”.
∵P(X=5)=×=,
∴P(A)=1-P(X=5)=,
∴这两人的累计得分X≤3的概率为.
(2)设小明、小红都选择方案甲抽奖中奖的次数为X1,都选择方案乙抽奖中奖的次数为X2,则这两人选择方案甲抽奖累计得分的均值为E(2X1),选择方案乙抽奖累计得分的均值为E(3X2),
由已知,X1~B,X2~B,
∴E(X1)=2×=,E(X2)=2×=.
∴E(2X1)=2E(X1)=,E(3X2)=3E(X2)=.
E(2X1)>E(3X2),他们都选择方案甲进行抽奖时,累计得分的均值最大.
反思感悟 若X~B(n,p),则可直接利用公式求,E(X)=np,D(X)=np(1-p).
跟踪训练2 甲、乙、丙3人投篮,投进的概率分别是,,.
(1)现3人各投篮1次,求3人都没有投进的概率;
(2)用ξ表示乙投篮10次的进球数,求随机变量ξ的概率分布及均值E(ξ)和方差D(ξ);
(3)若η=4ξ+1.求E(η)和D(η).
解 (1)记“甲投篮1次投进”为事件A1,“乙投篮1次投进”为事件A2,“丙投篮1次投进”为事件A3,“3人都没有投进”为事件A.
则P(A1)=,P(A2)=,
P(A3)=,
所以P(A)=P(123)
=P(1)·P(2)·P(3)
=[1-P(A1)]·[1-P(A2)]·[1-P(A3)]
==.
(2)根据题意ξ~B,其概率分布为P(ξ=k)=C·k·10-k(k=0,1,2,…,10),
E(ξ)=10×=4,
D(ξ)=10××=.
(3)E(η)=4E(ξ)+1=4×4+1=17,
D(η)=16·D(ξ)=16×=.
三、正态分布
1.正态分布是连续型随机变量X的一种分布,其在概率和统计中占有重要地位,尤其统计学中的3σ原则在生产生活中有广泛的应用.
2.熟记正态分布的特征及应用3σ原则解决实际问题是本章的两个重点,在学习中提升直观想象、数据分析的素养.
例4 为提高城市居民生活幸福感,某城市公交公司大力确保公交车的准点率,减少居民侯车时间,为此,该公司对某站台乘客的候车时间进行统计.乘客候车时间受公交车准点率、交通拥堵情况、节假日人流量增大等情况影响.在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,乘客候车时间X服从正态分布N(μ,σ2).在公交车准点率正常、交通拥堵情况正常、非节假日的情况下,调查了大量乘客的候车时间,经过统计得到如图所示的频率分布直方图.
(1)在直方图各组中,以该组区间的中点值代表该组的各个值,试估计μ,σ2的值;
(2)在统计学中,发生概率低于千分之三的事件叫小概率事件,一般认为,在正常情况下,一次试验中,小概率事件是不能发生的.在交通拥堵情况正常、非节假日的某天,随机调查了该站的10名乘客的候车时间,发现其中有3名乘客候车时间超过15分钟,试判断该天公交车准点率是否正常,说明理由.
(参考数据:≈4.38,≈4.63,≈5.16,0.841 57≈0.298 8,0.841 56≈0.355 1,0.158 53≈0.004 0,0.158 54≈0.000 6,P(μ-σ
σ2=s2=2×(82×0.1+42×0.2)+(10-10)2×0.4=19.2.
(2)由(1)知σ≈4.38,
∴μ+σ=10+4.38=14.38,
P(X>14.38)=≈0.158 5,
设“3名乘客候车时间超过15分钟”的事件为A,
P(A)=C×(0.158 5)3×(0.841 5)7≈0.143>0.003,
准点率正常.
反思感悟 利用正态曲线解决实际性问题时常利用其对称性解题,并注意借助(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)三个区间内的概率值求解.并注意正态曲线与频率分布直方图的结合.
跟踪训练3 某市为了解本市1万名小学生的普通话水平,在全市范围内进行了普通话测试,测试后对每个小学生的普通话测试成绩进行统计,发现总体(这1万名小学生普通话测试成绩)服从正态分布N(69,49).
(1)从这1万名小学生中任意抽取1名小学生,求这名小学生的普通话测试成绩在(62,90)内的概率;
(2)现在从总体中随机抽取12名小学生的普通话测试成绩,对应的数据如下:50,52,56,62,63,68,65,64,72,80,67,90.从这12个数据中随机选取4个,记X表示大于总体平均分的个数,求X的方差.
参考数据:若Y~N(μ,σ2),则P(μ-σ
所以P(62
(2)因为总体平均分为μ=69,
所以这12个数据中大于总体平均分的有3个,
所以X的可能取值为0,1,2,3,
则P(X=0)==,
P(X=1)==,
P(X=2)==,
P(X=3)==,
所以E(X)=0×+1×+2×+3×=1,
D(X)=(0-1)2×+(1-1)2×+(2-1)2×+(3-1)2×=.
1.投掷一枚质地均匀的骰子两次,记事件A表示“两次的点数均为奇数”,事件B表示“两次的点数之和为4”,则P(B|A)等于( )
A. B.
C. D.
答案 C
解析 由题意知事件A包含的样本点是(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9个,在A发生的条件下,事件B包含的样本点是(1,3),(3,1),共2个,所以P(B|A)=.
2.设随机变量X的概率分布为
X -1 0 1
P
若Y=2X+2,则D(Y)等于( )
A.- B.
C.2 D.4
答案 C
解析 E(X)=-1×+0×+1×=0,D(X)=(-1-0)2×+(0-0)2×+(1-0)2×=,D(Y)=D(2X+2)=4D(X)=4×=2.
3.一批产品的二等品率为0.02,从这批产品中每次随机取一件,有放回地抽取100次,X表示抽到的二等品件数,则D(X)=________.
答案 1.96
解析 由题意得X~B(100,0.02),
∴D(X)=100×0.02×(1-0.02)=1.96.
4.下列命题中,正确的命题序号为________.
①已知随机变量X服从二项分布B(n,p),若E(X)=30,D(X)=20,则p=;
②将一组数据中的每个数据都加上同一个常数后,方差恒不变;
③设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ≤0)=-p;
④某人在10次射击中,击中目标的次数为X,X~B(10,0.8),则当X=8时概率最大.
答案 ②③④
解析 根据二项分布的均值和方差的公式,
可得E(X)=np=30,D(X)=np(1-p)=20,
解得p=,所以①错误;
根据数据方差的计算公式可知,将一组数据中的每个数据都加上同一个常数后,方差恒不变,所以②正确;
由正态分布的图象的对称性可得P(-1<ξ≤0)===-p,所以③正确;
由n重伯努利试验的概率的计算公式可得P(X=8)=C·(0.8)8(1-0.8)2,
由组合数的公式,可得当X=8时取得最大值,所以④正确.
