勾股定理第一课(说课课件)PPT课件
文档属性
| 名称 | 勾股定理第一课(说课课件)PPT课件 |  | |
| 格式 | zip | ||
| 文件大小 | 119.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-08 15:38:30 | ||
图片预览






文档简介
课件17张PPT。《勾股定理》
一、 教材分析
二、教法与学法分析
三、 教学过程设计
四、 设计说明
一、 教材分析(一)教材所处的地位
(二)本课的教学目标
1、认识目标
2、能力目标
3、情感目标
(三)本课的教学重点与难点
(二)本课的教学目标 1、认识目标:能说出勾股定理的内容;会初步运用勾股定理进行简单的计算和实际运用。2、能力目标:在探索勾股定理的过程中,让学生经历“实验—观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法;在勾股定理的运用中,渗透“方程观点”,提高学生正确、灵活应用勾股定理的能力。
3、情感目标:通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
(三)本课的教学重点与难点
教学重点:勾股定理及其应用
教学难点:勾股定理的证明 三、 教学过程设计 (一)创设情境----引入新课
(二)动手操作----探求新知
(三)证明结论----得到定理
(四)文字概括----揭示主题
(五)例题讲解----知识应用
(六)巩固练习----测评反馈
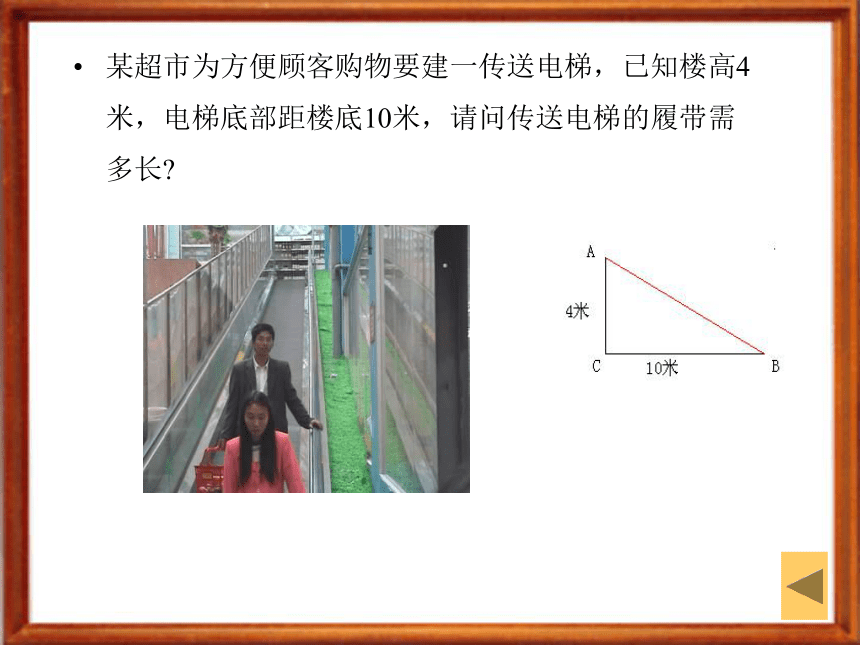
(七)总结反思 ----形成结构某超市为方便顾客购物要建一传送电梯,已知楼高4米,电梯底部距楼底10米,请问传送电梯的履带需多长?证明结论----得到定理?
S正方形ABCD
= 4× ab+a2+b2
S正方形方形A`B`C`D`
= 4× ab+c2
所以4× ab+ a2+b2
= 4× ab+ c2
从而有a2+b2= c2加菲尔德S四边形A C` D` C = (a+b)(a+b)
= (a+b)2
S四边形A C` D` C
= a?b+ a?b+ c2
从而 (a+b)2 =a?b+ c2
得到a2+b2=c2
例1:在Rt△ABC中,∠C=90o
(1)??? 已知a=b=5,求c;
(2)??? 已知a=1, c=2,求b;
(3)??? 已知c=17,b=8,求a;
(4)??? 已知a:b=1:2,且c=5求a、b;例2:某超市为方便顾客购物要建一传送电梯,已知楼高4米,电梯底部距楼底10米,请问传送电梯的履带需多长? 思考练习已知一个直角三角形的两边长分别为5㎝和12㎝,求第三边长。布置作业 1、阅读课本P96~98;这样有助于学生对本课教学的内容加深理解和记忆。
2、必做题目:课本P104第2、4题。
选做题:P106页B组题第一题。
3、阅读材料后,写读后感。(阅读材料根据P107页给出的网址下载)。
四、 设计说明 1、教学流程是:引入新课—动手操作—证明结论—文字概括—例题讲解—巩固练习—总结反思七部分
2、板书设计分为三个部分:第一部分为学生拼图的展示区;第二部分为勾股定理内容;第三部分是定理的运用----例题讲解。
3、时间大致安排:复习引入约三分钟,实验操作约十分钟,归纳验证约五分钟,例题讲解约十五分钟,巩固练习约七分钟,小结作业约五分钟 。
板书设计 3.16勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。拼图展示区
学生板演
例1勾股定理:例2谢 谢 大 家, 再 见!
二、教法与学法分析
三、 教学过程设计
四、 设计说明
一、 教材分析(一)教材所处的地位
(二)本课的教学目标
1、认识目标
2、能力目标
3、情感目标
(三)本课的教学重点与难点
(二)本课的教学目标 1、认识目标:能说出勾股定理的内容;会初步运用勾股定理进行简单的计算和实际运用。2、能力目标:在探索勾股定理的过程中,让学生经历“实验—观察—猜想—归纳—验证”的数学思想,并体会数形结合和特殊到一般的思想方法;在勾股定理的运用中,渗透“方程观点”,提高学生正确、灵活应用勾股定理的能力。
3、情感目标:通过介绍勾股定理在中国古代的研究,激发学生热爱祖国,热爱祖国悠久文化的思想,激励学生发奋学习。
(三)本课的教学重点与难点
教学重点:勾股定理及其应用
教学难点:勾股定理的证明 三、 教学过程设计 (一)创设情境----引入新课
(二)动手操作----探求新知
(三)证明结论----得到定理
(四)文字概括----揭示主题
(五)例题讲解----知识应用
(六)巩固练习----测评反馈
(七)总结反思 ----形成结构某超市为方便顾客购物要建一传送电梯,已知楼高4米,电梯底部距楼底10米,请问传送电梯的履带需多长?证明结论----得到定理?
S正方形ABCD
= 4× ab+a2+b2
S正方形方形A`B`C`D`
= 4× ab+c2
所以4× ab+ a2+b2
= 4× ab+ c2
从而有a2+b2= c2加菲尔德S四边形A C` D` C = (a+b)(a+b)
= (a+b)2
S四边形A C` D` C
= a?b+ a?b+ c2
从而 (a+b)2 =a?b+ c2
得到a2+b2=c2
例1:在Rt△ABC中,∠C=90o
(1)??? 已知a=b=5,求c;
(2)??? 已知a=1, c=2,求b;
(3)??? 已知c=17,b=8,求a;
(4)??? 已知a:b=1:2,且c=5求a、b;例2:某超市为方便顾客购物要建一传送电梯,已知楼高4米,电梯底部距楼底10米,请问传送电梯的履带需多长? 思考练习已知一个直角三角形的两边长分别为5㎝和12㎝,求第三边长。布置作业 1、阅读课本P96~98;这样有助于学生对本课教学的内容加深理解和记忆。
2、必做题目:课本P104第2、4题。
选做题:P106页B组题第一题。
3、阅读材料后,写读后感。(阅读材料根据P107页给出的网址下载)。
四、 设计说明 1、教学流程是:引入新课—动手操作—证明结论—文字概括—例题讲解—巩固练习—总结反思七部分
2、板书设计分为三个部分:第一部分为学生拼图的展示区;第二部分为勾股定理内容;第三部分是定理的运用----例题讲解。
3、时间大致安排:复习引入约三分钟,实验操作约十分钟,归纳验证约五分钟,例题讲解约十五分钟,巩固练习约七分钟,小结作业约五分钟 。
板书设计 3.16勾股定理
直角三角形两直角边a、b的平方和等于斜边c的平方。拼图展示区
学生板演
例1勾股定理:例2谢 谢 大 家, 再 见!
