2021—2022学年人教版八年级数学下册第十八章平行四边形单元测试题(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册第十八章平行四边形单元测试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 260.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览

文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形 单元测试题
一、选择题(30分)
1.甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅要他们拿尺子帮助检测一个窗框是否是矩形,他们各自做了如下检测,你认为最有说服力的是( )
A.甲量得窗框的一组邻边相等
B.乙量得窗框两组对边分别相等
C.丙量得窗框的对角线长相等
D.丁量得窗框的两组对边分别相等且两条对角线也相等
2.菱形ABCD的边长为5,一条对角线长为6,则菱形面积为( )
A.20 B.24 C.30 D.48
3.平行四边形ABCD中,若∠A=2∠B,则∠C的度数为( )
A.120° B.60° C.30° D.15°
4.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
5.如图,菱形ABCD的面积为24cm2,对角线BD长6cm,点O为BD的中点,过点A作AE⊥BC交CB的延长线于点E,连接OE,则线段OE的长度是( )
A.3cm B.4cm C.4.8cm D.5cm
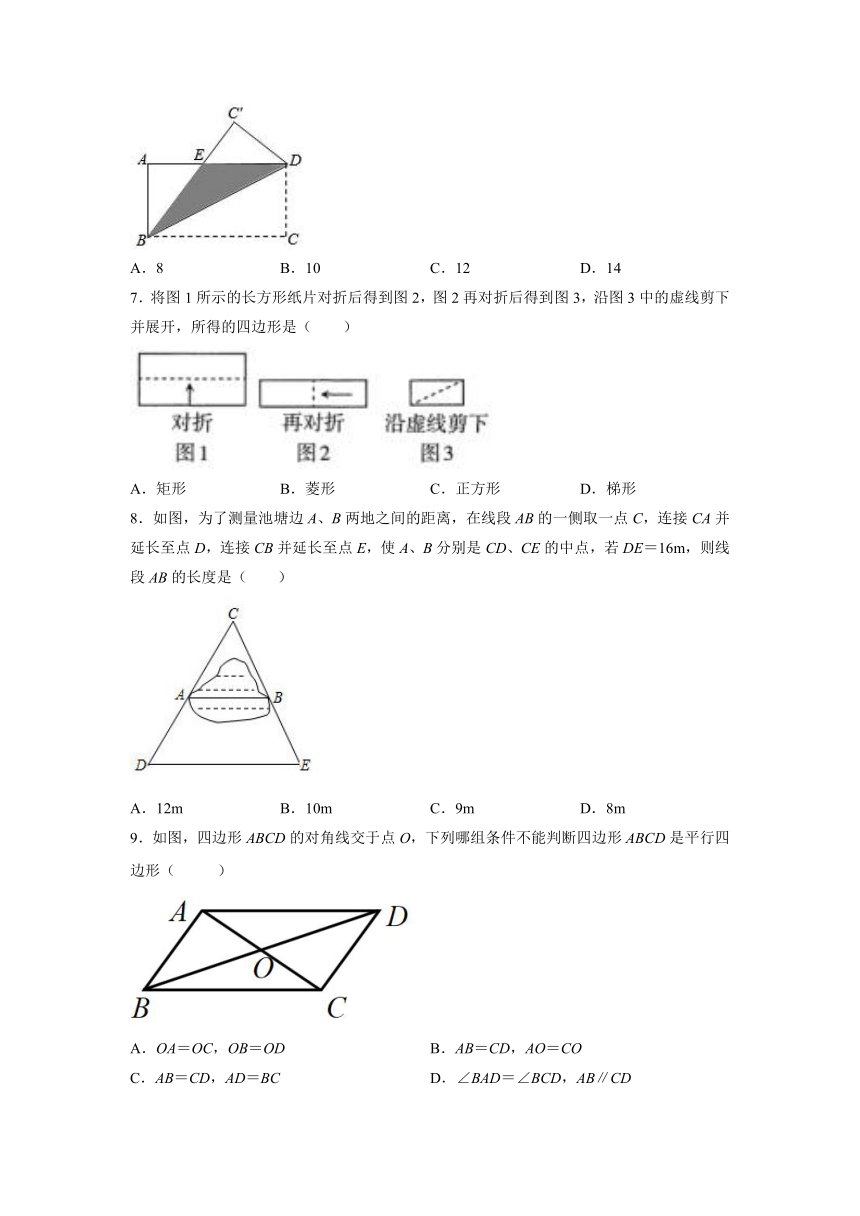
6.如图,矩形中,,如果将该矩形沿对角线折叠,那么图中阴影部分的面积是22.5,则( )
A.8 B.10 C.12 D.14
7.将图1所示的长方形纸片对折后得到图2,图2再对折后得到图3,沿图3中的虚线剪下并展开,所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.梯形
8.如图,为了测量池塘边A、B两地之间的距离,在线段AB的一侧取一点C,连接CA并延长至点D,连接CB并延长至点E,使A、B分别是CD、CE的中点,若DE=16m,则线段AB的长度是( )
A.12m B.10m C.9m D.8m
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD
10.如图,在平行四边形ABCD中,,,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A.1 B.2 C.3 D.4
二、填空题(15分)
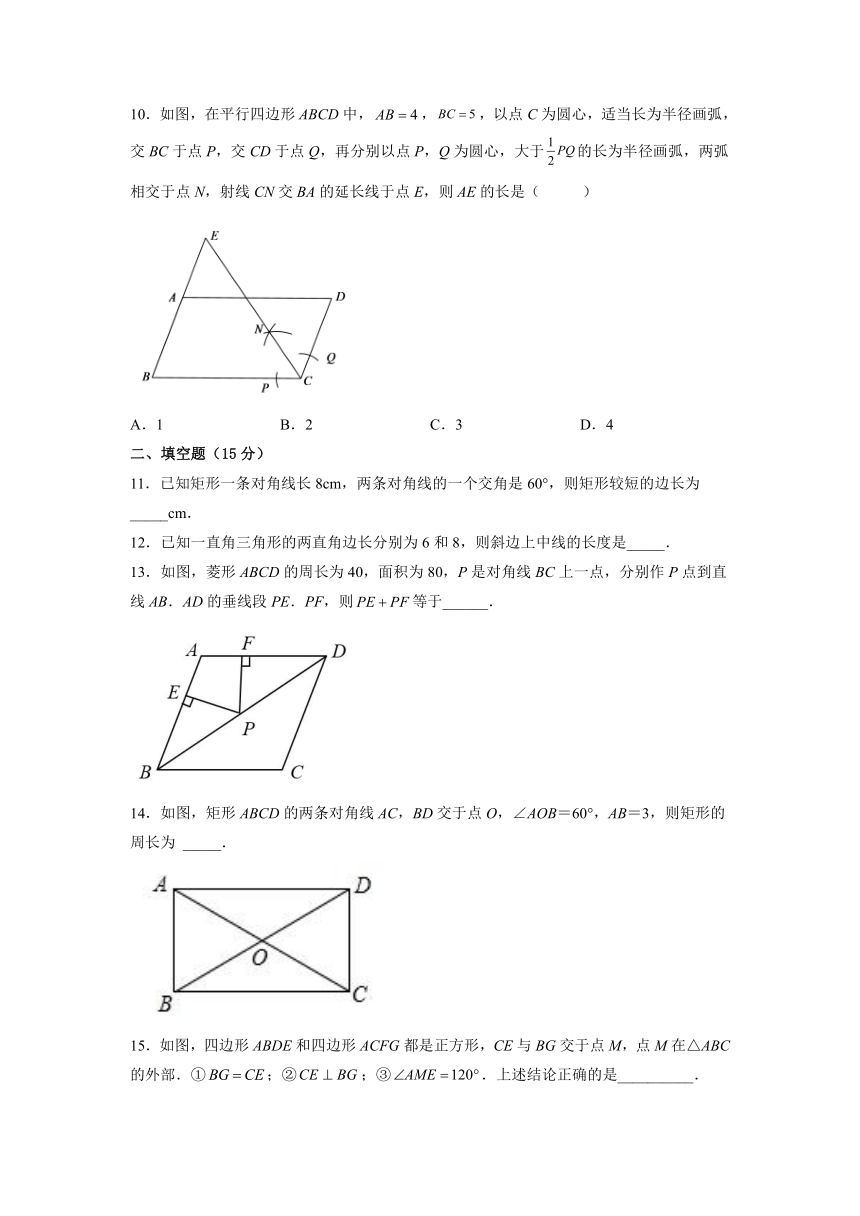
11.已知矩形一条对角线长8cm,两条对角线的一个交角是60°,则矩形较短的边长为 _____cm.
12.已知一直角三角形的两直角边长分别为6和8,则斜边上中线的长度是_____.
13.如图,菱形ABCD的周长为40,面积为80,P是对角线BC上一点,分别作P点到直线AB.AD的垂线段PE.PF,则等于______.
14.如图,矩形ABCD的两条对角线AC,BD交于点O,∠AOB=60°,AB=3,则矩形的周长为 _____.
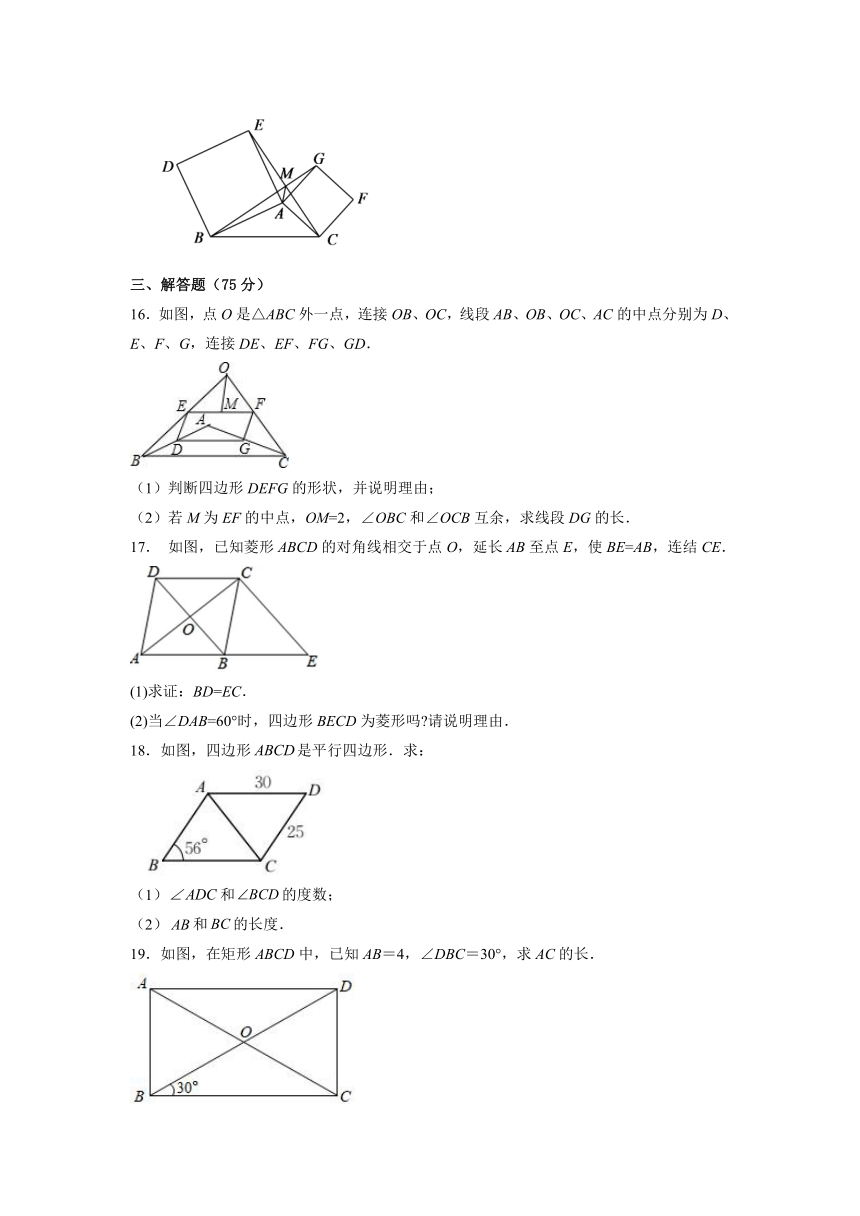
15.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.①;②;③.上述结论正确的是__________.
三、解答题(75分)
16.如图,点O是△ABC外一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G,连接DE、EF、FG、GD.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段DG的长.
17. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)当∠DAB=60°时,四边形BECD为菱形吗 请说明理由.
18.如图,四边形是平行四边形.求:
(1)和的度数;
(2)和的长度.
19.如图,在矩形ABCD中,已知AB=4,∠DBC=30°,求AC的长.
20.如图,在中,点E,H,F,G分别在边上,,,与相交于点O,图中共有多少个平行四边形?
21.如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出的中点M,N,并测出的长,如果M,N两点之间还有阻隔,你有什么解决办法?说明你的理由.
22.如图,在平行四边形中,过点作于点,点在边上,且,连接、.
(1)求证:四边形是矩形;
(2)若平分,,,求的长.
23.如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
【参考答案】
1.D 2.B 3.A 4.D 5.B 6.C 7.B 8.D 9.B 10.A
11.4
12.5
13.8
14.
15.①②
16.解:(1)四边形DEFG是平行四边形,
理由是:∵线段AB、OB、OC、AC的中点分别为D、E、F、G,
∴EF∥BC,EF=BC,DG∥BC,DG=BC,
∴EF∥DG,EF=DG,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=180°﹣90°=90°,
∴∠EOF=90°,△EOF为直角三角形,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∵EF=DG,
∴DG=4.
17.(1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:结论:四边形BECD是菱形.
理由:∵四边形ABCD是菱形,
∴AD=AB,
∵∠DAB=60°,
∴△ADB,△DCB都是等边三角形,
∴DC=DB,
∵四边形BECD是平行四边形,
∴四边形BECD是菱形.
18.解:(1)∵四边形ABCD是平行四边形
∴ ,
∵
∴
(2)∵四边形ABCD是平行四边形
∴
∵
∴
19.解:∵四边形ABCD是矩形,
∴CD=AB=4,AC=BD,∠BCD=90°,
又∵∠DBC=30°,
∴BD=2CD=2×4=8,
∴AC=8.
20.四边形是平行四边形,
,
,,
平行四边形有:ABCD,ABHG,CDGH,BCFE,ADFE,AGOE,BEOH,OFCH,OGDF共9个,
共有9个平行四边形.
21.解:用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,
∵点D、E分别为CM,CN的中点,
∴DE=(三角形的中位线平行于第三边,并且等于第三边的一半),
又∵点M,N分别为的中点,
∴MN=(三角形的中位线平行于第三边,并且等于第三边的一半),
∴AB=2MN=4DE.
∴只要测量出DE长便可求AB.
22.解:(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
即,
∴四边形是平行四边形,
又∵,
∴,
∴平行四边形是矩形;
(2)∵平分,
∴,
∵,
∴,
∴,
∴,
在中,,由勾股定理得:
,
由(1)得四边形是矩形,
∴.
23.(1)证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴
一、选择题(30分)
1.甲、乙、丙、丁四位同学到木工厂参观时,一木工师傅要他们拿尺子帮助检测一个窗框是否是矩形,他们各自做了如下检测,你认为最有说服力的是( )
A.甲量得窗框的一组邻边相等
B.乙量得窗框两组对边分别相等
C.丙量得窗框的对角线长相等
D.丁量得窗框的两组对边分别相等且两条对角线也相等
2.菱形ABCD的边长为5,一条对角线长为6,则菱形面积为( )
A.20 B.24 C.30 D.48
3.平行四边形ABCD中,若∠A=2∠B,则∠C的度数为( )
A.120° B.60° C.30° D.15°
4.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为8,则OH的长为( )
A.4 B.3 C.2 D.1
5.如图,菱形ABCD的面积为24cm2,对角线BD长6cm,点O为BD的中点,过点A作AE⊥BC交CB的延长线于点E,连接OE,则线段OE的长度是( )
A.3cm B.4cm C.4.8cm D.5cm
6.如图,矩形中,,如果将该矩形沿对角线折叠,那么图中阴影部分的面积是22.5,则( )
A.8 B.10 C.12 D.14
7.将图1所示的长方形纸片对折后得到图2,图2再对折后得到图3,沿图3中的虚线剪下并展开,所得的四边形是( )
A.矩形 B.菱形 C.正方形 D.梯形
8.如图,为了测量池塘边A、B两地之间的距离,在线段AB的一侧取一点C,连接CA并延长至点D,连接CB并延长至点E,使A、B分别是CD、CE的中点,若DE=16m,则线段AB的长度是( )
A.12m B.10m C.9m D.8m
9.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD B.AB=CD,AO=CO
C.AB=CD,AD=BC D.∠BAD=∠BCD,AB∥CD
10.如图,在平行四边形ABCD中,,,以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是( )
A.1 B.2 C.3 D.4
二、填空题(15分)
11.已知矩形一条对角线长8cm,两条对角线的一个交角是60°,则矩形较短的边长为 _____cm.
12.已知一直角三角形的两直角边长分别为6和8,则斜边上中线的长度是_____.
13.如图,菱形ABCD的周长为40,面积为80,P是对角线BC上一点,分别作P点到直线AB.AD的垂线段PE.PF,则等于______.
14.如图,矩形ABCD的两条对角线AC,BD交于点O,∠AOB=60°,AB=3,则矩形的周长为 _____.
15.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.①;②;③.上述结论正确的是__________.
三、解答题(75分)
16.如图,点O是△ABC外一点,连接OB、OC,线段AB、OB、OC、AC的中点分别为D、E、F、G,连接DE、EF、FG、GD.
(1)判断四边形DEFG的形状,并说明理由;
(2)若M为EF的中点,OM=2,∠OBC和∠OCB互余,求线段DG的长.
17. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC.
(2)当∠DAB=60°时,四边形BECD为菱形吗 请说明理由.
18.如图,四边形是平行四边形.求:
(1)和的度数;
(2)和的长度.
19.如图,在矩形ABCD中,已知AB=4,∠DBC=30°,求AC的长.
20.如图,在中,点E,H,F,G分别在边上,,,与相交于点O,图中共有多少个平行四边形?
21.如图,A,B两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出了A,B间的距离:先在外选一点C,然后步测出的中点M,N,并测出的长,如果M,N两点之间还有阻隔,你有什么解决办法?说明你的理由.
22.如图,在平行四边形中,过点作于点,点在边上,且,连接、.
(1)求证:四边形是矩形;
(2)若平分,,,求的长.
23.如图,在四边形ABCD中,,,对角线AC、BD交于点O,AC平分∠BAD,过点C作交AB的延长线于点E.
(1)求证:四边形ABCD是菱形;
(2)若,,求CE的长.
【参考答案】
1.D 2.B 3.A 4.D 5.B 6.C 7.B 8.D 9.B 10.A
11.4
12.5
13.8
14.
15.①②
16.解:(1)四边形DEFG是平行四边形,
理由是:∵线段AB、OB、OC、AC的中点分别为D、E、F、G,
∴EF∥BC,EF=BC,DG∥BC,DG=BC,
∴EF∥DG,EF=DG,
∴四边形DEFG是平行四边形;
(2)∵∠OBC和∠OCB互余,
∴∠OBC+∠OCB=90°,
∴∠BOC=180°﹣90°=90°,
∴∠EOF=90°,△EOF为直角三角形,
∵M为EF的中点,OM=2,
∴EF=2OM=4,
∵EF=DG,
∴DG=4.
17.(1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:结论:四边形BECD是菱形.
理由:∵四边形ABCD是菱形,
∴AD=AB,
∵∠DAB=60°,
∴△ADB,△DCB都是等边三角形,
∴DC=DB,
∵四边形BECD是平行四边形,
∴四边形BECD是菱形.
18.解:(1)∵四边形ABCD是平行四边形
∴ ,
∵
∴
(2)∵四边形ABCD是平行四边形
∴
∵
∴
19.解:∵四边形ABCD是矩形,
∴CD=AB=4,AC=BD,∠BCD=90°,
又∵∠DBC=30°,
∴BD=2CD=2×4=8,
∴AC=8.
20.四边形是平行四边形,
,
,,
平行四边形有:ABCD,ABHG,CDGH,BCFE,ADFE,AGOE,BEOH,OFCH,OGDF共9个,
共有9个平行四边形.
21.解:用步测出CM,CN中点D、E, 只要测量出DE长便可求出AB,
∵点D、E分别为CM,CN的中点,
∴DE=(三角形的中位线平行于第三边,并且等于第三边的一半),
又∵点M,N分别为的中点,
∴MN=(三角形的中位线平行于第三边,并且等于第三边的一半),
∴AB=2MN=4DE.
∴只要测量出DE长便可求AB.
22.解:(1)证明:∵四边形是平行四边形,
∴,,
∵,
∴,
即,
∴四边形是平行四边形,
又∵,
∴,
∴平行四边形是矩形;
(2)∵平分,
∴,
∵,
∴,
∴,
∴,
在中,,由勾股定理得:
,
由(1)得四边形是矩形,
∴.
23.(1)证明:∵,
∴,
∵AC平分∠BAD,
∴,
∴,
∴,
∵AB=AD,
∴,
∵,
∴四边形ABCD是平行四边形,
又∵,
∴四边形ABCD是菱形;
(2)∵四边形ABCD是菱形,BD=6,AC=8,
∴,,,
∴,
在中,根据勾股定理可知,
,
∴菱形的面积,
∵,
∴菱形面积,
∴
