2021-2022学年人教版七年级数学下册5.4平移练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.4平移练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 297.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览




文档简介
5.4 平移
一、单选题
1.下列图形不能通过平移变换得到的是( )
A. B.
C. D.
2.下列生活现象中,属于平移的是( )
A.足球在草地上滚动 B.拉开抽屈
C.把打开的课本合上 D.钟摆的摆动
3.如图,若三角形ABC是由三角形DEF经过平移后得到的,则平移的距离( )
A.线段BC的长度 B.线段BE的长度
C.线段EC的长度 D.线段EF的长度
4.下列说法不正确的是( )
A.平移不改变图形的形状和大小
B.平移中图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形的对应点的连接线段平行且相等
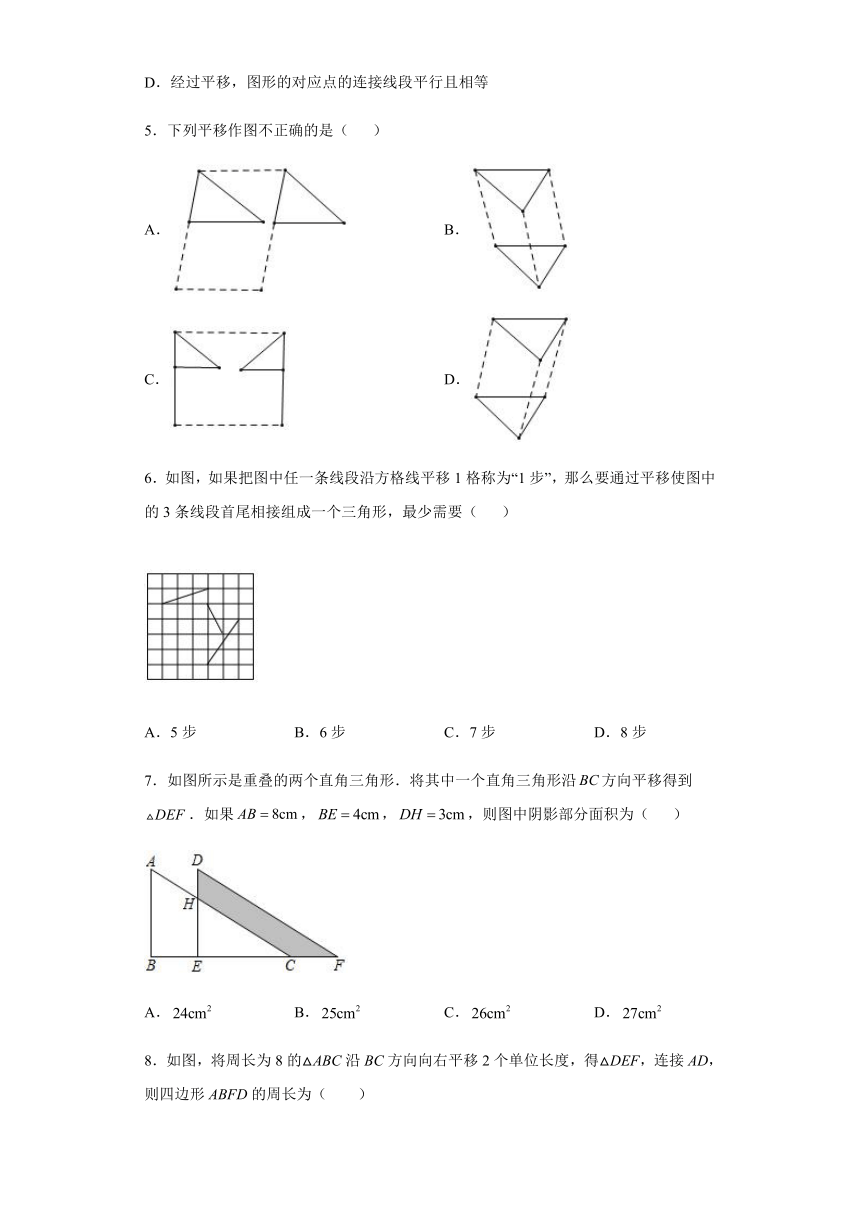
5.下列平移作图不正确的是( )
A. B.
C. D.
6.如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要( )
A.5步 B.6步 C.7步 D.8步
7.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿方向平移得到.如果,,,则图中阴影部分面积为( )
A. B. C. D.
8.如图,将周长为8的△ABC沿BC方向向右平移2个单位长度,得△DEF,连接AD,则四边形ABFD的周长为( )
A.10 B.12 C.14 D.16
9.如图,在长为m,宽为m的长方形草地中有两条小路,和、为状,为平行四边形状,每条小路的右边线都是由小路左边线右移m得到的,两条小路、占地面积的情况是( )
A.占地面积大 B.占地面积大
C.和占地面积一样大 D.无法确定
10.如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
二、填空题
11.如图,线段CD可以看成由线段AB先向下平移______个单位,再向右平移______个单位得到.
12.在下列图案中可以用平移得到的是______(填代号).
13.如图,直角三角形ABC的周长为2021,在其内部有5个小直角三角形,则这5个小直角三角形周长的和为____.
14.如图,在△ABC中,,将△ABC以每秒2cm的速度沿所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使成立,则的值为_____秒.
三、解答题
15.如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
16.如图,的网格中,每个小方格的边长为一个单位,将向右平移2格,再向下平移1格,得.
(1)画出;
(2)线段与的大小关系为__________;
(3)与的位置关系为__________;
(4)求的面积.
17.如图,将水平向右平移得到,,两点的距离为1,,.根据题意完成下列各题:
(1)和的数量关系为__________;和的位置关系为___________;
(2)求的度数;
(3)__________.
18.如图所示,一块长方形地板,长为60cm,宽为40cm,上面横竖各有两道宽为5cm的花纹(图中阴影部分),那么空白部分的面积是多少?
19.已知点C在射线OA上.
(1)如图①,CDOE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;
(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)
(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.
试卷第1页,共3页
答案
1.B
2.B
3.B
4.B
5.C
6.A
7.C
8.B
9.C
10.D
11. 2 2
12.③④⑤
13.2021
14.2或6.
15.解:(1)如图,连接,平移的方向是点A到点D的方向,平移的距离是线段的长度.
(2)如图,过点B,C分别作线段,使得它们与线段平行且相等,连接,就是平移后的图形.
16.解:(1)如图,△A′B′C′即为所求.
(2)由平移的性质可得:BC=B′C′.
故答案为:BC=B′C′.
(3)由平移的性质可得:AA′∥BB′
故答案为:AA′∥BB′.
(4)S△A′B′C′=2×3×1×3×1×1×2×2=2.
17.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
故答案为:AC=DF,AC∥DF;
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110°;
(3)BF=BE+CE+CF=1+2+1=4.
故答案为:4.
18.解:(40-2×5)×(60-2×5),
=30×50,
=1500(平方厘米);
答:空白部分的面积是1500平方厘米.
19.解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-∠AOE-∠AOB=360°-90°-120°=150°;
(2)∠OCD+∠BO′E′=360°-α.
证明:如图②,过O点作OF∥CD,
∵CD∥O′E′,
∴OF∥O′E′,
∴∠AOF=180°-∠OCD,∠BOF=∠E′O′O=180°-∠BO′E′,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E′=360°-(∠OCD+∠BO′E′)=α,
∴∠OCD+∠BO′E′=360°-α;
(3)∠AOB=∠BO′E′.
证明:∵∠CPO′=90°,
∴PO′⊥CP,
∵PO′⊥OB,
∴CP∥OB,
∴∠PCO+∠AOB=180°,
∴2∠PCO=360°-2∠AOB,
∵CP是∠OCD的平分线,
∴∠OCD=2∠PCO=360°-2∠AOB,
∵由(2)知,∠OCD+∠BO′E′=360°-α=360°-∠AOB,
∴360°-2∠AOB+∠BO′E′=360°-∠AOB,
∴∠AOB=∠BO′E′.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列图形不能通过平移变换得到的是( )
A. B.
C. D.
2.下列生活现象中,属于平移的是( )
A.足球在草地上滚动 B.拉开抽屈
C.把打开的课本合上 D.钟摆的摆动
3.如图,若三角形ABC是由三角形DEF经过平移后得到的,则平移的距离( )
A.线段BC的长度 B.线段BE的长度
C.线段EC的长度 D.线段EF的长度
4.下列说法不正确的是( )
A.平移不改变图形的形状和大小
B.平移中图形上每个点移动的距离可以不同
C.经过平移,图形的对应线段、对应角分别相等
D.经过平移,图形的对应点的连接线段平行且相等
5.下列平移作图不正确的是( )
A. B.
C. D.
6.如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要( )
A.5步 B.6步 C.7步 D.8步
7.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿方向平移得到.如果,,,则图中阴影部分面积为( )
A. B. C. D.
8.如图,将周长为8的△ABC沿BC方向向右平移2个单位长度,得△DEF,连接AD,则四边形ABFD的周长为( )
A.10 B.12 C.14 D.16
9.如图,在长为m,宽为m的长方形草地中有两条小路,和、为状,为平行四边形状,每条小路的右边线都是由小路左边线右移m得到的,两条小路、占地面积的情况是( )
A.占地面积大 B.占地面积大
C.和占地面积一样大 D.无法确定
10.如图,从甲地到乙地有三条路线:①甲→A→D→乙;②甲→B→D→乙;③甲→B→C→乙,在这三条路线中,走哪条路线近?答案是( )
A.① B.①② C.①③ D.①②③
二、填空题
11.如图,线段CD可以看成由线段AB先向下平移______个单位,再向右平移______个单位得到.
12.在下列图案中可以用平移得到的是______(填代号).
13.如图,直角三角形ABC的周长为2021,在其内部有5个小直角三角形,则这5个小直角三角形周长的和为____.
14.如图,在△ABC中,,将△ABC以每秒2cm的速度沿所在直线向右平移,所得图形对应为△DEF,设平移时间为t秒,若要使成立,则的值为_____秒.
三、解答题
15.如图,经过平移,的顶点A移到了点D.
(1)指出平移的方向和平移的距离;
(2)画出平移后的三角形.
16.如图,的网格中,每个小方格的边长为一个单位,将向右平移2格,再向下平移1格,得.
(1)画出;
(2)线段与的大小关系为__________;
(3)与的位置关系为__________;
(4)求的面积.
17.如图,将水平向右平移得到,,两点的距离为1,,.根据题意完成下列各题:
(1)和的数量关系为__________;和的位置关系为___________;
(2)求的度数;
(3)__________.
18.如图所示,一块长方形地板,长为60cm,宽为40cm,上面横竖各有两道宽为5cm的花纹(图中阴影部分),那么空白部分的面积是多少?
19.已知点C在射线OA上.
(1)如图①,CDOE,若∠AOB=90°,∠OCD=120°,求∠BOE的度数;
(2)在①中,将射线OE沿射线OB平移得O′E'(如图②),若∠AOB=α,探究∠OCD与∠BO′E′的关系(用含α的代数式表示)
(3)在②中,过点O′作OB的垂线,与∠OCD的平分线交于点P(如图③),若∠CPO′=90°,探究∠AOB与∠BO′E′的关系.
试卷第1页,共3页
答案
1.B
2.B
3.B
4.B
5.C
6.A
7.C
8.B
9.C
10.D
11. 2 2
12.③④⑤
13.2021
14.2或6.
15.解:(1)如图,连接,平移的方向是点A到点D的方向,平移的距离是线段的长度.
(2)如图,过点B,C分别作线段,使得它们与线段平行且相等,连接,就是平移后的图形.
16.解:(1)如图,△A′B′C′即为所求.
(2)由平移的性质可得:BC=B′C′.
故答案为:BC=B′C′.
(3)由平移的性质可得:AA′∥BB′
故答案为:AA′∥BB′.
(4)S△A′B′C′=2×3×1×3×1×1×2×2=2.
17.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
故答案为:AC=DF,AC∥DF;
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110°;
(3)BF=BE+CE+CF=1+2+1=4.
故答案为:4.
18.解:(40-2×5)×(60-2×5),
=30×50,
=1500(平方厘米);
答:空白部分的面积是1500平方厘米.
19.解:(1)∵CD∥OE,
∴∠AOE=∠OCD=120°,
∴∠BOE=360°-∠AOE-∠AOB=360°-90°-120°=150°;
(2)∠OCD+∠BO′E′=360°-α.
证明:如图②,过O点作OF∥CD,
∵CD∥O′E′,
∴OF∥O′E′,
∴∠AOF=180°-∠OCD,∠BOF=∠E′O′O=180°-∠BO′E′,
∴∠AOB=∠AOF+∠BOF=180°-∠OCD+180°-∠BO′E′=360°-(∠OCD+∠BO′E′)=α,
∴∠OCD+∠BO′E′=360°-α;
(3)∠AOB=∠BO′E′.
证明:∵∠CPO′=90°,
∴PO′⊥CP,
∵PO′⊥OB,
∴CP∥OB,
∴∠PCO+∠AOB=180°,
∴2∠PCO=360°-2∠AOB,
∵CP是∠OCD的平分线,
∴∠OCD=2∠PCO=360°-2∠AOB,
∵由(2)知,∠OCD+∠BO′E′=360°-α=360°-∠AOB,
∴360°-2∠AOB+∠BO′E′=360°-∠AOB,
∴∠AOB=∠BO′E′.
答案第1页,共2页
答案第1页,共2页
