2021-2022学年人教版八年级数学下册18.2.1矩形的判定同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2.1矩形的判定同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 92.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览


文档简介
矩形的判定
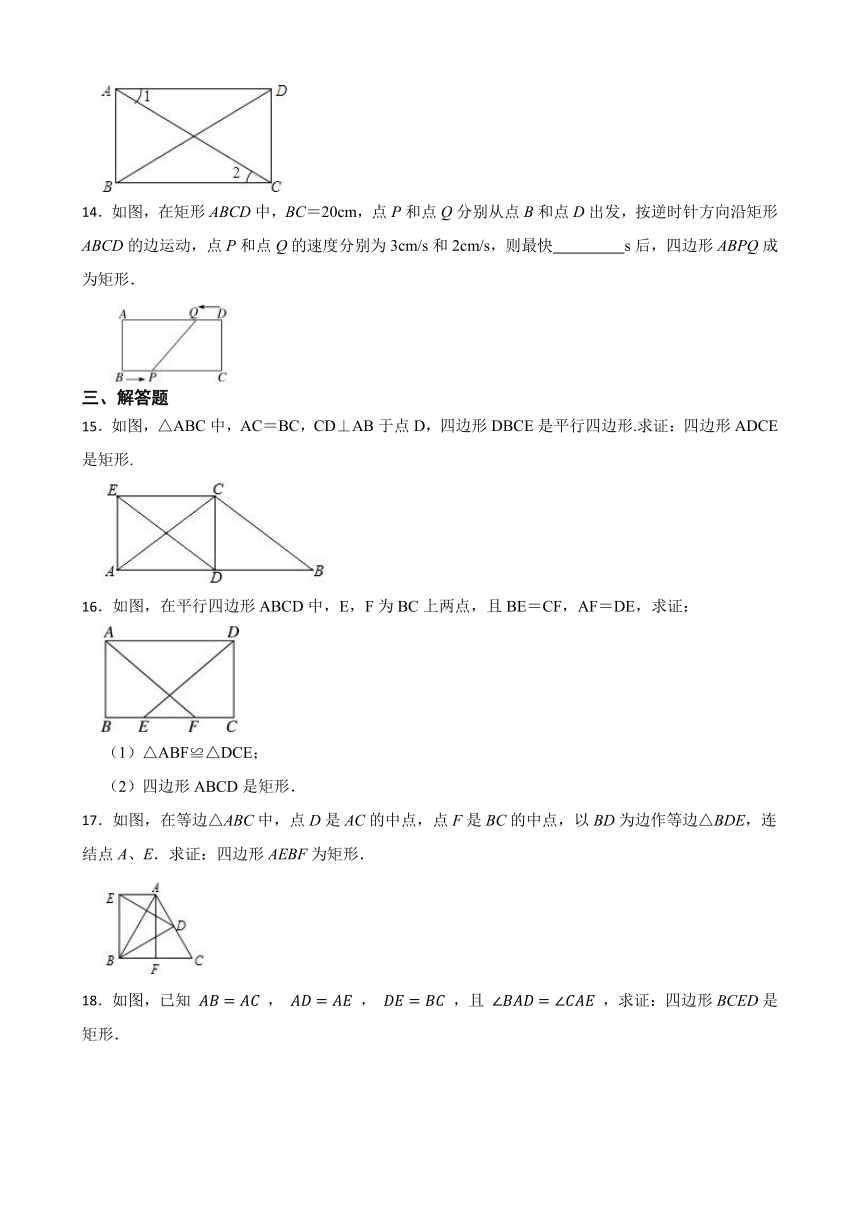
一、单选题
1.如图,下列条件中,能使平行四边形ABCD成为矩形的是( )
A.AB=BC B.AB=CD C.AC⊥BD D.AC=BD
2.如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是( )
A. B.AC,BD互相平分
C. D.
3.下列命题中,真命题是( )
A.对角线互相平分且相等的四边形是矩形
B.对角线互相垂直且相等的四边形是矩形
C.对角线互相平分的四边形是矩形
D.对角线互相垂直的四边形是矩形
4.在 ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO
C.AO⊥BO D.∠OBC=∠OBA
5.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD;则不能使四边形ABCD成为矩形的是( ).
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
6. ABCD添加下列条件后,仍不能使它成为矩形的是( )
A.AB⊥BC B.AC=BD C.∠A=∠B D.BC= CD
7.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量其内角是否均为直角 D.测量对角线是否垂直
8.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
9.己知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
10.如图,点P是Rt△ABC中斜边AC (不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )
A.1.5 B.2 C.4.8 D.2.4
二、填空题
11.杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面 .(填“合格”或“不合格”).
12.在四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是: .(不再添加线或字母,写出一种情况即可)
13.如图所示,已知平行四边形ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明平行四边形ABCD是矩形的有(填写序号) .
14.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
三、解答题
15.如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
16.如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE,求证:
(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
17.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连结点A、E.求证:四边形AEBF为矩形.
18.如图,已知 , , ,且 ,求证:四边形BCED是矩形.
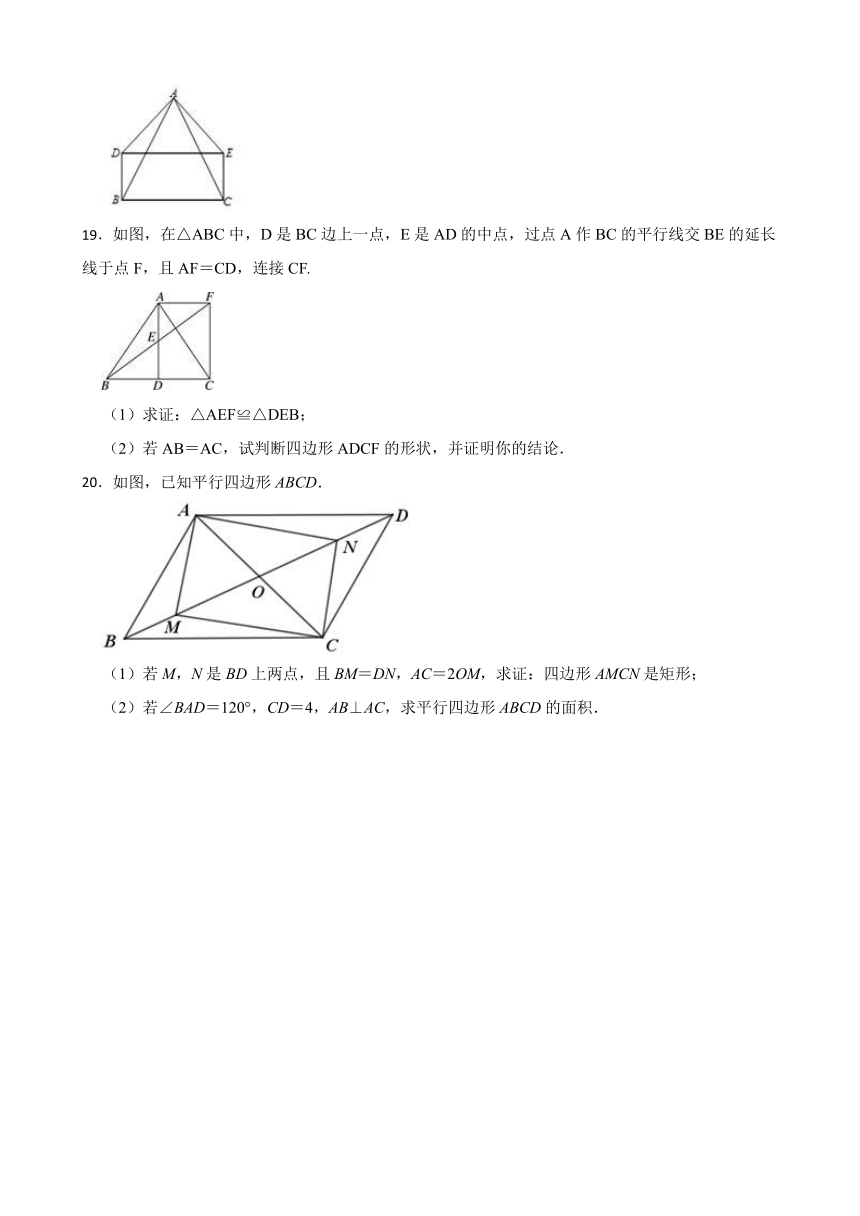
19.如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
20.如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】不合格
12.【答案】AD=BC(答案不唯一)
13.【答案】①④
14.【答案】4
15.【答案】证明:∵AC=BC,CD⊥AB,
∴∠ADC=90°,AD=BD.
∵在 DBCE中,EC∥BD,EC=BD,
∴EC∥AD,EC=AD.
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴四边形ADCE是矩形.
16.【答案】(1)证明:∵四边形ABCD为平行四边形
∴AB=CD
又∵BE=CF
∴BE+EF=CF+EF,
即BF=CE
又∵AF=DE
∴△ABF≌△DCE
(2)证明:∵四边形ABCD为平行四边形
∴AB∥CD
∵∠B=∠C
∴∠B=∠C=90°
∴平行四边形ABCD为矩形。
17.【答案】证明:∵在等边△ABC中,点D是AC的中点,点F是BC的中点,
∴AB = BC,∠ADB = ∠AFB= 90°,∠DBC=30°,
∠BAD = ∠ABF = 60°
∴△ABF≌△ABD,
∴BD = AF.
∵△BDE是等边三角形,
∴BD = BE,∠EBD = 60°.
∴AF = BE,∠EBF = ∠EBD + ∠DBC = 90°.
∴∠AFC = ∠EBF.
∴AF∥BE.
∴四边形AEBF是平行四边形.
∵∠EBF=90°,
∴平行四边形AEBF是矩形.
18.【答案】证明:连接BE、CD.
在△ABD和△ACE中
∵AB=AC,AD=AE,∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴BD=CE
∵DE=BC
∴四边形BCED为平行四边形
∵∠BAD=∠CAE
∴∠BAD+∠CAB=∠CAE+∠CAB
即∠CAD=∠BAE
在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠BAE
∴△ADC≌△AEB(SAS)
∴CD=BE
∴四边形BCED为矩形。
19.【答案】(1)证明:∵AF∥BC
∴∠AFE=∠DCE,∠FAE=∠CDE
∵点E为AD的中点
∴AE=DE
在△AEF和△DEC中,∵∠AFE=∠DCE,∠EAF=∠CDE,AE=DE
∴△AEF≌△DEC
(2)解:若AB=AC,∴四边形AFBD为矩形,理由如下:
∵AF∥BD,AF=BD
∴四边形AFBD是平行四边形
∵△AEF≌△DEC
∴AF=CD
∵AF=BD
∴CD=BD
∵AB=AC,BD=CD
∴∠ADB=90°
∴平行四边形AFBD为矩形。
20.【答案】(1)解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= AB=4 ,
∴平行四边形ABCD的面积=AC AB=4 4=16 .
一、单选题
1.如图,下列条件中,能使平行四边形ABCD成为矩形的是( )
A.AB=BC B.AB=CD C.AC⊥BD D.AC=BD
2.如图所示,四边形ABCD的对角线为AC,BD,且 ,则下列条件能判定四边形ABCD是矩形的是( )
A. B.AC,BD互相平分
C. D.
3.下列命题中,真命题是( )
A.对角线互相平分且相等的四边形是矩形
B.对角线互相垂直且相等的四边形是矩形
C.对角线互相平分的四边形是矩形
D.对角线互相垂直的四边形是矩形
4.在 ABCD中,AC与BD相交于点O,要使四边形ABCD是矩形,还需添加一个条件,这个条件可以是( )
A.AO=CO B.AO=BO
C.AO⊥BO D.∠OBC=∠OBA
5.如图,四边形ABCD的对角线AC、BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD;则不能使四边形ABCD成为矩形的是( ).
A.①②③ B.②③④ C.②⑤⑥ D.④⑤⑥
6. ABCD添加下列条件后,仍不能使它成为矩形的是( )
A.AB⊥BC B.AC=BD C.∠A=∠B D.BC= CD
7.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形.下面是某个合作小组的4位同学拟定的方案,其中正确的是( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量其内角是否均为直角 D.测量对角线是否垂直
8.在四边形ABCD中,AD∥BC,下列选项中,不能判定四边形ABCD为矩形的是( )
A.AD=BC且AC=BD B.AD=BC且∠A=∠B
C.AB=CD且∠A=∠C D.AB=CD且∠A=∠B
9.己知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )
A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC
10.如图,点P是Rt△ABC中斜边AC (不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )
A.1.5 B.2 C.4.8 D.2.4
二、填空题
11.杨师傅要做一个长方形的桌面,做好后量得长为2m,宽为1.5m,对角线为2.15m,则这个桌面 .(填“合格”或“不合格”).
12.在四边形ABCD中,AD∥BC,∠D=90°,如果再添加一个条件,可以得到四边形ABCD是矩形,那么可以添加的条件是: .(不再添加线或字母,写出一种情况即可)
13.如图所示,已知平行四边形ABCD,下列条件:①AC=BD,②AB=AD,③∠1=∠2,④AB⊥BC中,能说明平行四边形ABCD是矩形的有(填写序号) .
14.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
三、解答题
15.如图,△ABC中,AC=BC,CD⊥AB于点D,四边形DBCE是平行四边形.求证:四边形ADCE是矩形.
16.如图,在平行四边形ABCD中,E,F为BC上两点,且BE=CF,AF=DE,求证:
(1)△ABF≌△DCE;
(2)四边形ABCD是矩形.
17.如图,在等边△ABC中,点D是AC的中点,点F是BC的中点,以BD为边作等边△BDE,连结点A、E.求证:四边形AEBF为矩形.
18.如图,已知 , , ,且 ,求证:四边形BCED是矩形.
19.如图,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,且AF=CD,连接CF.
(1)求证:△AEF≌△DEB;
(2)若AB=AC,试判断四边形ADCF的形状,并证明你的结论.
20.如图,已知平行四边形ABCD.
(1)若M,N是BD上两点,且BM=DN,AC=2OM,求证:四边形AMCN是矩形;
(2)若∠BAD=120°,CD=4,AB⊥AC,求平行四边形ABCD的面积.
答案解析部分
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】不合格
12.【答案】AD=BC(答案不唯一)
13.【答案】①④
14.【答案】4
15.【答案】证明:∵AC=BC,CD⊥AB,
∴∠ADC=90°,AD=BD.
∵在 DBCE中,EC∥BD,EC=BD,
∴EC∥AD,EC=AD.
∴四边形ADCE是平行四边形.
又∵∠ADC=90°,
∴四边形ADCE是矩形.
16.【答案】(1)证明:∵四边形ABCD为平行四边形
∴AB=CD
又∵BE=CF
∴BE+EF=CF+EF,
即BF=CE
又∵AF=DE
∴△ABF≌△DCE
(2)证明:∵四边形ABCD为平行四边形
∴AB∥CD
∵∠B=∠C
∴∠B=∠C=90°
∴平行四边形ABCD为矩形。
17.【答案】证明:∵在等边△ABC中,点D是AC的中点,点F是BC的中点,
∴AB = BC,∠ADB = ∠AFB= 90°,∠DBC=30°,
∠BAD = ∠ABF = 60°
∴△ABF≌△ABD,
∴BD = AF.
∵△BDE是等边三角形,
∴BD = BE,∠EBD = 60°.
∴AF = BE,∠EBF = ∠EBD + ∠DBC = 90°.
∴∠AFC = ∠EBF.
∴AF∥BE.
∴四边形AEBF是平行四边形.
∵∠EBF=90°,
∴平行四边形AEBF是矩形.
18.【答案】证明:连接BE、CD.
在△ABD和△ACE中
∵AB=AC,AD=AE,∠BAD=∠CAE
∴△ABD≌△ACE(SAS)
∴BD=CE
∵DE=BC
∴四边形BCED为平行四边形
∵∠BAD=∠CAE
∴∠BAD+∠CAB=∠CAE+∠CAB
即∠CAD=∠BAE
在△ACD和△ABE中,
∵AC=AB,AD=AE,∠CAD=∠BAE
∴△ADC≌△AEB(SAS)
∴CD=BE
∴四边形BCED为矩形。
19.【答案】(1)证明:∵AF∥BC
∴∠AFE=∠DCE,∠FAE=∠CDE
∵点E为AD的中点
∴AE=DE
在△AEF和△DEC中,∵∠AFE=∠DCE,∠EAF=∠CDE,AE=DE
∴△AEF≌△DEC
(2)解:若AB=AC,∴四边形AFBD为矩形,理由如下:
∵AF∥BD,AF=BD
∴四边形AFBD是平行四边形
∵△AEF≌△DEC
∴AF=CD
∵AF=BD
∴CD=BD
∵AB=AC,BD=CD
∴∠ADB=90°
∴平行四边形AFBD为矩形。
20.【答案】(1)解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵对角线BD上的两点M、N满足BM=DN,
∴OB﹣BM=OD﹣DN,即OM=ON,
∴四边形AMCN是平行四边形,
∵AC=2OM,
∴MN=AC,
∴四边形AMCN是矩形;
(2)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=4,
∴∠BAD+∠ABC=180°,
∵∠BAD=120°,
∴∠ABC=60°,
∵AB⊥AC,
∴∠BAC=90°,
∴AC= AB=4 ,
∴平行四边形ABCD的面积=AC AB=4 4=16 .
