高中数学苏教版(2019 )选择性必修第二册 9.1.2 线性回归方程(学案+课时练 word版含解析)
文档属性
| 名称 | 高中数学苏教版(2019 )选择性必修第二册 9.1.2 线性回归方程(学案+课时练 word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 859.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 19:55:24 | ||
图片预览




文档简介
9.1.2 线性回归方程
学习目标 1.能结合实例,根据散点图,判断两个变量是否具有相关关系.2.了解最小二乘法原理,会求线性回归方程,并能根据线性回归方程进行预测.
导语
恩格尔系数(Engel’s Coefficient)是根据恩格尔定律得出的比例数,指居民家庭中食物支出占消费总支出的比重,是衡量生活水平高低的一个指标.其计算公式:恩格尔系数=食物支出金额÷总支出金额.
一个家庭收入越少,家庭收入中或者家庭总支出中用来购买食物的支出所占的比例就越大,随着家庭收入的增加,家庭收入中或者家庭支出中用来购买食物的支出所占比例将会下降.
恩格尔系数是预测生活水平高低的一个模型,那么当两个变量线性相关时,我们如何对样本数据建立一个模型进行预测?
一、线性回归模型
问题 如果散点图中的样本点大体分布在一条直线附近,怎样选择恰当的直线反映两个变量之间的线性相关关系?
提示 可以用y=a+bx+ε来反映两个变量之间的线性关系.
知识梳理
1.随机误差
具有线性相关关系的两个变量的取值x,y,y的值不能由x完全确定,它们之间是统计相关关系,可将x,y之间的关系表示为y=a+bx+ε,其中a+bx是确定性函数,ε称为随机误差.
2.随机误差产生的主要原因
(1)所用的确定性函数不恰当引起的误差;
(2)忽略了某些因素的影响;
(3)存在观测误差.
3.线性回归模型中a,b值的求法
y=a+bx+ε称为线性回归模型.
a,b的估计值为,,则
4.回归直线和线性回归方程
直线=+x称为回归直线,此直线方程即为线性回归方程,称为回归截距,称为回归系数,称为回归值.
注意点:
(1)线性回归方程的系数的计算,有时利用公式=;
(2)线性回归方程=x+必经过样本点的中心(,).
例1 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
求线性回归方程.
解 列出下表,并用科学计算器进行有关计算.
i 1 2 3 4 5
xi 2 4 5 6 8
yi 30 40 60 50 70
xiyi 60 160 300 300 560
x 4 16 25 36 64
=5,=50,=145,iyi=1 380
则===6.5,
=-=50-6.5×5=17.5.
故所求的线性回归方程是=6.5x+17.5.
反思感悟 求线性回归方程可分如下四步来完成
(1)列:列表表示xi,yi,x,xiyi.
(2)算:计算,,,iyi.
(3)代:代入公式计算,的值.
(4)写:写出线性回归方程.
跟踪训练1 某班5名学生的数学和物理成绩如表:
学生 学科 A B C D E
数学成绩(x) 88 76 73 66 63
物理成绩(y) 78 65 71 64 61
求物理成绩y对数学成绩x的线性回归方程.
解 =×(88+76+73+66+63)=73.2,
=×(78+65+71+64+61)=67.8.
iyi=88×78+76×65+73×71+66×64+63×61
=25 054.
=882+762+732+662+632=27 174.
所以==
≈0.625,
=-≈67.8-0.625×73.2=22.05.
所以所求线性回归方程是=0.625x+22.05.
二、利用线性回归方程对总体进行估计
例2 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得如表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程=x+;
(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式:=,=-.
解 (1)散点图如图所示.
(2)==9,==4,
=62+82+102+122=344,
iyi=6×2+8×3+10×5+12×6=158,
===0.7,
=-=4-0.7×9=-2.3,
故线性回归方程为=0.7x-2.3.
(3)由(2)中线性回归方程可知,当x=9时,=0.7×9-2.3=4,即预测记忆力为9的同学的判断力为4.
反思感悟 (1)判断两个变量是否线性相关:可以利用经验,也可以画散点图.
(2)求线性回归方程,注意运算的正确性.
(3)根据线性回归方程进行预测估计:估计值不是实际值,两者会有一定的误差.
跟踪训练2 假设关于某种设备的使用年限x(单位:年)与所支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
已知=90,≈140.8,iyi=112.3,≈8.9,≈1.4.
(1)计算y与x之间的相关系数(精确到0.001),并求出线性回归方程;
(2)根据线性回归方程,预测假设使用年限为10年时,维修费用约是多少万元?
解 (1)∵==4,
==5.
iyi-5=112.3-5×4×5=12.3,
-52=90-5×42=10,
-52=140.8-125=15.8,
所以r===≈
≈0.987.
又===1.23.
=-=5-1.23×4=0.08.
所以线性回归方程为=1.23x+0.08.
(2)当x=10时,=1.23×10+0.08=12.38(万元),
即假设使用10年时,维修费用约为12.38万元.
三、非线性回归问题
知识梳理
解非线性回归分析问题的一般步骤
有些非线性回归分析问题并不给出函数,这时我们可以根据已知数据画出散点图,与学过的各种函数(幂函数、指数函数、对数函数等)的图象进行比较,挑选一种跟这些散点拟合得最好的函数,用适当的变量进行变换,把问题转化为线性回归分析问题,使之得到解决.
一般步骤为:
说明:由于涉及的数据比较多,考虑到可操作性,考试时往往会给出散点图,或将画散点图这一步骤省略,只需要选一些数据,画一下草图,作出判断即可,并且相关数据都会直接给出.
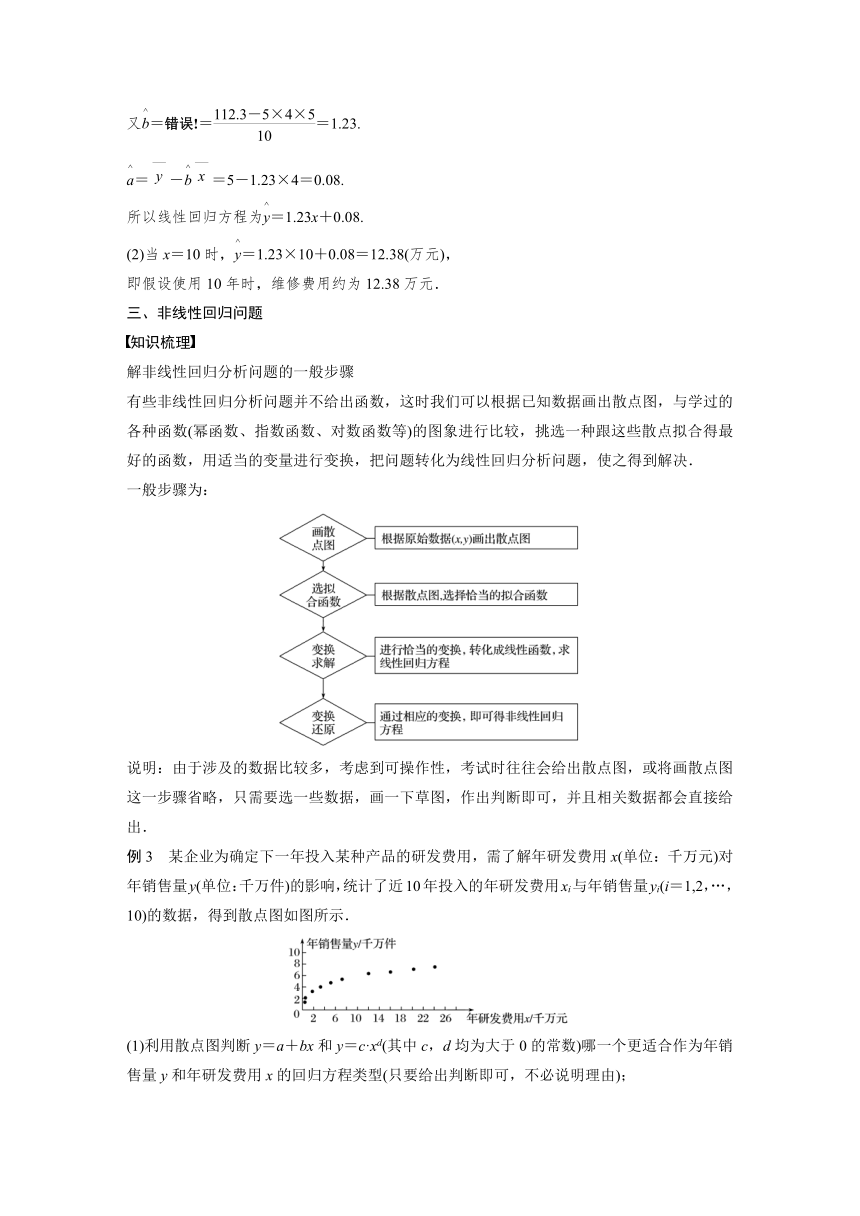
例3 某企业为确定下一年投入某种产品的研发费用,需了解年研发费用x(单位:千万元)对年销售量y(单位:千万件)的影响,统计了近10年投入的年研发费用xi与年销售量yi(i=1,2,…,10)的数据,得到散点图如图所示.
(1)利用散点图判断y=a+bx和y=c·xd(其中c,d均为大于0的常数)哪一个更适合作为年销售量y和年研发费用x的回归方程类型(只要给出判断即可,不必说明理由);
(2)对数据作出如下处理,令μ1=ln xi,vi=ln yi,得到相关统计量的值如下表:
i i (ui-)(vi-) (ui-)2
15 15 28.25 56.5
根据第(1)问的判断结果及表中数据,求y关于x的回归方程.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=-.
解 (1)由散点图可知,选择回归类型y=c·xd更适合.
(2)对y=c·xd两边取对数,得ln y=ln c+dln x,
即v=ln c+du.
由表中数据求得====,
===.
令ln c=m,则=-=-×=,
即c=.所以年销售量y与年研发费用x的回归方程为y=
反思感悟 非线性回归问题的处理方法
(1)指数函数型y=ebx+a
①函数y=ebx+a的图象,如图所示.
②处理方法:两边取对数得ln y=ln ebx+a,即ln y=bx+a.令z=ln y,把原始数据(x,y)转化为(x,z),再根据线性回归模型的方法求出a,b.
(2)对数函数型y=bln x+a
①函数y=bln x+a的图象,如图所示.
②处理方法:设x′=ln x,原方程可化为y=bx′+a,
再根据线性回归模型的方法求出a,b.
(3)y=bx2+a型
处理方法:设x′=x2,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.
跟踪训练3 某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据:
x 1 2 3 4 5 6 7 8
y 112 61 44.5 35 30.5 28 25 24
根据以上数据,绘制了散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型y=a+和指数函数模型y=cedx分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为=96.54e-0.2x,ln y与x的相关系数r1=-0.94.
参考数据:
iyi 2 i e-2
183.4 0.34 0.115 1.53 360 22 385.5 61.4 0.135
(1)用反比例函数模型求y关于x的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为:=,=-,
相关系数r=
解 (1)令u=,
则y=a+可转化为y=a+bu,
因为==45,
所以=
===100,
则=-=45-100×0.34=11,
所以=11+100u,
所以y关于x的回归方程为=11+.
(2)y与的相关系数为
r2=
=≈0.99.
因为|r1|<|r2|,所以用反比例函数模型拟合效果更好,
当x=10时,y=+11=21(元),
所以当产量为10千件时,每件产品的非原料成本为21元.
(3)①当产品单价为100元,设订单数为m千件,因为签订9千件订单的概率为0.8,签订10千件订单的概率为0.2,
所以E(m)=9×0.8+10×0.2=9.2,
所以企业利润为
100×9.2-9.2×=626.8(千元).
②当产品单价为90元,设订单数为n千件,
因为签订10千件订单的概率为0.3,签订11千件订单的概率为0.7,
所以E(n)=10×0.3+11×0.7=10.7,
所以企业利润为
90×10.7-10.7×=638.3(千元).
故企业要想获得更高利润,产品单价应选择90元.
1.知识清单:
(1)线性回归模型.
(2)利用线性回归方程对总体进行估计.
(3)非线性回归问题.
2.方法归纳:最小二乘法、转化化归、公式法.
3.常见误区:不判断变量间是否具有线性相关关系,盲目求解线性回归方程致误.
1.(多选)以下四个散点图中,两个变量的关系适合用线性回归模型刻画的是( )
答案 AC
解析 AC中的点分布在一条直线附近,适合用线性回归模型刻画.
2.已知人的年龄x与人体脂肪含量的百分数y的线性回归方程为=0.577x-0.448,如果某人36岁,那么这个人的脂肪含量( )
A.一定是20.3%
B.在20.3%附近的可能性比较大
C.无任何参考数据
D.以上解释都无道理
答案 B
解析 将x=36代入线性回归方程得=0.577×36-0.448≈20.3,故这个人的脂肪含量在20.3%附近的可能性较大,故选B.
3.已知具有线性关系的两个变量x,y之间的一组数据如下,且线性回归方程是=0.95x+,则当x=6时,y的预测值为( )
x 0 1 2 3 4
y 2.2 4.3 4.5 4.8 6.7
A.8.4 B.8.3 C.8.2 D.8.1
答案 B
解析 由已知数据可得=2,=4.5,
∴4.5=0.95×2+,∴=2.6,
∴线性回归方程是=0.95x+2.6,
当x=6时,y的预测值为0.95×6+2.6=8.3.
4.在研究两个变量的相关关系时,观察散点图发现样本点集中于某一条指数曲线y=ebx+a的周围.令=ln y,求得线性回归方程为=0.25x-2.58,则该模型的非线性回归方程为________.
答案 =e0.25x-2.58
解析 因为=0.25x-2.58,=ln y,所以=e0.25x-2.58.
课时对点练
1.已知变量x,y之间具有线性关系,其散点图如图所示,则其线性回归方程可能为( )
A.=1.5x+2 B.=-1.5x+2
C.=1.5x-2 D.=-1.5x-2
答案 B
2.已知线性回归方程为=x+,其中=3且样本点的中心为(1,2),则线性回归方程为( )
A.=x+3 B.=-2x+3
C.=-x+3 D.=x-3
答案 C
解析 回归直线一定过样本点的中心.
3.某医学科研所对人体脂肪含量与年龄这两个变量研究得到一组随机样本数据,运用Excel软件计算得y=0.577x-0.448(x为人的年龄,y为人体脂肪含量).对年龄为37岁的人来说,下面说法正确的是( )
A.年龄为37岁的人体内脂肪含量一定为20.90
B.年龄为37岁的人体内脂肪含量约为21.01
C.年龄为37岁的人群中的体内脂肪含量平均为20.90
D.年龄为37岁的人群中的大部分人的体内脂肪含量约为31.5
答案 C
解析 当x=37时,=0.577×37-0.448=20.901≈20.90,由此估计,年龄为37岁的人群中的体内脂肪含量平均为20.90.
4.已知变量x和y满足关系y=-0.1x+1,变量y与z正相关.下列结论中正确的是( )
A.x与y正相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y负相关,x与z负相关
D.x与y负相关,x与z正相关
答案 C
解析 因为y=-0.1x+1,-0.1<0,所以x与y负相关.又y与z正相关,故可设z=ay+b(a>0),所以z=-0.1ax+a+b,-0.1a<0.所以x与z负相关.
5.(多选)对于线性回归方程=x+ (>0),下列说法正确的是( )
A.当x增加一个单位时,的值平均增加个单位
B.点(,)一定在=x+所表示的直线上
C.当x=t时,一定有=t+
D.当x=t时,y的值近似为t+
答案 ABD
解析 线性回归方程是一个模拟函数,它表示的是一系列离散的点大致所在直线的位置及其大致变化规律,所以有些散点不一定在回归直线上.
6.(多选)已知在最小二乘法原理下,具有相关关系的变量x,y之间的线性回归方程为=
-0.7x+10.3,且变量x,y之间的相关数据如表所示,则下列说法错误的是( )
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间呈正相关关系
B.可以预测,当x=20时,=3.7
C.可求得表中m=4.7
D.由表格数据知,该回归直线必过点(9,4)
答案 ABC
解析 由x与y的线性回归方程可知,
回归系数为-0.7,且-0.7<0,
∴变量x,y之间呈负相关关系,故A错误;
当x=20时,=-0.7×20+10.3=-3.7,故B错误;
由表中数据可知=9,==,
由点(,)必在回归直线上,
得=-0.7×9+10.3,
解得m=5,故C错误;
∵m=5,∴==4,
∴回归直线必过点(9,4),故D正确.
7.若线性回归方程中的回归系数=0,则相关系数r=________.
答案 0
解析 相关系数r=与=的分子相同,故r=0.
8.由变量x与y相对应的一组样本数据(1,y1),(5,y2),(7,y3),(13,y4),(19,y5)得到的线性回归方程为=2x+45,则=________.
答案 63
解析 ∵=(1+5+7+13+19)=9,=2+45,
∴=2×9+45=63.
9.某地区2013年至2019年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年份 2013 2014 2015 2016 2017 2018 2019
年份代号t 1 2 3 4 5 6 7
人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
(1)求y关于t的线性回归方程;
(2)利用(1)中的线性回归方程,分析2013年至2019年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2021年农村居民家庭人均纯收入.
附:线性回归直线的斜率和截距的最小二乘估计公式分别为=,=-,
参考数据:(ti-)2=28,(ti-)(yi-)=14.
解 (1)由所给数据计算得
=(1+2+3+4+5+6+7)=4,
=(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
===0.5,
=-=4.3-0.5×4=2.3,
所求线性回归方程为=0.5t+2.3.
(2)由(1)知,=0.5>0,故2013年至2019年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2021年的年份代号t=9代入(1)中的线性回归方程,得=0.5×9+2.3=6.8,
故预测该地区2021年农村居民家庭人均纯收入为6.8千元.
10.根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
(1)依据数据的散点图可以看出,可用线性回归模型拟合y与x的关系,请计算相关系数r并加以说明(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合);
(2)求y关于x的线性回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量y约为多少?
附:相关系数公式r=,参考数据:(xi-)(yi-)=6,(xi-)2=20,(yi-)2=2,≈0.95.
回归直线=x+中斜率和截距的最小二乘估计公式分别为=,=-.
解 (1)相关系数r=
==≈0.95.
因为|r|>0.75,所以可用线性回归模型拟合y与x的关系.
(2)由已知数据可得==5,
==4.===0.3.
那么=4-5×0.3=2.5.
所以线性回归方程为=0.3x+2.5.当x=12时,=0.3×12+2.5=6.1,即当液体肥料每亩使用量为12千克时,西红柿亩产量的增加量约为6.1百千克.
11.已知变量x与y负相关,且由观测数据求得样本平均数=3,=3.5,则由该观测数据求得的线性回归方程可能是( )
A.=-2x+9.5 B.=2x-2.4
C.=-0.3x-4.4 D.=0.4x+2.3
答案 A
解析 因为变量x与y负相关,所以排除B,D,将样本平均数=3,=3.5代入选项验证可知,选项A符合题意.
12.某校小卖部为了了解奶茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的奶茶杯数与当天的气温,得到下表中的数据,并根据该样本数据用最小二乘法建立了线性回归方程=-2x+60,则样本数据中污损的数据y0应为( )
气温x(℃) -1 13 10 18
杯数y y0 34 38 24
A.58 B.64 C.62 D.60
答案 B
解析 由表中数据易知=10,代入=-2x+60中,
得=40.由=40,得y0=64.
13.(多选)根据如下样本数据得到的线性回归方程为=x+,则( )
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
A.>0 B.>0 C.<0 D.<0
答案 AD
解析 作出散点图如下:
观察图象可知,线性回归方程=x+的斜率<0,
当x=0时,=>0.故>0,<0.
14.已知y与x之间具有很强的线性相关关系,现观测得到x,y的四组观测值并制作了对照表.
x 15 17 11 -3
y 6 17 21 36
由表中数据粗略地得到线性回归方程为=x+60,其中的值没有写上,当x不小于-5时,预测y最大为________.(结果保留整十数)
答案 80
解析 由表格可知=10,=20,代入线性回归方程可知=-4,令x≥-5,可得≤80.故预测y的最大值为80.
15.已知变量y关于x的非线性回归方程为=,其一组数据如下表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
答案 D
解析 将式子两边取对数,得到ln =x-0.5,
令z=ln ,得到z=x-0.5,
列出x,z的取值对应的表格如下:
x 1 2 3 4
z 1 3 4 6
则==2.5,==3.5,
∵(,)满足z=x-0.5,
∴3.5=×2.5-0.5,解得=1.6,
∴z=1.6x-0.5,∴=e1.6x-0.5,
当x=5时,=e1.6×5-0.5=.
16.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) 8 8.2 8.4 8.6 8.8 9
销量y(件) 90 84 83 80 75 68
(1)求线性回归方程=x+,其中=-20;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
解 (1)由于=×(8+8.2+8.4+8.6+8.8+9)=8.5,
=×(90+84+83+80+75+68)=80.
所以=-=80+20×8.5=250,
从而线性回归方程为=-20x+250.
(2)设工厂获得的利润为L元,依题意得L=x(-20x+250)-4(-20x+250)=-20x2+330x-
1 000=-20(x-8.25)2+361.25.
故当单价定为8.25元时,工厂可获得最大利润.
学习目标 1.能结合实例,根据散点图,判断两个变量是否具有相关关系.2.了解最小二乘法原理,会求线性回归方程,并能根据线性回归方程进行预测.
导语
恩格尔系数(Engel’s Coefficient)是根据恩格尔定律得出的比例数,指居民家庭中食物支出占消费总支出的比重,是衡量生活水平高低的一个指标.其计算公式:恩格尔系数=食物支出金额÷总支出金额.
一个家庭收入越少,家庭收入中或者家庭总支出中用来购买食物的支出所占的比例就越大,随着家庭收入的增加,家庭收入中或者家庭支出中用来购买食物的支出所占比例将会下降.
恩格尔系数是预测生活水平高低的一个模型,那么当两个变量线性相关时,我们如何对样本数据建立一个模型进行预测?
一、线性回归模型
问题 如果散点图中的样本点大体分布在一条直线附近,怎样选择恰当的直线反映两个变量之间的线性相关关系?
提示 可以用y=a+bx+ε来反映两个变量之间的线性关系.
知识梳理
1.随机误差
具有线性相关关系的两个变量的取值x,y,y的值不能由x完全确定,它们之间是统计相关关系,可将x,y之间的关系表示为y=a+bx+ε,其中a+bx是确定性函数,ε称为随机误差.
2.随机误差产生的主要原因
(1)所用的确定性函数不恰当引起的误差;
(2)忽略了某些因素的影响;
(3)存在观测误差.
3.线性回归模型中a,b值的求法
y=a+bx+ε称为线性回归模型.
a,b的估计值为,,则
4.回归直线和线性回归方程
直线=+x称为回归直线,此直线方程即为线性回归方程,称为回归截距,称为回归系数,称为回归值.
注意点:
(1)线性回归方程的系数的计算,有时利用公式=;
(2)线性回归方程=x+必经过样本点的中心(,).
例1 某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
x 2 4 5 6 8
y 30 40 60 50 70
求线性回归方程.
解 列出下表,并用科学计算器进行有关计算.
i 1 2 3 4 5
xi 2 4 5 6 8
yi 30 40 60 50 70
xiyi 60 160 300 300 560
x 4 16 25 36 64
=5,=50,=145,iyi=1 380
则===6.5,
=-=50-6.5×5=17.5.
故所求的线性回归方程是=6.5x+17.5.
反思感悟 求线性回归方程可分如下四步来完成
(1)列:列表表示xi,yi,x,xiyi.
(2)算:计算,,,iyi.
(3)代:代入公式计算,的值.
(4)写:写出线性回归方程.
跟踪训练1 某班5名学生的数学和物理成绩如表:
学生 学科 A B C D E
数学成绩(x) 88 76 73 66 63
物理成绩(y) 78 65 71 64 61
求物理成绩y对数学成绩x的线性回归方程.
解 =×(88+76+73+66+63)=73.2,
=×(78+65+71+64+61)=67.8.
iyi=88×78+76×65+73×71+66×64+63×61
=25 054.
=882+762+732+662+632=27 174.
所以==
≈0.625,
=-≈67.8-0.625×73.2=22.05.
所以所求线性回归方程是=0.625x+22.05.
二、利用线性回归方程对总体进行估计
例2 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得如表数据:
x 6 8 10 12
y 2 3 5 6
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程=x+;
(3)试根据求出的线性回归方程,预测记忆力为9的同学的判断力.
参考公式:=,=-.
解 (1)散点图如图所示.
(2)==9,==4,
=62+82+102+122=344,
iyi=6×2+8×3+10×5+12×6=158,
===0.7,
=-=4-0.7×9=-2.3,
故线性回归方程为=0.7x-2.3.
(3)由(2)中线性回归方程可知,当x=9时,=0.7×9-2.3=4,即预测记忆力为9的同学的判断力为4.
反思感悟 (1)判断两个变量是否线性相关:可以利用经验,也可以画散点图.
(2)求线性回归方程,注意运算的正确性.
(3)根据线性回归方程进行预测估计:估计值不是实际值,两者会有一定的误差.
跟踪训练2 假设关于某种设备的使用年限x(单位:年)与所支出的维修费用y(单位:万元)有如下统计资料:
x 2 3 4 5 6
y 2.2 3.8 5.5 6.5 7.0
已知=90,≈140.8,iyi=112.3,≈8.9,≈1.4.
(1)计算y与x之间的相关系数(精确到0.001),并求出线性回归方程;
(2)根据线性回归方程,预测假设使用年限为10年时,维修费用约是多少万元?
解 (1)∵==4,
==5.
iyi-5=112.3-5×4×5=12.3,
-52=90-5×42=10,
-52=140.8-125=15.8,
所以r===≈
≈0.987.
又===1.23.
=-=5-1.23×4=0.08.
所以线性回归方程为=1.23x+0.08.
(2)当x=10时,=1.23×10+0.08=12.38(万元),
即假设使用10年时,维修费用约为12.38万元.
三、非线性回归问题
知识梳理
解非线性回归分析问题的一般步骤
有些非线性回归分析问题并不给出函数,这时我们可以根据已知数据画出散点图,与学过的各种函数(幂函数、指数函数、对数函数等)的图象进行比较,挑选一种跟这些散点拟合得最好的函数,用适当的变量进行变换,把问题转化为线性回归分析问题,使之得到解决.
一般步骤为:
说明:由于涉及的数据比较多,考虑到可操作性,考试时往往会给出散点图,或将画散点图这一步骤省略,只需要选一些数据,画一下草图,作出判断即可,并且相关数据都会直接给出.
例3 某企业为确定下一年投入某种产品的研发费用,需了解年研发费用x(单位:千万元)对年销售量y(单位:千万件)的影响,统计了近10年投入的年研发费用xi与年销售量yi(i=1,2,…,10)的数据,得到散点图如图所示.
(1)利用散点图判断y=a+bx和y=c·xd(其中c,d均为大于0的常数)哪一个更适合作为年销售量y和年研发费用x的回归方程类型(只要给出判断即可,不必说明理由);
(2)对数据作出如下处理,令μ1=ln xi,vi=ln yi,得到相关统计量的值如下表:
i i (ui-)(vi-) (ui-)2
15 15 28.25 56.5
根据第(1)问的判断结果及表中数据,求y关于x的回归方程.
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为=,=-.
解 (1)由散点图可知,选择回归类型y=c·xd更适合.
(2)对y=c·xd两边取对数,得ln y=ln c+dln x,
即v=ln c+du.
由表中数据求得====,
===.
令ln c=m,则=-=-×=,
即c=.所以年销售量y与年研发费用x的回归方程为y=
反思感悟 非线性回归问题的处理方法
(1)指数函数型y=ebx+a
①函数y=ebx+a的图象,如图所示.
②处理方法:两边取对数得ln y=ln ebx+a,即ln y=bx+a.令z=ln y,把原始数据(x,y)转化为(x,z),再根据线性回归模型的方法求出a,b.
(2)对数函数型y=bln x+a
①函数y=bln x+a的图象,如图所示.
②处理方法:设x′=ln x,原方程可化为y=bx′+a,
再根据线性回归模型的方法求出a,b.
(3)y=bx2+a型
处理方法:设x′=x2,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.
跟踪训练3 某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本y(元)与生产该产品的数量x(千件)有关,经统计得到如下数据:
x 1 2 3 4 5 6 7 8
y 112 61 44.5 35 30.5 28 25 24
根据以上数据,绘制了散点图.
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型y=a+和指数函数模型y=cedx分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为=96.54e-0.2x,ln y与x的相关系数r1=-0.94.
参考数据:
iyi 2 i e-2
183.4 0.34 0.115 1.53 360 22 385.5 61.4 0.135
(1)用反比例函数模型求y关于x的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线=+u的斜率和截距的最小二乘估计分别为:=,=-,
相关系数r=
解 (1)令u=,
则y=a+可转化为y=a+bu,
因为==45,
所以=
===100,
则=-=45-100×0.34=11,
所以=11+100u,
所以y关于x的回归方程为=11+.
(2)y与的相关系数为
r2=
=≈0.99.
因为|r1|<|r2|,所以用反比例函数模型拟合效果更好,
当x=10时,y=+11=21(元),
所以当产量为10千件时,每件产品的非原料成本为21元.
(3)①当产品单价为100元,设订单数为m千件,因为签订9千件订单的概率为0.8,签订10千件订单的概率为0.2,
所以E(m)=9×0.8+10×0.2=9.2,
所以企业利润为
100×9.2-9.2×=626.8(千元).
②当产品单价为90元,设订单数为n千件,
因为签订10千件订单的概率为0.3,签订11千件订单的概率为0.7,
所以E(n)=10×0.3+11×0.7=10.7,
所以企业利润为
90×10.7-10.7×=638.3(千元).
故企业要想获得更高利润,产品单价应选择90元.
1.知识清单:
(1)线性回归模型.
(2)利用线性回归方程对总体进行估计.
(3)非线性回归问题.
2.方法归纳:最小二乘法、转化化归、公式法.
3.常见误区:不判断变量间是否具有线性相关关系,盲目求解线性回归方程致误.
1.(多选)以下四个散点图中,两个变量的关系适合用线性回归模型刻画的是( )
答案 AC
解析 AC中的点分布在一条直线附近,适合用线性回归模型刻画.
2.已知人的年龄x与人体脂肪含量的百分数y的线性回归方程为=0.577x-0.448,如果某人36岁,那么这个人的脂肪含量( )
A.一定是20.3%
B.在20.3%附近的可能性比较大
C.无任何参考数据
D.以上解释都无道理
答案 B
解析 将x=36代入线性回归方程得=0.577×36-0.448≈20.3,故这个人的脂肪含量在20.3%附近的可能性较大,故选B.
3.已知具有线性关系的两个变量x,y之间的一组数据如下,且线性回归方程是=0.95x+,则当x=6时,y的预测值为( )
x 0 1 2 3 4
y 2.2 4.3 4.5 4.8 6.7
A.8.4 B.8.3 C.8.2 D.8.1
答案 B
解析 由已知数据可得=2,=4.5,
∴4.5=0.95×2+,∴=2.6,
∴线性回归方程是=0.95x+2.6,
当x=6时,y的预测值为0.95×6+2.6=8.3.
4.在研究两个变量的相关关系时,观察散点图发现样本点集中于某一条指数曲线y=ebx+a的周围.令=ln y,求得线性回归方程为=0.25x-2.58,则该模型的非线性回归方程为________.
答案 =e0.25x-2.58
解析 因为=0.25x-2.58,=ln y,所以=e0.25x-2.58.
课时对点练
1.已知变量x,y之间具有线性关系,其散点图如图所示,则其线性回归方程可能为( )
A.=1.5x+2 B.=-1.5x+2
C.=1.5x-2 D.=-1.5x-2
答案 B
2.已知线性回归方程为=x+,其中=3且样本点的中心为(1,2),则线性回归方程为( )
A.=x+3 B.=-2x+3
C.=-x+3 D.=x-3
答案 C
解析 回归直线一定过样本点的中心.
3.某医学科研所对人体脂肪含量与年龄这两个变量研究得到一组随机样本数据,运用Excel软件计算得y=0.577x-0.448(x为人的年龄,y为人体脂肪含量).对年龄为37岁的人来说,下面说法正确的是( )
A.年龄为37岁的人体内脂肪含量一定为20.90
B.年龄为37岁的人体内脂肪含量约为21.01
C.年龄为37岁的人群中的体内脂肪含量平均为20.90
D.年龄为37岁的人群中的大部分人的体内脂肪含量约为31.5
答案 C
解析 当x=37时,=0.577×37-0.448=20.901≈20.90,由此估计,年龄为37岁的人群中的体内脂肪含量平均为20.90.
4.已知变量x和y满足关系y=-0.1x+1,变量y与z正相关.下列结论中正确的是( )
A.x与y正相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y负相关,x与z负相关
D.x与y负相关,x与z正相关
答案 C
解析 因为y=-0.1x+1,-0.1<0,所以x与y负相关.又y与z正相关,故可设z=ay+b(a>0),所以z=-0.1ax+a+b,-0.1a<0.所以x与z负相关.
5.(多选)对于线性回归方程=x+ (>0),下列说法正确的是( )
A.当x增加一个单位时,的值平均增加个单位
B.点(,)一定在=x+所表示的直线上
C.当x=t时,一定有=t+
D.当x=t时,y的值近似为t+
答案 ABD
解析 线性回归方程是一个模拟函数,它表示的是一系列离散的点大致所在直线的位置及其大致变化规律,所以有些散点不一定在回归直线上.
6.(多选)已知在最小二乘法原理下,具有相关关系的变量x,y之间的线性回归方程为=
-0.7x+10.3,且变量x,y之间的相关数据如表所示,则下列说法错误的是( )
x 6 8 10 12
y 6 m 3 2
A.变量x,y之间呈正相关关系
B.可以预测,当x=20时,=3.7
C.可求得表中m=4.7
D.由表格数据知,该回归直线必过点(9,4)
答案 ABC
解析 由x与y的线性回归方程可知,
回归系数为-0.7,且-0.7<0,
∴变量x,y之间呈负相关关系,故A错误;
当x=20时,=-0.7×20+10.3=-3.7,故B错误;
由表中数据可知=9,==,
由点(,)必在回归直线上,
得=-0.7×9+10.3,
解得m=5,故C错误;
∵m=5,∴==4,
∴回归直线必过点(9,4),故D正确.
7.若线性回归方程中的回归系数=0,则相关系数r=________.
答案 0
解析 相关系数r=与=的分子相同,故r=0.
8.由变量x与y相对应的一组样本数据(1,y1),(5,y2),(7,y3),(13,y4),(19,y5)得到的线性回归方程为=2x+45,则=________.
答案 63
解析 ∵=(1+5+7+13+19)=9,=2+45,
∴=2×9+45=63.
9.某地区2013年至2019年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年份 2013 2014 2015 2016 2017 2018 2019
年份代号t 1 2 3 4 5 6 7
人均纯收入y 2.9 3.3 3.6 4.4 4.8 5.2 5.9
(1)求y关于t的线性回归方程;
(2)利用(1)中的线性回归方程,分析2013年至2019年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2021年农村居民家庭人均纯收入.
附:线性回归直线的斜率和截距的最小二乘估计公式分别为=,=-,
参考数据:(ti-)2=28,(ti-)(yi-)=14.
解 (1)由所给数据计算得
=(1+2+3+4+5+6+7)=4,
=(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
===0.5,
=-=4.3-0.5×4=2.3,
所求线性回归方程为=0.5t+2.3.
(2)由(1)知,=0.5>0,故2013年至2019年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元.
将2021年的年份代号t=9代入(1)中的线性回归方程,得=0.5×9+2.3=6.8,
故预测该地区2021年农村居民家庭人均纯收入为6.8千元.
10.根据统计,某蔬菜基地西红柿亩产量的增加量y(百千克)与某种液体肥料每亩使用量x(千克)之间的对应数据的散点图如图所示.
(1)依据数据的散点图可以看出,可用线性回归模型拟合y与x的关系,请计算相关系数r并加以说明(若|r|>0.75,则线性相关程度很高,可用线性回归模型拟合);
(2)求y关于x的线性回归方程,并预测液体肥料每亩使用量为12千克时,西红柿亩产量的增加量y约为多少?
附:相关系数公式r=,参考数据:(xi-)(yi-)=6,(xi-)2=20,(yi-)2=2,≈0.95.
回归直线=x+中斜率和截距的最小二乘估计公式分别为=,=-.
解 (1)相关系数r=
==≈0.95.
因为|r|>0.75,所以可用线性回归模型拟合y与x的关系.
(2)由已知数据可得==5,
==4.===0.3.
那么=4-5×0.3=2.5.
所以线性回归方程为=0.3x+2.5.当x=12时,=0.3×12+2.5=6.1,即当液体肥料每亩使用量为12千克时,西红柿亩产量的增加量约为6.1百千克.
11.已知变量x与y负相关,且由观测数据求得样本平均数=3,=3.5,则由该观测数据求得的线性回归方程可能是( )
A.=-2x+9.5 B.=2x-2.4
C.=-0.3x-4.4 D.=0.4x+2.3
答案 A
解析 因为变量x与y负相关,所以排除B,D,将样本平均数=3,=3.5代入选项验证可知,选项A符合题意.
12.某校小卖部为了了解奶茶销售量y(杯)与气温x(℃)之间的关系,随机统计了某4天卖出的奶茶杯数与当天的气温,得到下表中的数据,并根据该样本数据用最小二乘法建立了线性回归方程=-2x+60,则样本数据中污损的数据y0应为( )
气温x(℃) -1 13 10 18
杯数y y0 34 38 24
A.58 B.64 C.62 D.60
答案 B
解析 由表中数据易知=10,代入=-2x+60中,
得=40.由=40,得y0=64.
13.(多选)根据如下样本数据得到的线性回归方程为=x+,则( )
x 3 4 5 6 7 8
y 4.0 2.5 -0.5 0.5 -2.0 -3.0
A.>0 B.>0 C.<0 D.<0
答案 AD
解析 作出散点图如下:
观察图象可知,线性回归方程=x+的斜率<0,
当x=0时,=>0.故>0,<0.
14.已知y与x之间具有很强的线性相关关系,现观测得到x,y的四组观测值并制作了对照表.
x 15 17 11 -3
y 6 17 21 36
由表中数据粗略地得到线性回归方程为=x+60,其中的值没有写上,当x不小于-5时,预测y最大为________.(结果保留整十数)
答案 80
解析 由表格可知=10,=20,代入线性回归方程可知=-4,令x≥-5,可得≤80.故预测y的最大值为80.
15.已知变量y关于x的非线性回归方程为=,其一组数据如下表所示:
x 1 2 3 4
y e e3 e4 e6
若x=5,则预测y的值可能为( )
A.e5 B. C.e7 D.
答案 D
解析 将式子两边取对数,得到ln =x-0.5,
令z=ln ,得到z=x-0.5,
列出x,z的取值对应的表格如下:
x 1 2 3 4
z 1 3 4 6
则==2.5,==3.5,
∵(,)满足z=x-0.5,
∴3.5=×2.5-0.5,解得=1.6,
∴z=1.6x-0.5,∴=e1.6x-0.5,
当x=5时,=e1.6×5-0.5=.
16.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) 8 8.2 8.4 8.6 8.8 9
销量y(件) 90 84 83 80 75 68
(1)求线性回归方程=x+,其中=-20;
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)
解 (1)由于=×(8+8.2+8.4+8.6+8.8+9)=8.5,
=×(90+84+83+80+75+68)=80.
所以=-=80+20×8.5=250,
从而线性回归方程为=-20x+250.
(2)设工厂获得的利润为L元,依题意得L=x(-20x+250)-4(-20x+250)=-20x2+330x-
1 000=-20(x-8.25)2+361.25.
故当单价定为8.25元时,工厂可获得最大利润.
