北师大版七年级数学下册 4.3 等腰三角形性质 课件(共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 4.3 等腰三角形性质 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 09:52:26 | ||
图片预览






文档简介
(共23张PPT)
简单的轴对称图形(2)
——等腰三角形
1.什么叫轴对称图形?
2.线段是轴对称图形吗?
它的对称轴是什么?
3.角是轴对称图形吗?
它的对称轴是什么?
温故知新
简单的轴对称图形(2)
——等腰三角形
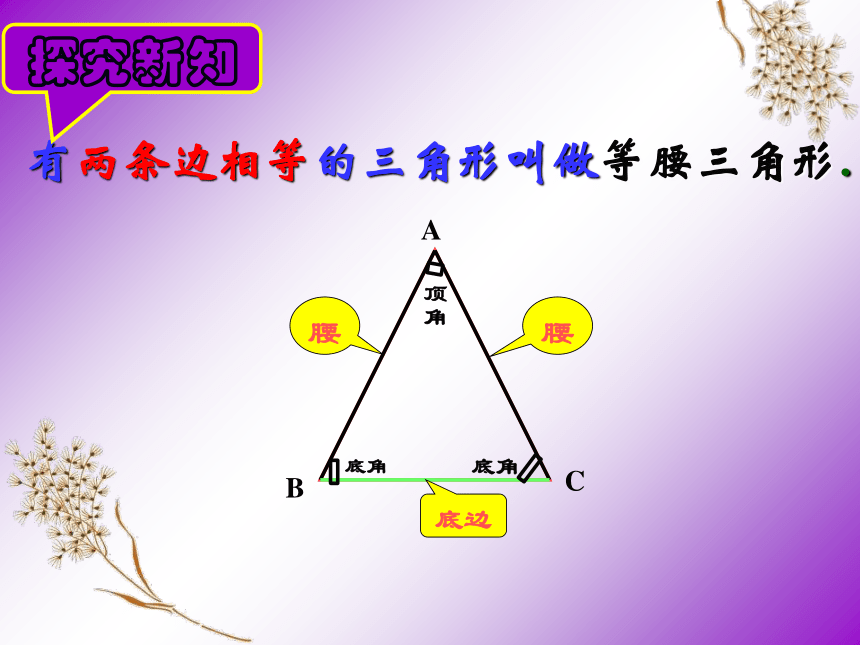
有两条边相等的三角形叫做等腰三角形.
探究新知
A
C
B
腰
腰
底边
顶角
底角
底角
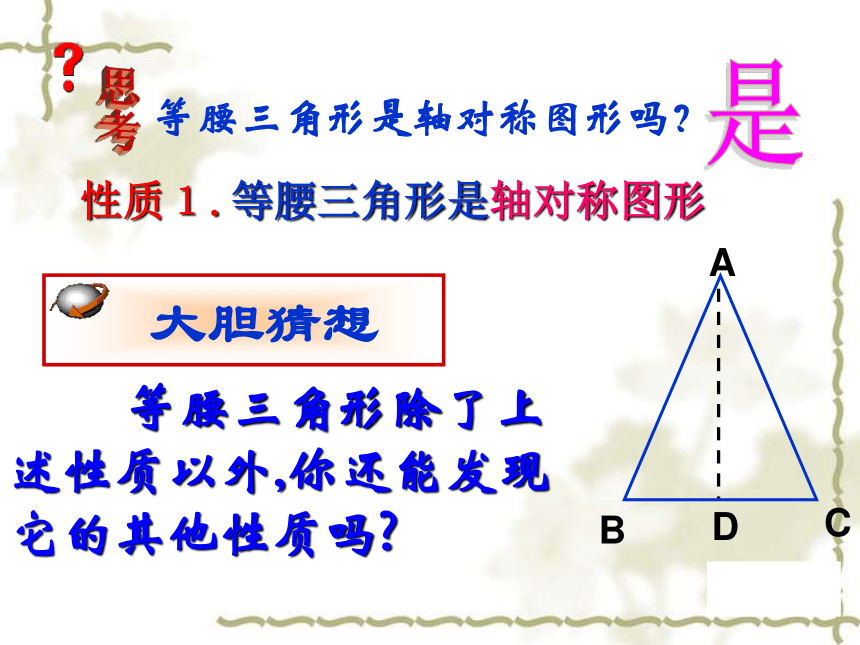
等腰三角形除了上述性质以外,你还能发现它的其他性质吗
大胆猜想
A
B
C
D
等腰三角形是轴对称图形吗?
性质1.等腰三角形是轴对称图形
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
猜想
(怎样证明两个角相等?)
A
B
C
D
A
B
C
则∠1=∠2
D
1
2
在△ABD和△ACD中
证明1: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
证明2: 作AD⊥BC于D
证明3: 作BC边的中线AD
方法2和方法3的过程
由学生独立完成
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么
A
B
C
D
性质3:等腰三角形顶角的平分线、 底边上的中线、底边上的高重合(也称为“三线合一”),它们所在的直线都是等腰三角形的对称轴。
性质2:等腰三角形的两个底角相等.(等边对等角)
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
退出
是真是假
D
(
(
1、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∴ ____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
牛刀小试:
问题解决
已知:如图房屋的顶角∠BAC=1000 ,过屋顶A的立柱AD ⊥ BC,屋椽AB=AC.
求顶架上∠B、∠C、∠BAD、∠CAD的度数.
B
A
C
D
解:在△ABC中,∵AB=AC
∴∠B=∠C
∵∠BAC=100°
∴∠B=∠C= (180°-100°)
=40°
∵AD⊥BC
∴∠BAD= ∠CAD= ∠BAC=50°
2、看谁答的又快又准
(1)等腰三角形的角平分线、中线和高互相重合.
( )
(2)有一个角是60°的等腰三角形,其它两个内
角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形.( )
x
√
√
x
如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高.
B. 某一条边上的中线.
C. 平分一角和这个角的对边的直线.
D. 某一个角的平分线.
C
等腰三角形一个角为60°,
其它两个角的度数为
.
60°、 60°
等腰三角形的周长为80厘米,若以它的底边为边的等边三角形周长为30厘米,则该等腰三角形的腰长为( )
25厘米 B. 35厘米
C. 30厘米 D. 40厘米
B
(1)等腰三角形的一个内角为100°,则
其余各角是___________.
(2)等腰三角形的一个内角为40°,则其
余各角是_____________________.
40°、 40°
70°、70°
;40°、100°
①、等腰三角形是轴对称图形.
③、等腰三角形顶角的平分线、底边上的中线、
底边上的高重合(也称为“三线合一”),
它们所在的直线都是等腰三角形的对称轴.
②、等腰三角形的两个底角相等.(等边对等角)
1、等腰三角形的定义.
2、等腰三角形的性质:
简单的轴对称图形(2)
——等腰三角形
1.什么叫轴对称图形?
2.线段是轴对称图形吗?
它的对称轴是什么?
3.角是轴对称图形吗?
它的对称轴是什么?
温故知新
简单的轴对称图形(2)
——等腰三角形
有两条边相等的三角形叫做等腰三角形.
探究新知
A
C
B
腰
腰
底边
顶角
底角
底角
等腰三角形除了上述性质以外,你还能发现它的其他性质吗
大胆猜想
A
B
C
D
等腰三角形是轴对称图形吗?
性质1.等腰三角形是轴对称图形
猜想与论证
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC
求证:∠B= C
猜想
(怎样证明两个角相等?)
A
B
C
D
A
B
C
则∠1=∠2
D
1
2
在△ABD和△ACD中
证明1: 作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
证明2: 作AD⊥BC于D
证明3: 作BC边的中线AD
方法2和方法3的过程
由学生独立完成
想一想:
刚才的证明除了能得到∠B=∠C 你还能发现什么
A
B
C
D
性质3:等腰三角形顶角的平分线、 底边上的中线、底边上的高重合(也称为“三线合一”),它们所在的直线都是等腰三角形的对称轴。
性质2:等腰三角形的两个底角相等.(等边对等角)
·→ 画出任意一个等腰三角形的底角平分线、腰上的中线和高,看看它们是否重合?
“三线合一”应该对应等腰三角形的顶角平分线,底边上的中线和底边上的高
退出
是真是假
D
(
(
1、如图,在△ABC中,AB=AC时,
(1)∵AD⊥BC
∴∠ ____= ∠_____;____=____
(2) ∵AD是中线
∴____⊥____; ∠_____= ∠_____
(3) ∵ AD是角平分线
∴ ____ ⊥____;_____=____
B
A
C
D
BAD
CAD
BD
CD
AD
BC
BAD
CAD
AD
BC
BD
CD
牛刀小试:
问题解决
已知:如图房屋的顶角∠BAC=1000 ,过屋顶A的立柱AD ⊥ BC,屋椽AB=AC.
求顶架上∠B、∠C、∠BAD、∠CAD的度数.
B
A
C
D
解:在△ABC中,∵AB=AC
∴∠B=∠C
∵∠BAC=100°
∴∠B=∠C= (180°-100°)
=40°
∵AD⊥BC
∴∠BAD= ∠CAD= ∠BAC=50°
2、看谁答的又快又准
(1)等腰三角形的角平分线、中线和高互相重合.
( )
(2)有一个角是60°的等腰三角形,其它两个内
角也为60°. ( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形.( )
x
√
√
x
如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高.
B. 某一条边上的中线.
C. 平分一角和这个角的对边的直线.
D. 某一个角的平分线.
C
等腰三角形一个角为60°,
其它两个角的度数为
.
60°、 60°
等腰三角形的周长为80厘米,若以它的底边为边的等边三角形周长为30厘米,则该等腰三角形的腰长为( )
25厘米 B. 35厘米
C. 30厘米 D. 40厘米
B
(1)等腰三角形的一个内角为100°,则
其余各角是___________.
(2)等腰三角形的一个内角为40°,则其
余各角是_____________________.
40°、 40°
70°、70°
;40°、100°
①、等腰三角形是轴对称图形.
③、等腰三角形顶角的平分线、底边上的中线、
底边上的高重合(也称为“三线合一”),
它们所在的直线都是等腰三角形的对称轴.
②、等腰三角形的两个底角相等.(等边对等角)
1、等腰三角形的定义.
2、等腰三角形的性质:
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
