19.1.2平行四边形的判定(第一课时)
文档属性
| 名称 | 19.1.2平行四边形的判定(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 665.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-01-10 16:24:10 | ||
图片预览



文档简介
课件30张PPT。19.1.2 平行四边形的判定(1)一、知识目标:
1、经历并了解平行四边形的判别方法探索过程,我们可以逐步掌握说理的基本方法。
2、探索并了解平行四边形的判别方法:两条对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形。能根据判别方法进行有关的应用。
二、能力目标:
在探索过程中发展我们的合理推理意识、主动探究的习惯。 三、德育目标:
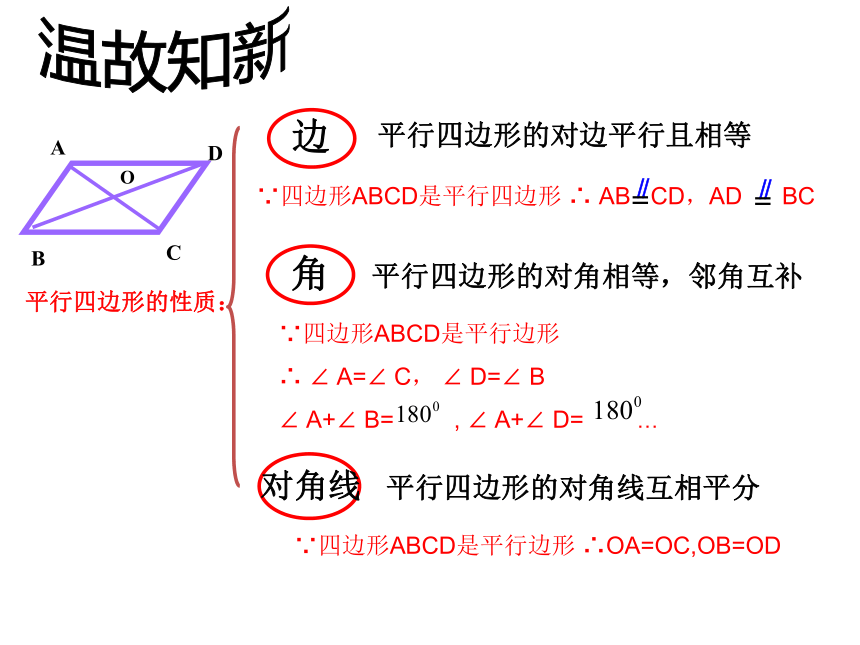
体验数学活动来源于生活又服务于生活,提高我们的学习兴趣。 教学目标:平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
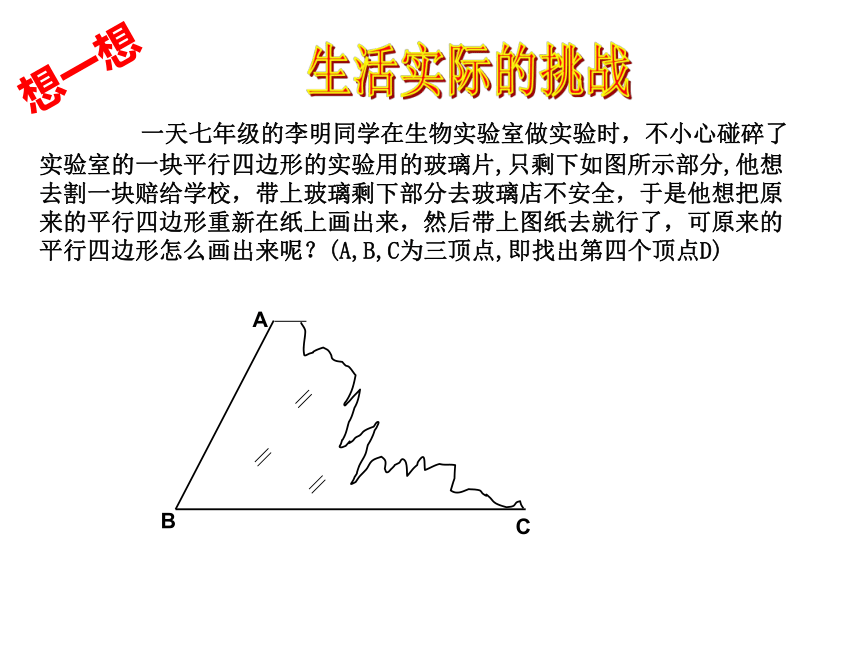
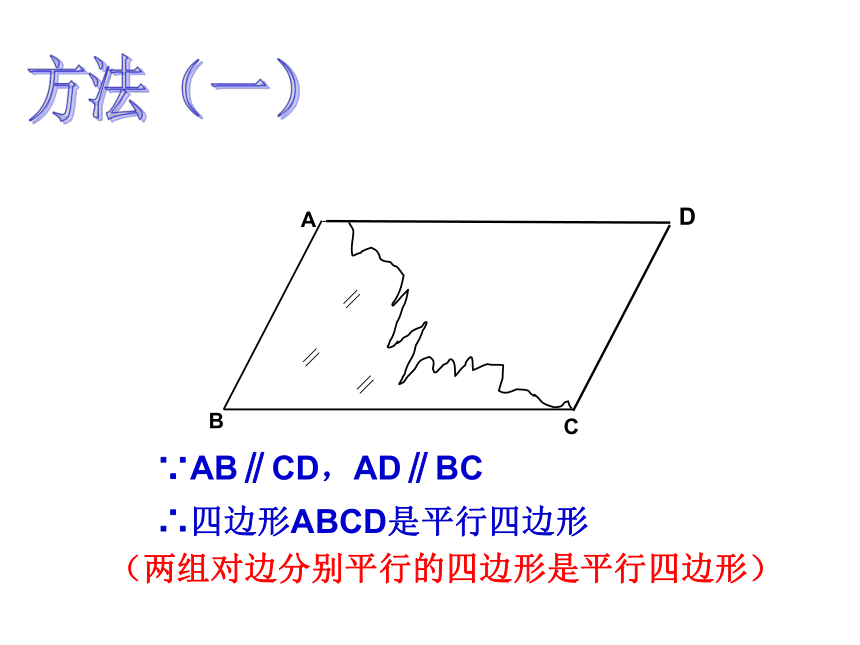
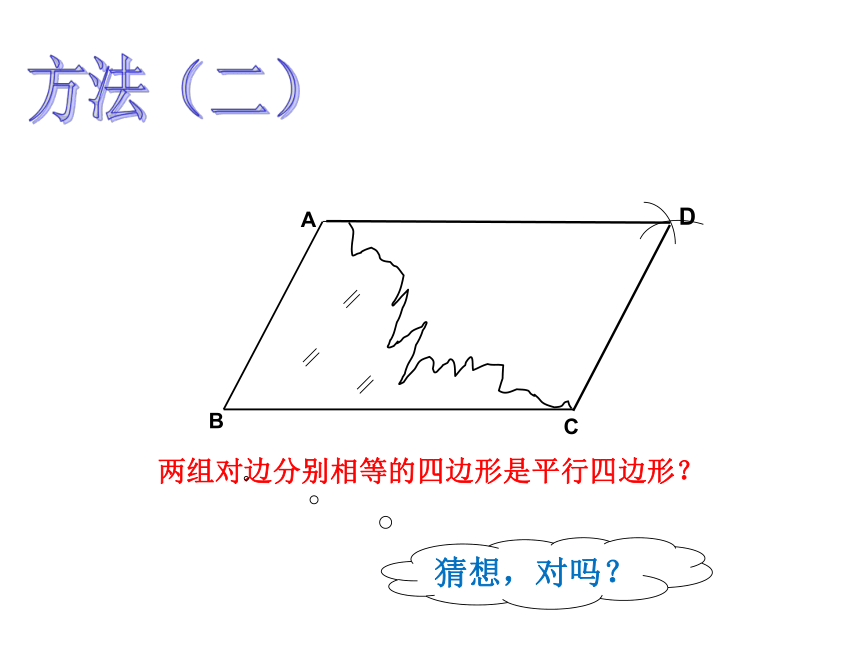
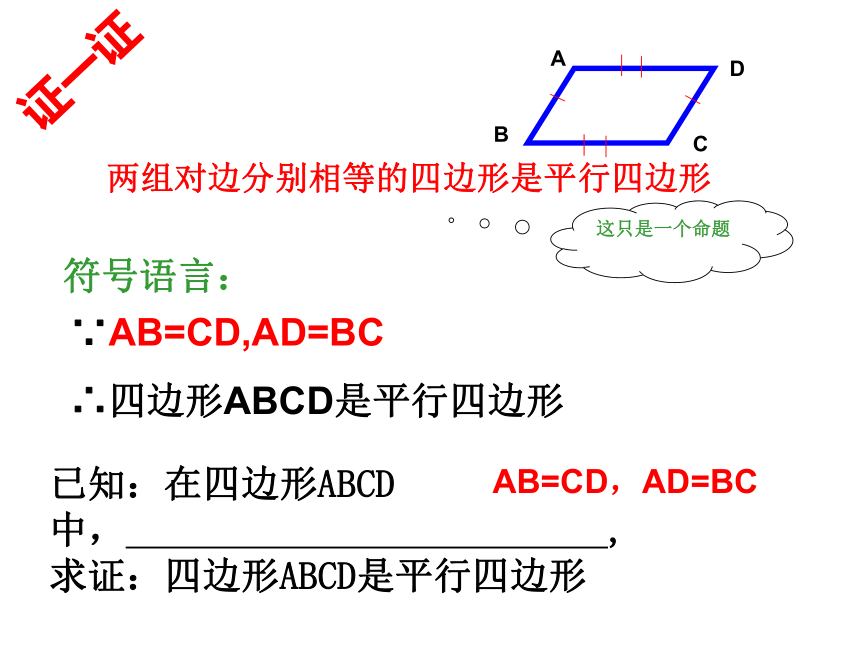
所以四边形ABCD是平行四边形。 一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形?猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC
∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC证一证已知:四边形ABCD, AB=CD,AD=BC
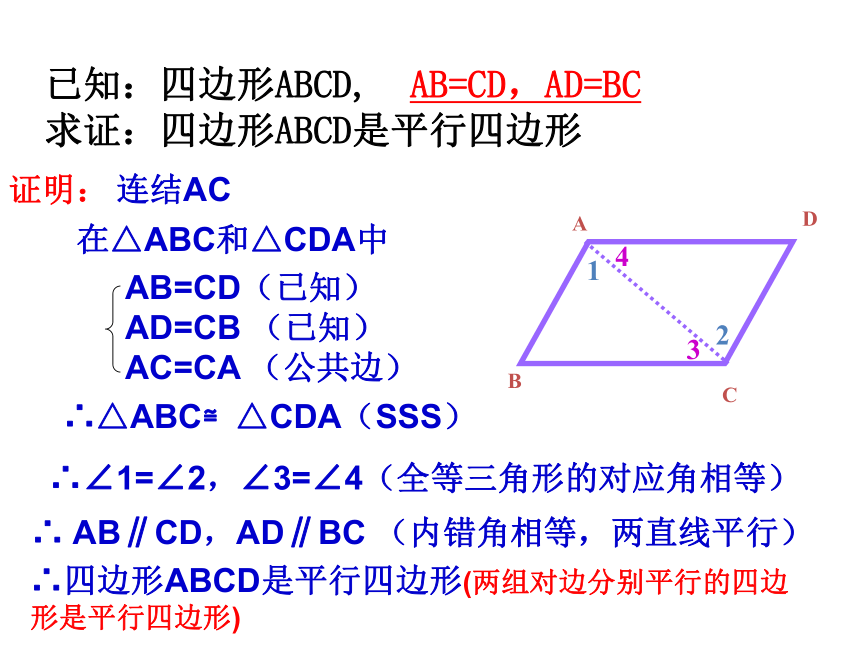
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
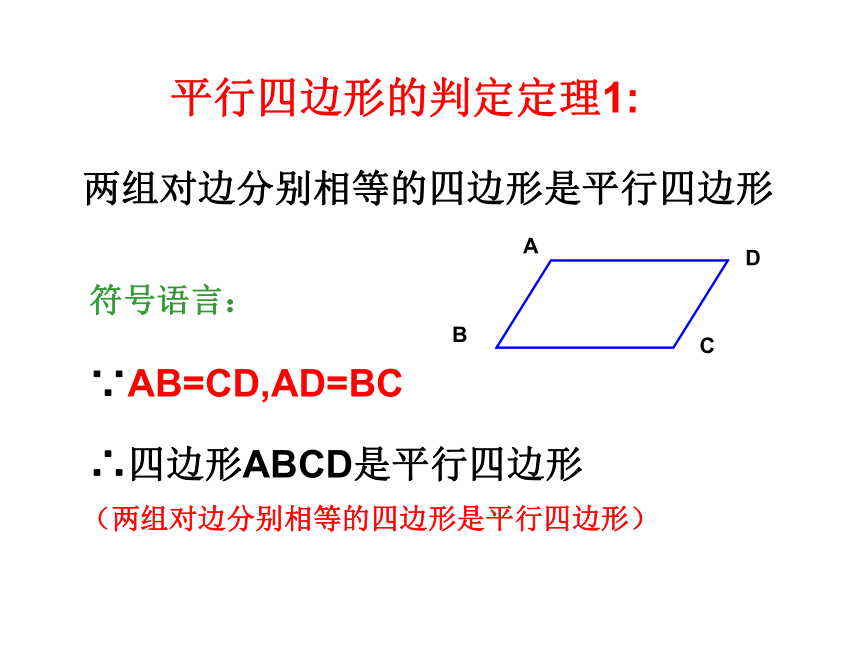
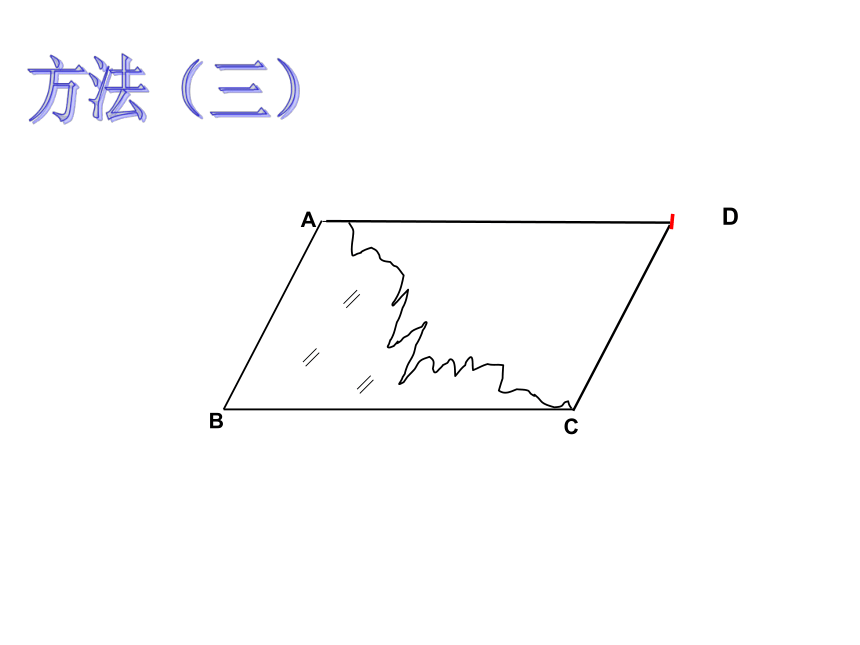
两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)方法(三)DCD一组对边平行且相等的四边形是平行四边形?猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别平行的四边形是平行四边形)
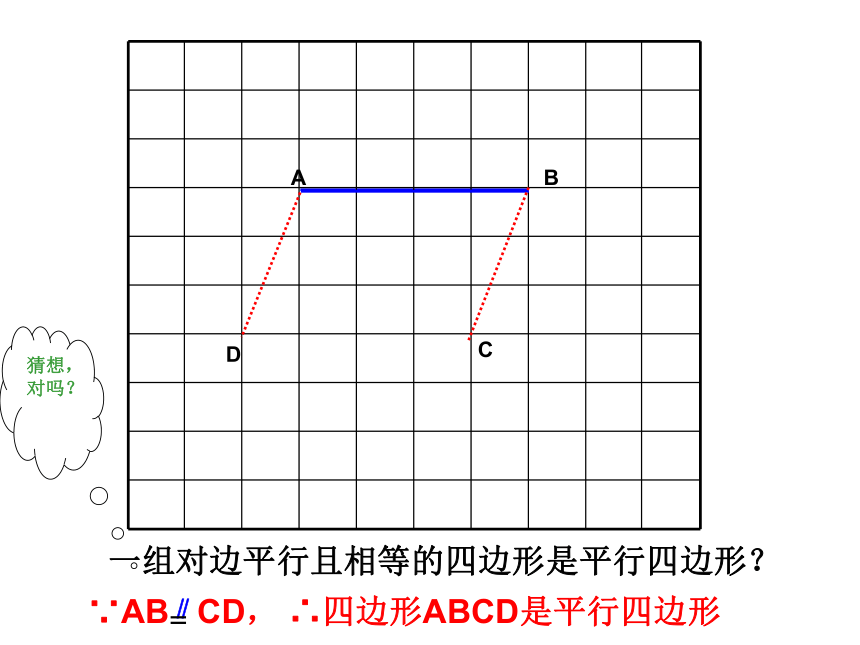
你还有其他证法吗?一组对边平行且相等的四边形是平行四边形平行四边形的判定定理2:符号语言:∵AB CD∴四边形ABCD是平行四边形 (一组对边平行且相等的四边形是平行四边形)方法(四)D两组对角分别相等的四边形是平行四边形?猜想,对吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形平行四边形的判定定理3:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)方法(五)DO对角线互相平分的四边形是平行四边形?猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△COB中∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
BAC21D(一组对边平行且相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形平行四边形的判定定理4:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法 1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形?理由是什么?试一试2.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF3、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)大显身手证法1: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
2.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决。(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”作业布置: 课本P91 4、5、10
1、经历并了解平行四边形的判别方法探索过程,我们可以逐步掌握说理的基本方法。
2、探索并了解平行四边形的判别方法:两条对角线互相平分的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形。能根据判别方法进行有关的应用。
二、能力目标:
在探索过程中发展我们的合理推理意识、主动探究的习惯。 三、德育目标:
体验数学活动来源于生活又服务于生活,提高我们的学习兴趣。 教学目标:平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD我们知道了平行四边形的性质,那么,有哪些方法可以判断一个四边形是平行四边形呢?
(1)根据定义:两组对边分别平行的四边形叫做平行四边形
因为AB//CD,AD//BC;
所以四边形ABCD是平行四边形。 一天七年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战想一想方法(一)D(两组对边分别平行的四边形是平行四边形)∵AB∥CD,AD∥BC ∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形?猜想,对吗? 两组对边分别相等的四边形是平行四边形这只是一个命题∵AB=CD,AD=BC
∴四边形ABCD是平行四边形已知:在四边形ABCD中, ,
求证:四边形ABCD是平行四边形符号语言:AB=CD,AD=BC证一证已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:连结AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠1=∠2,∠3=∠4(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
DBAC2134∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)
两组对边分别相等的四边形是平行四边形平行四边形的判定定理1:符号语言:∵AB=CD,AD=BC∴四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)方法(三)DCD一组对边平行且相等的四边形是平行四边形?猜想,对吗?求证:四边形ABCD是平行四边形。 证明:连接AC ∵AD∥BC ∴∠DAC=∠ACB又∵AD=BC,AC=AC, ∴ΔABC≌ΔCDA∴∠BAC=∠ACD∴AB∥CD ∴四边形ABCD是平行四边形 已知:在四边形ABCD中, AD BC。(两组对边分别平行的四边形是平行四边形)
你还有其他证法吗?一组对边平行且相等的四边形是平行四边形平行四边形的判定定理2:符号语言:∵AB CD∴四边形ABCD是平行四边形 (一组对边平行且相等的四边形是平行四边形)方法(四)D两组对角分别相等的四边形是平行四边形?猜想,对吗?已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形)同理可证AB∥CD
又∵∠A+ ∠B+ ∠C+ ∠D =360 °∴ 2∠A+ 2∠B=360 °∵∠A=∠C,∠B=∠D(已知)
即∠A+ ∠B=180 °∴ AD∥BC (同旁内角互补,两直线平行)
两组对角分别相等的四边形是平行四边形平行四边形的判定定理3:符号语言:∵∠A=∠C,∠B=∠D∴四边形ABCD是平行四边形(两组对角分别相等的四边形是平行四边形)方法(五)DO对角线互相平分的四边形是平行四边形?猜想,对吗?O已知:四边形ABCD, 对角线AC、BD相交于点O,且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
证明:在△AOD和△COB中∴△AOD≌△COB(SAS)
∴∠1=∠2 AD=CB(全等三角形的对应角、对应边相等)
∴ AD∥CB(内错角相等,两直线平行)
∴四边形ABCD是平行四边形
BAC21D(一组对边平行且相等的四边形是平行四边形)对角线互相平分的四边形是平行四边形平行四边形的判定定理4:符号语言:O∵ OA=OC,OB=OD∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形)从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法 1、请你向同学们展示一下你的作品-----平行四边形,同时也向同学简要介绍一下你制作的过程,为什么你能确定你制作的四边形一定是平行四边形?理由是什么?试一试2.如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF3、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝4、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)大显身手证法1: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手1.已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证法2:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
2.已知:如图,E,F分别是 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AB∥CD (平行四边形的定义)AD=BC(平行四边形的对边分别相等),∵E,F分别是AD,BC的中点,∴四边形EBFD是平行四边形(一组对边 平行并且相等的四边形是平行四边形)。∴BE=DF(平行四边形的对边分别相等)。说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决。(1)解决一个数学问题,常要通过“动手实践”----“ 猜想”----“验证猜想(证明)”-----“得出结论”作业布置: 课本P91 4、5、10
