2021-2022学年人教版八年级数学下册18.2特殊平行四边形优生辅导测评(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册18.2特殊平行四边形优生辅导测评(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 401.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 19:32:32 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学下册《18-2特殊平行四边形》优生辅导测评(附答案)
一.选择题(共8小题,满分32分)
1.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形 B.有一个角是直角的平行四边形是矩形
C.有两个角是直角的四边形是矩形 D.有一个角是直角一组对边平行的四边形是矩形
2.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A.8 B.8 C.4 D.6
4.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A.100° B.105° C.110° D.120°
5.如图,O是正方形ABCD内一点,四边形OHBE与OGDF也都是正方形,图中阴影部分的面积是10,则EG长为( )
A. B. C.10 D.20
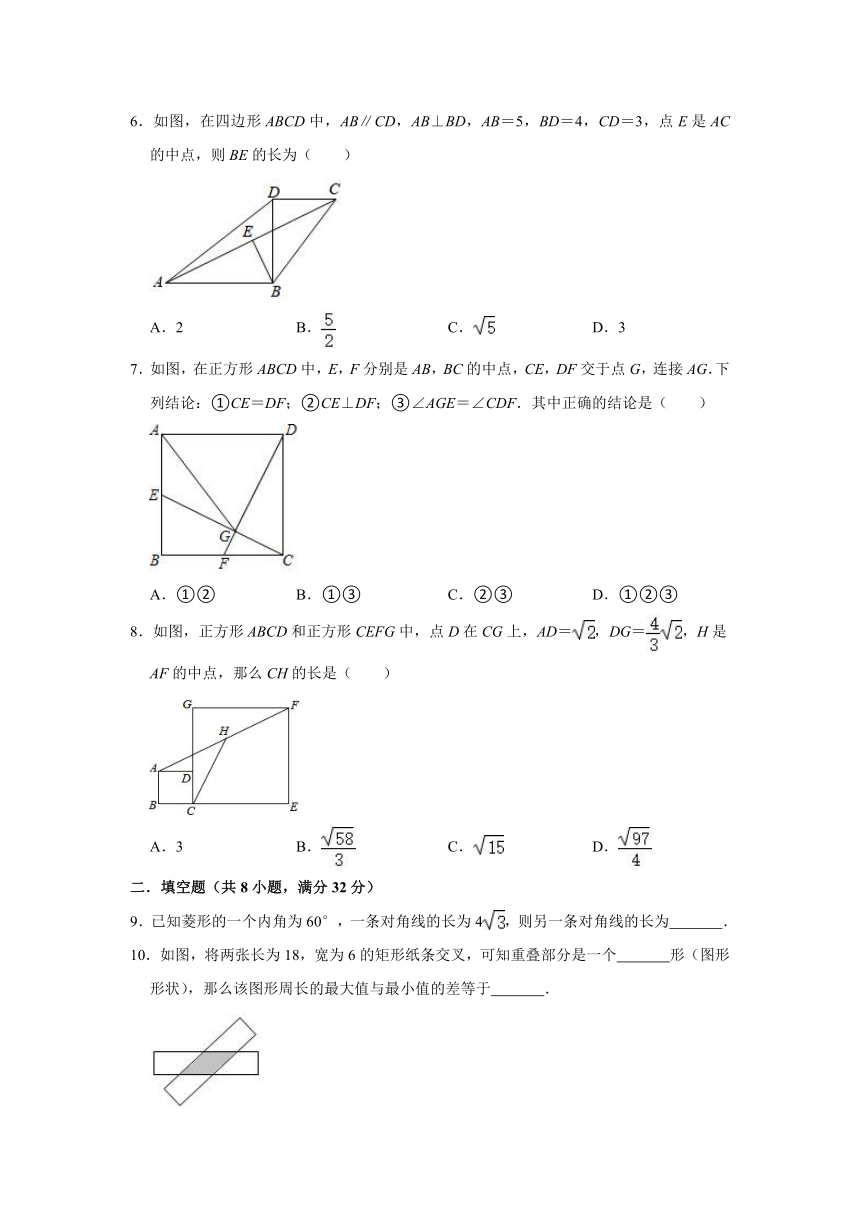
6.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
7.如图,在正方形ABCD中,E,F分别是AB,BC的中点,CE,DF交于点G,连接AG.下列结论:①CE=DF;②CE⊥DF;③∠AGE=∠CDF.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
8.如图,正方形ABCD和正方形CEFG中,点D在CG上,AD=,DG=,H是AF的中点,那么CH的长是( )
A.3 B. C. D.
二.填空题(共8小题,满分32分)
9.已知菱形的一个内角为60°,一条对角线的长为4,则另一条对角线的长为 .
10.如图,将两张长为18,宽为6的矩形纸条交叉,可知重叠部分是一个 形(图形形状),那么该图形周长的最大值与最小值的差等于 .
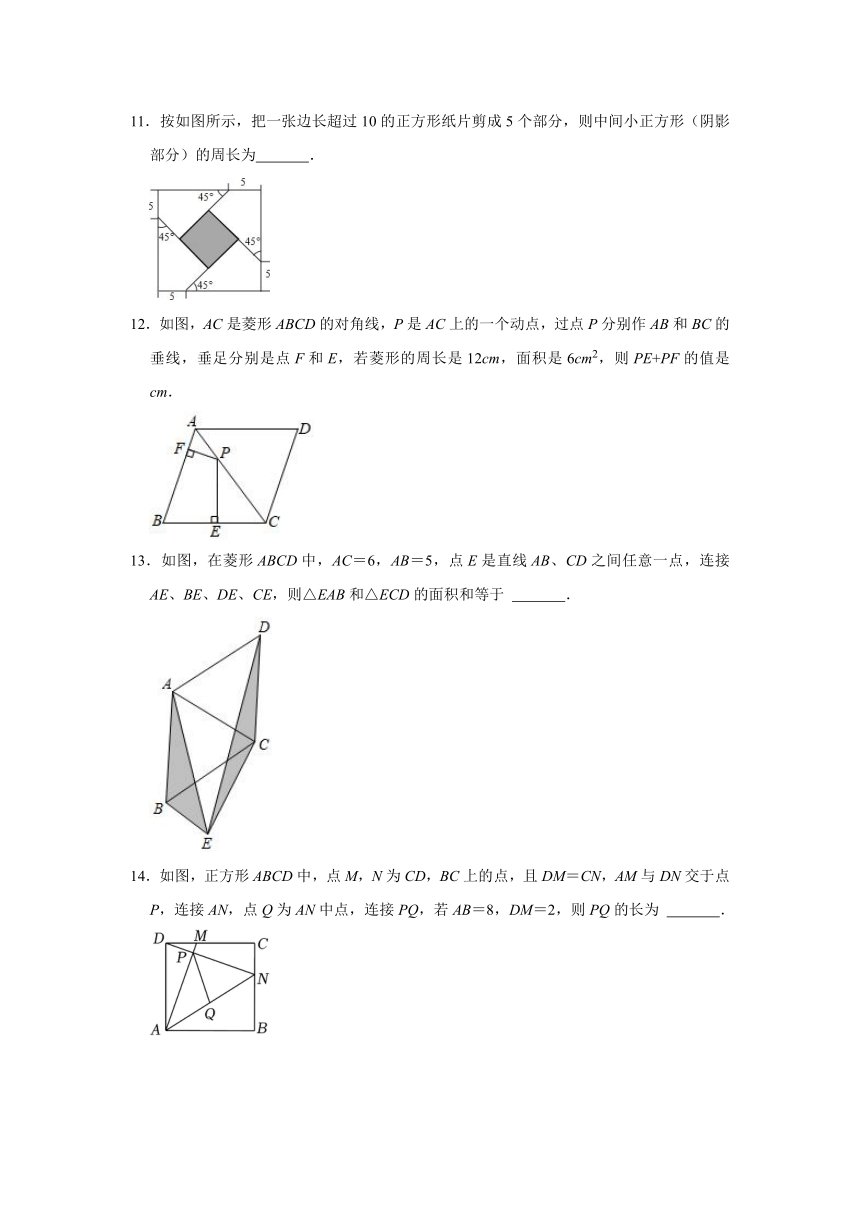
11.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为 .
12.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是 cm.
13.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
14.如图,正方形ABCD中,点M,N为CD,BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN中点,连接PQ,若AB=8,DM=2,则PQ的长为 .
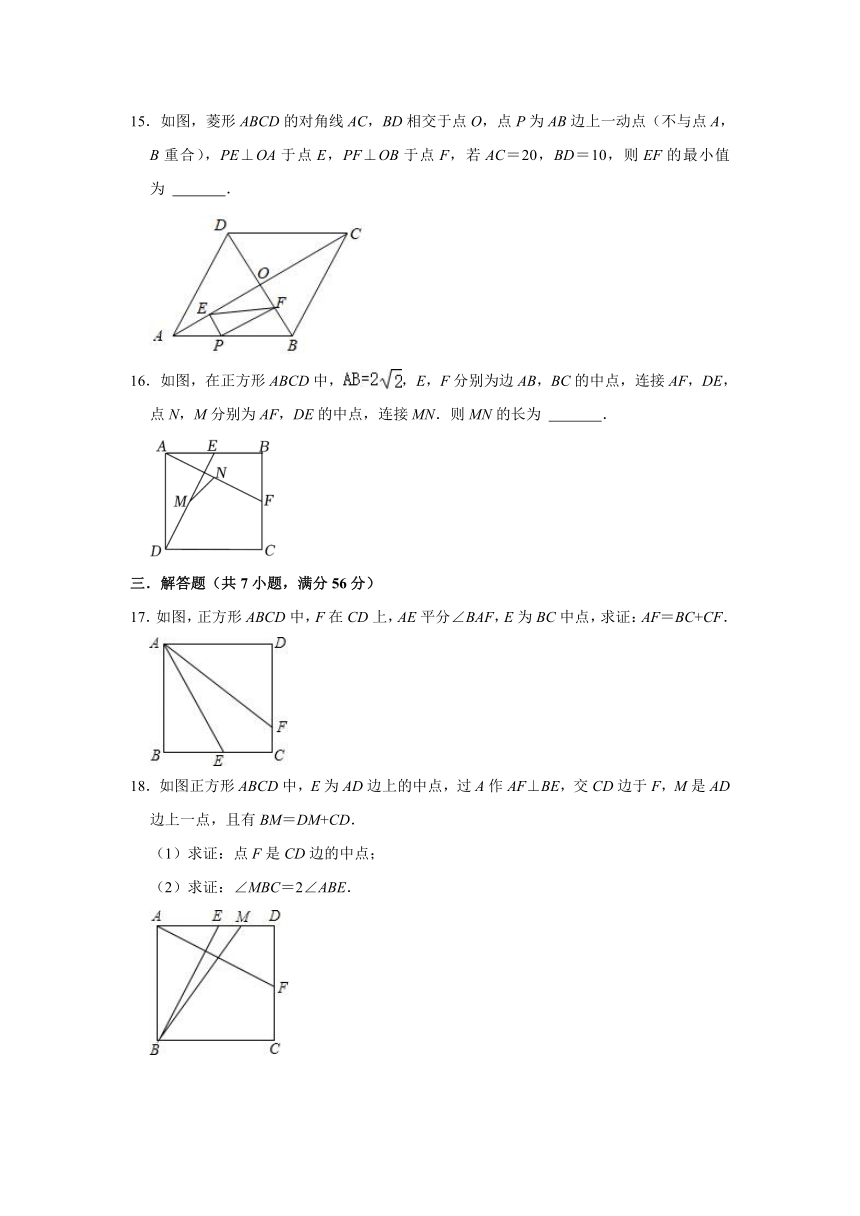
15.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AC=20,BD=10,则EF的最小值为 .
16.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN.则MN的长为 .
三.解答题(共7小题,满分56分)
17.如图,正方形ABCD中,F在CD上,AE平分∠BAF,E为BC中点,求证:AF=BC+CF.
18.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
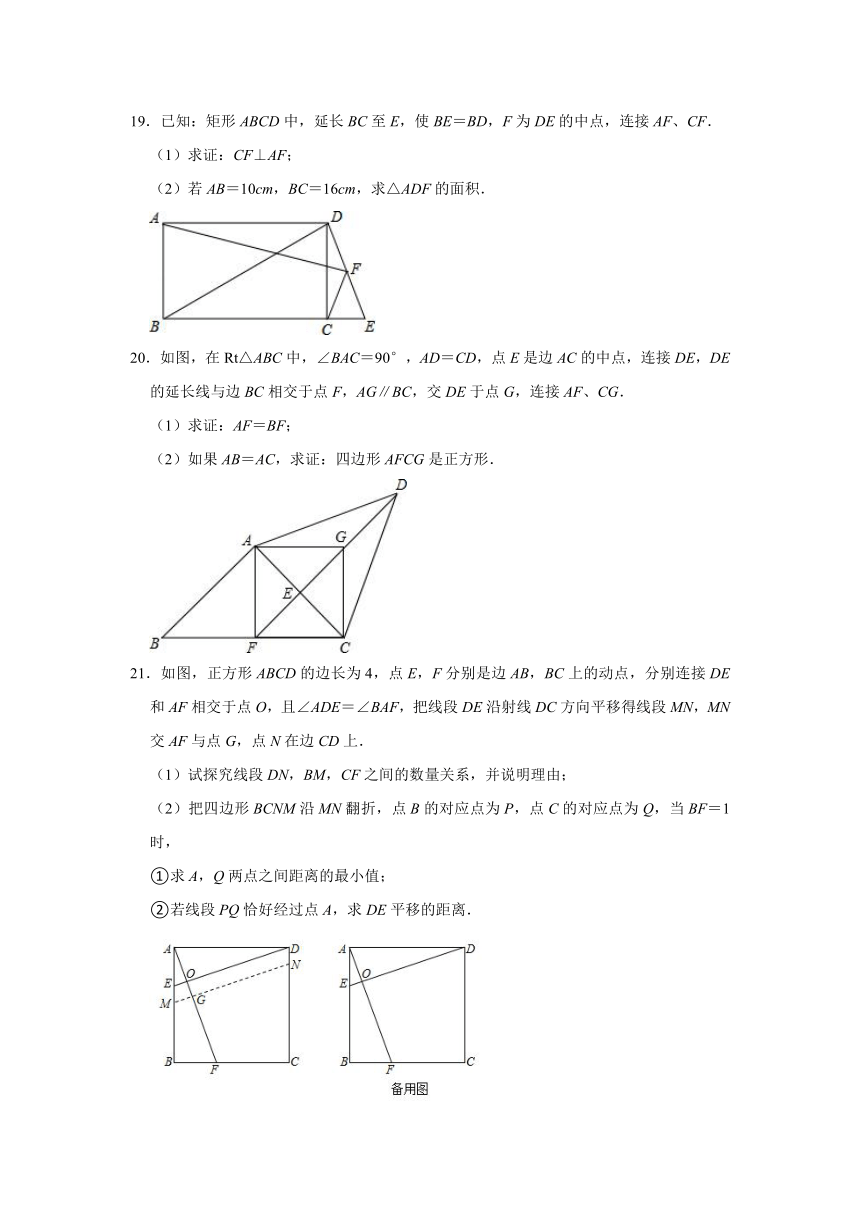
19.已知:矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连接AF、CF.
(1)求证:CF⊥AF;
(2)若AB=10cm,BC=16cm,求△ADF的面积.
20.如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.
21.如图,正方形ABCD的边长为4,点E,F分别是边AB,BC上的动点,分别连接DE和AF相交于点O,且∠ADE=∠BAF,把线段DE沿射线DC方向平移得线段MN,MN交AF与点G,点N在边CD上.
(1)试探究线段DN,BM,CF之间的数量关系,并说明理由;
(2)把四边形BCNM沿MN翻折,点B的对应点为P,点C的对应点为Q,当BF=1时,
①求A,Q两点之间距离的最小值;
②若线段PQ恰好经过点A,求DE平移的距离.
22.已知正方形ABCD的边长为4,点E在BC上,CE=1,线段MN在对角线AC上.MN=,连BM,EN.
(1)如图1,当点N是AC的中点时,求BM+EN的值;
(2)如图2,当点M是AC的中点时,求BM+EN的值;
(3)当线段MN在对角线AC上运动时,BM+EN的最小值为 .
23.综合与实践
(1)如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,则MN,AM,CN的数量关系为 .
(2)如图2,在四边形ABCD中,BC∥AD,AB=BC,∠A+∠C=180°,点M、N分别在AD、CD上,若∠MBN=∠ABC,试探索线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
(3)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=∠ABC,试探究线段MN、AM、CN的数量关系为 .
参考答案
一.选择题(共8小题,满分32分)
1.解:A中对角线互相垂直的平行四边形是菱形,A错;
B中有一个角是直角的平行四边形是矩形,矩形的判定,正确;
C中也可能是直角梯形,C错;
D中也可能是直角梯形,D错;
故选:B.
2.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=30°,
∵OA=OD,
∴∠ODA=∠DAC=30°,
∴∠DOC=60°,
∵OD=OC,
∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°
∴∠DAC=∠ACB=30°,
∴AC=2AB,
∵AC>BC,
∴2AB>BC,∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°,
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE,
∵四边形ABCD是矩形,
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD,
∴BE=BO,
∴∠BOE=∠BEO=(180°﹣∠OBE)=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等得出S△AOE=S△COE,∴④正确;
故选:C.
3.解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在RT△BFO和RT△BFC中,
,
∴RT△BFO≌RT△BFC,
∴BO=BC,
在RT△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故选:D.
4.解:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠A=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AEF是等边三角形,AE=AB,
∴∠AEF=∠AFE=60°,AF=AD,
∴∠B=∠AEB,∠D=∠AFD,
由三角形的内角和定理得:∠BAE=∠FAD,
设∠BAE=∠FAD=x,
则∠D=∠AFD=180°﹣60°﹣2x,
∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°﹣60°﹣2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°,
故选:A.
5.解:如图,连接AO,
∵四边形OHBE,四边形OGDF都是正方形,
∴FO=OG,HO=OE,
∵阴影部分的面积是10,
∴×OG×OF+×OE×OH=10,
∴OG2+OE2=20,
∴EG2=20,
∴EG=2,
故选:B.
6.解:过点C作CF⊥AB的延长线于点F,如图所示:
∵AB∥CD,AB⊥BD,
∴CD⊥BD,
∵CF⊥AB,
∴CF⊥CD,
∴BD∥CF,
∴四边形BFCD是矩形,
∴BF=CD=3,CF=BD=4,
在Rt△BCF中,BC=,
在Rt△AFC中,AC==,
∴BC=AB=5,
∴△ABC是等腰三角形,
∵点E是AC的中点,
∴BE⊥AC,
∵,
∴×5×4=×BE,
解得:BE=.
故选:C.
7.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵E,F分别是AB,BC的中点,
∴BE=AB,CF=BC,
∴BE=CF,
在△CBE与△DCF中,
,
∴△CBE≌△DCF(SAS),
∴∠ECB=∠CDF,CE=DF,故①正确;
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故②正确;
∴∠EGD=90°,
延长CE交DA的延长线于H,
∵点E是AB的中点,
∴AE=BE,
∵∠AHE=∠BCE,∠AEH=∠CEB,AE=BE,
∴△AEH≌△BEC(AAS),
∴BC=AH=AD,
∵AG是斜边的中线,
∴AG=DH=AD,
∴∠ADG=∠AGD,
∵∠AGE+∠AGD=90°,∠CDF+∠ADG=90°,
∴∠AGE=∠CDF.故③正确;
故选:D.
8.解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,AD=,DG=,
∴AC=2,CG=,
∴CF=,
∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF=,
∵H是AF的中点,
∴CH=AF=×=.
故选:B.
二.填空题(共8小题,满分32分)
9.解:①当较长对角线长为4时,则另一对角线长为=4;
②当较短对角线长为4时,则另一对角线长为=12;
故另一条对角线的长为12或4.
故答案为:12或4.
10.解:重叠部分是一个菱形,
当两张纸条如图1所示放置时,菱形周长最大,
设这时菱形的边长为xcm,
由勾股定理:x2=(18﹣x)2+62,
解得:x=10,
∴4x=40,
即菱形的最大周长为40cm.
当两张纸条如图所2示放置时,即是正方形时取得最小值为:4×6=24.
∴菱形周长的最大值与最小值的和是40﹣24=16,
故答案为:16.
11.解:延长BG,交AE与点C,
∵∠ABC=45°
∴△ABC是等腰直角三角形,
∴AB=AC
∴CE=5
∵△CED是等腰直角三角形,
∴CD=5
∵CD=GF,
∴中间的小正方形的边长是5,因而周长是20.
故答案为20
12.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
13.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积=×==12.
故答案为:12
14.解:在正方形ABCD中,
AD=CD,∠ADC=∠DCN=90°,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS),
∴∠DAM=∠CDN,∠DMA=∠CND,
∵∠DAM+∠AMD=90°,
∴∠PDM+∠DMP=90°,
∴∠DPM=90°,
∵∠DPM=∠APN,
∴△ANP为直角三角形,
∴AN为直角三角形的斜边,由直角三角形的性质得PQ=AN,
∵DM=CN=2,BC=CD=AB=8,
∴BN=BC﹣CN=6,
在△ANB中,AN===10,
∴PQ=5.
故答案为:5..
15.解:连接OP,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=10,BD=BD=5,
∴AB==5,
∵PE⊥OA于点E,PF⊥OB于点F,
∴∠EOF=∠OEP=∠OFP=90°,
∴四边形OEPF是矩形,
∴EF=OP,
∵当OP取最小值时,EF的值最小,
∴当OP⊥AB时,OP最小,
∴S△ABO=OA OB=AB OP,
∴OP==2,
∴EF的最小值为2,
故答案为:2.
16.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故答案为:1.
三.解答题(共7小题,满分56分)
17.证明:作EM⊥AF于M,连接EF,
∵∠B=90°,
∴∠B=∠AME=90°,
∵∠1=∠2,
∴BE=EM,
在Rt△ABE与Rt△AME中,
,
∴Rt△ABE≌Rt△AME(HL),
∴AM=AB=BC,EM=BE,
∵E是BC中点,
∴EC=BE=EM,
在Rt△EMF与Rt△ECF中,
,
∴Rt△EMF≌Rt△ECF(HL),
∴FM=FC,
∵AF=AM+MF,
∴AF=BC+CF.
18.(1)证明:∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)证明:延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,
∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
19.(1)证明:如图,连接BF,在矩形ABCD中,AD=BC,∠ADC=∠BCD=90°,
∵F为DE的中点,
∴CF=DF,
∴∠CDF=∠DCF,
∴∠ADC+∠CDF=∠BCD+∠DCF,
即∠ADF=∠BCF,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(SAS),
∴∠AFD=∠BFC,
∵BE=BD,F为DE的中点,
∴BF⊥DE,
∴∠AFC=∠AFB+∠BFC=∠AFB+∠AFD=90°,
∴CF⊥AF;
(2)解:∵△ADF≌△BCF,
∴点F到AD、BC的距离相等,
∵AB=10cm,
∴点F到AD的距离为×10=5cm,
∴△ADF的面积=×16×5=40cm2.
20.证明:(1)∵AD=CD,点E是边AC的中点,
∴DE⊥AC.
即得DE是线段AC的垂直平分线.
∴AF=CF.
∴∠FAC=∠ACB.
在Rt△ABC中,由∠BAC=90°,
得∠B+∠ACB=90°,∠FAC+∠BAF=90°.
∴∠B=∠BAF.
∴AF=BF.
(2)∵AG∥CF,∴∠AGE=∠CFE.
又∵点E是边AC的中点,∴AE=CE.
在△AEG和△CEF中,
,
∴△AEG≌△CEF(AAS).
∴AG=CF.
又∵AG∥CF,∴四边形AFCG是平行四边形.
∵AF=CF,∴四边形AFCG是菱形.
在Rt△ABC中,由AF=CF,AF=BF,得BF=CF.
即得点F是边BC的中点.
又∵AB=AC,∴AF⊥BC.即得∠AFC=90°.
∴四边形AFCG是正方形.
21.解:(1)结论:DN+BM=CF.
理由:如图1中,
∵四边形ABCD是正方形,
∴AD=AB=BC,AB∥CD,∠B=∠DAE=90°,
∵∠ADE=∠BAF,
∴△DAE≌△BAF(ASA),
∴AE=BF,
∵BA=BC,
∴BE=CF,
∵EM∥DN,DE∥MN,
∴四边形MNDE是平行四边形,
∴DN=EN,
∴DN+BM=EN+BM=BE=CF.
(2)①如图2中,连接CQ交AD于T.
由翻折的性质可知,CQ⊥MN,
∵∠BAF+∠DAF=90°,∠ADE=∠BAF,
∴∠ADE+∠DAF=90°,
∴∠AOD=90°,
∴AF⊥DE,
∵MN∥DE,
∴MN⊥AF,
∴CQ∥AF,
∵AT∥CF,
∴四边形AFCT是平行四边形,
∴AT=CF=4﹣1=3,
∴DT=AD﹣AT=1,
∴点Q的运动轨迹是射线CQ,当AQ⊥CQ时,AQ的值最小,
在Rt△ABF中,AF===,
∵AF∥CQAQ⊥CQ,
∴AQ⊥AF,
∴∠QAF=∠BAD=90°,
∴∠QAT=∠BAF,
∵∠AQT=∠B=90°,
∴AQ=,
∴AQ的最小值为.
②如图3中,连接MF.
∵线段PQ恰好经过点A,由翻折的性质可知,GA=FG,
∵MN⊥AF,
∴MA=MF,
设MA=MF=x,
在Rt△BFM中 BM2+BF2=MF2,
∴(4﹣x)2+12=x2,
∴x=,
∵AE=BF=1,
∴EM=AM﹣AE=﹣1=,
∴DE的平移距离为.
22.解:(1)连接BN,过N作NH⊥BC于H,如图1所示,
∵正方形ABCD,N为AC中点,
∴△ANB与△BHN都为等腰直角三角形,
∴AN=BN=AB=2,NH=CH=BN=2,
在Rt△BNM中,由勾股定理得:BM===,
在Rt△NHE中,NH=2,HE=2﹣1=1,EN==,
则BM+EN=+;
(2)∵正方形ABCD,M为AC中点,
∴BM=AM=CM=2,
∵MN=,
∴CN=CM﹣MN=,
若过N作NE′⊥BC于点E′,如图2所示,则得到NE′=CE′=1,
∴E′与E重合,且NE=NE′=1,
∴BM+EN=2+1;
(3)ME+EN的最小值为,理由为:
如图3所示,作出点E关于AC的对称点E′,则CE′=CE=1,
将MN平移至E′F处,则四边形MNE′F为平行四边形,
连接BF,EF,过F作FG⊥CD于G,可得△E′FG为等腰直角三角形,
∴E′F=MN=,FG=E′G=1=CE,
∴四边形CEFG为矩形,
∴EF=CG=2,BE=BC﹣CE=3,
∴BF==,
显然,BM+EN=BM+E′N=BM+FM≥BF=.
23.解:(1)结论:MN=AM+CN.
理由:如图1中,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∵四边形ABCD是正方形,
∴∠A=∠BCD=∠ABC=∠BCM′=90°,
∴∠NCM′=180°,
∴N,C,M′共线,
∵∠ABM=∠CBM′,
∴∠MBM′=∠ABC=90°,
∵∠MBN=45°,
∴∠MBN=∠M′BN=45°,
在△BNM和△BNM′中,
,
∴△NBM≌△NBM′(SAS),
∴MN=NM′,
∵AM=CM′,
∴MN=AM+CN.
故答案为:MN=AM+CN;
(2)结论:MN=AM+CN.
理由:如图2中,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC﹣∠MBN=∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(3)结论:MN=CN﹣AM.
理由:如图3中,作∠CBM′=∠ABM交CN于点M′,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠C=360°﹣180°=180°,
又∵∠BAD+∠BAM=180°,
∴∠C=∠BAM,
在△ABM和△CBM′中,
,
∴△ABM≌△CBM′(ASA),
∴AM=CM′,BM=BM′,
∵∠MBN=∠ABC,
∴∠M′BN=∠ABC﹣(∠ABN+∠CBM′)=∠ABC﹣(∠ABN+∠ABM)=∠ABC﹣∠MBN=∠ABC,
∴∠MBN=∠M′BN,
在△MBN和△M′BN中,
,
∴△MBN≌△M′BN(SAS),
∴MN=M′N,
∵M′N=CN﹣CM′=CN﹣AM,
∴MN=CN﹣AM.
故答案为:MN=CN﹣AM.
一.选择题(共8小题,满分32分)
1.下列说法正确的是( )
A.对角线互相垂直的四边形是菱形 B.有一个角是直角的平行四边形是矩形
C.有两个角是直角的四边形是矩形 D.有一个角是直角一组对边平行的四边形是矩形
2.如图所示,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下面的结论:
①△ODC是等边三角形;②BC=2AB;③∠AOE=135°;④S△AOE=S△COE,
其中正确结论有( )
A.1个 B.2个 C.3个 D.4个
3.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )
A.8 B.8 C.4 D.6
4.如图,已知四边形ABCD的四边都相等,等边△AEF的顶点E、F分别在BC、CD上,且AE=AB,则∠C=( )
A.100° B.105° C.110° D.120°
5.如图,O是正方形ABCD内一点,四边形OHBE与OGDF也都是正方形,图中阴影部分的面积是10,则EG长为( )
A. B. C.10 D.20
6.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,点E是AC的中点,则BE的长为( )
A.2 B. C. D.3
7.如图,在正方形ABCD中,E,F分别是AB,BC的中点,CE,DF交于点G,连接AG.下列结论:①CE=DF;②CE⊥DF;③∠AGE=∠CDF.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
8.如图,正方形ABCD和正方形CEFG中,点D在CG上,AD=,DG=,H是AF的中点,那么CH的长是( )
A.3 B. C. D.
二.填空题(共8小题,满分32分)
9.已知菱形的一个内角为60°,一条对角线的长为4,则另一条对角线的长为 .
10.如图,将两张长为18,宽为6的矩形纸条交叉,可知重叠部分是一个 形(图形形状),那么该图形周长的最大值与最小值的差等于 .
11.按如图所示,把一张边长超过10的正方形纸片剪成5个部分,则中间小正方形(阴影部分)的周长为 .
12.如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2,则PE+PF的值是 cm.
13.如图,在菱形ABCD中,AC=6,AB=5,点E是直线AB、CD之间任意一点,连接AE、BE、DE、CE,则△EAB和△ECD的面积和等于 .
14.如图,正方形ABCD中,点M,N为CD,BC上的点,且DM=CN,AM与DN交于点P,连接AN,点Q为AN中点,连接PQ,若AB=8,DM=2,则PQ的长为 .
15.如图,菱形ABCD的对角线AC,BD相交于点O,点P为AB边上一动点(不与点A,B重合),PE⊥OA于点E,PF⊥OB于点F,若AC=20,BD=10,则EF的最小值为 .
16.如图,在正方形ABCD中,,E,F分别为边AB,BC的中点,连接AF,DE,点N,M分别为AF,DE的中点,连接MN.则MN的长为 .
三.解答题(共7小题,满分56分)
17.如图,正方形ABCD中,F在CD上,AE平分∠BAF,E为BC中点,求证:AF=BC+CF.
18.如图正方形ABCD中,E为AD边上的中点,过A作AF⊥BE,交CD边于F,M是AD边上一点,且有BM=DM+CD.
(1)求证:点F是CD边的中点;
(2)求证:∠MBC=2∠ABE.
19.已知:矩形ABCD中,延长BC至E,使BE=BD,F为DE的中点,连接AF、CF.
(1)求证:CF⊥AF;
(2)若AB=10cm,BC=16cm,求△ADF的面积.
20.如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
(1)求证:AF=BF;
(2)如果AB=AC,求证:四边形AFCG是正方形.
21.如图,正方形ABCD的边长为4,点E,F分别是边AB,BC上的动点,分别连接DE和AF相交于点O,且∠ADE=∠BAF,把线段DE沿射线DC方向平移得线段MN,MN交AF与点G,点N在边CD上.
(1)试探究线段DN,BM,CF之间的数量关系,并说明理由;
(2)把四边形BCNM沿MN翻折,点B的对应点为P,点C的对应点为Q,当BF=1时,
①求A,Q两点之间距离的最小值;
②若线段PQ恰好经过点A,求DE平移的距离.
22.已知正方形ABCD的边长为4,点E在BC上,CE=1,线段MN在对角线AC上.MN=,连BM,EN.
(1)如图1,当点N是AC的中点时,求BM+EN的值;
(2)如图2,当点M是AC的中点时,求BM+EN的值;
(3)当线段MN在对角线AC上运动时,BM+EN的最小值为 .
23.综合与实践
(1)如图1,在正方形ABCD中,点M、N分别在AD、CD上,若∠MBN=45°,则MN,AM,CN的数量关系为 .
(2)如图2,在四边形ABCD中,BC∥AD,AB=BC,∠A+∠C=180°,点M、N分别在AD、CD上,若∠MBN=∠ABC,试探索线段MN、AM、CN有怎样的数量关系?请写出猜想,并给予证明.
(3)如图3,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M、N分别在DA、CD的延长线上,若∠MBN=∠ABC,试探究线段MN、AM、CN的数量关系为 .
参考答案
一.选择题(共8小题,满分32分)
1.解:A中对角线互相垂直的平行四边形是菱形,A错;
B中有一个角是直角的平行四边形是矩形,矩形的判定,正确;
C中也可能是直角梯形,C错;
D中也可能是直角梯形,D错;
故选:B.
2.解:∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OD=OB,AC=BD,
∴OA=OD=OC=OB,
∵AE平分∠BAD,
∴∠DAE=45°,
∵∠CAE=15°,
∴∠DAC=30°,
∵OA=OD,
∴∠ODA=∠DAC=30°,
∴∠DOC=60°,
∵OD=OC,
∴△ODC是等边三角形,∴①正确;
∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=90°
∴∠DAC=∠ACB=30°,
∴AC=2AB,
∵AC>BC,
∴2AB>BC,∴②错误;
∵AD∥BC,
∴∠DBC=∠ADB=30°,
∵AE平分∠DAB,∠DAB=90°,
∴∠DAE=∠BAE=45°,
∵AD∥BC,
∴∠DAE=∠AEB,
∴∠AEB=∠BAE,
∴AB=BE,
∵四边形ABCD是矩形,
∴∠DOC=60°,DC=AB,
∵△DOC是等边三角形,
∴DC=OD,
∴BE=BO,
∴∠BOE=∠BEO=(180°﹣∠OBE)=75°,
∵∠AOB=∠DOC=60°,
∴∠AOE=60°+75°=135°,∴③正确;
∵OA=OC,
∴根据等底等高的三角形面积相等得出S△AOE=S△COE,∴④正确;
故选:C.
3.解:如图,连接BO,
∵四边形ABCD是矩形,
∴DC∥AB,∠DCB=90°
∴∠FCO=∠EAO,
在△AOE和△COF中,
,
∴△AOE≌△COF,
∴OE=OF,OA=OC,
∵BF=BE,
∴BO⊥EF,∠BOF=90°,
∵∠FEB=2∠CAB=∠CAB+∠AOE,
∴∠EAO=∠EOA,
∴EA=EO=OF=FC=2,
在RT△BFO和RT△BFC中,
,
∴RT△BFO≌RT△BFC,
∴BO=BC,
在RT△ABC中,∵AO=OC,
∴BO=AO=OC=BC,
∴△BOC是等边三角形,
∴∠BCO=60°,∠BAC=30°,
∴∠FEB=2∠CAB=60°,∵BE=BF,
∴△BEF是等边三角形,
∴EB=EF=4,
∴AB=AE+EB=2+4=6.
故选:D.
4.解:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠A=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AEF是等边三角形,AE=AB,
∴∠AEF=∠AFE=60°,AF=AD,
∴∠B=∠AEB,∠D=∠AFD,
由三角形的内角和定理得:∠BAE=∠FAD,
设∠BAE=∠FAD=x,
则∠D=∠AFD=180°﹣60°﹣2x,
∵∠FAD+∠D+∠AFD=180°,
∴x+2(180°﹣60°﹣2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°,
故选:A.
5.解:如图,连接AO,
∵四边形OHBE,四边形OGDF都是正方形,
∴FO=OG,HO=OE,
∵阴影部分的面积是10,
∴×OG×OF+×OE×OH=10,
∴OG2+OE2=20,
∴EG2=20,
∴EG=2,
故选:B.
6.解:过点C作CF⊥AB的延长线于点F,如图所示:
∵AB∥CD,AB⊥BD,
∴CD⊥BD,
∵CF⊥AB,
∴CF⊥CD,
∴BD∥CF,
∴四边形BFCD是矩形,
∴BF=CD=3,CF=BD=4,
在Rt△BCF中,BC=,
在Rt△AFC中,AC==,
∴BC=AB=5,
∴△ABC是等腰三角形,
∵点E是AC的中点,
∴BE⊥AC,
∵,
∴×5×4=×BE,
解得:BE=.
故选:C.
7.解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=90°,
∵E,F分别是AB,BC的中点,
∴BE=AB,CF=BC,
∴BE=CF,
在△CBE与△DCF中,
,
∴△CBE≌△DCF(SAS),
∴∠ECB=∠CDF,CE=DF,故①正确;
∵∠BCE+∠ECD=90°,
∴∠ECD+∠CDF=90°,
∴∠CGD=90°,
∴CE⊥DF,故②正确;
∴∠EGD=90°,
延长CE交DA的延长线于H,
∵点E是AB的中点,
∴AE=BE,
∵∠AHE=∠BCE,∠AEH=∠CEB,AE=BE,
∴△AEH≌△BEC(AAS),
∴BC=AH=AD,
∵AG是斜边的中线,
∴AG=DH=AD,
∴∠ADG=∠AGD,
∵∠AGE+∠AGD=90°,∠CDF+∠ADG=90°,
∴∠AGE=∠CDF.故③正确;
故选:D.
8.解:如图,连接AC、CF,
∵正方形ABCD和正方形CEFG中,AD=,DG=,
∴AC=2,CG=,
∴CF=,
∠ACD=∠GCF=45°,
∴∠ACF=90°,
由勾股定理得,AF=,
∵H是AF的中点,
∴CH=AF=×=.
故选:B.
二.填空题(共8小题,满分32分)
9.解:①当较长对角线长为4时,则另一对角线长为=4;
②当较短对角线长为4时,则另一对角线长为=12;
故另一条对角线的长为12或4.
故答案为:12或4.
10.解:重叠部分是一个菱形,
当两张纸条如图1所示放置时,菱形周长最大,
设这时菱形的边长为xcm,
由勾股定理:x2=(18﹣x)2+62,
解得:x=10,
∴4x=40,
即菱形的最大周长为40cm.
当两张纸条如图所2示放置时,即是正方形时取得最小值为:4×6=24.
∴菱形周长的最大值与最小值的和是40﹣24=16,
故答案为:16.
11.解:延长BG,交AE与点C,
∵∠ABC=45°
∴△ABC是等腰直角三角形,
∴AB=AC
∴CE=5
∵△CED是等腰直角三角形,
∴CD=5
∵CD=GF,
∴中间的小正方形的边长是5,因而周长是20.
故答案为20
12.解:连接BP,
(cm2),
∴AB=BC==3(cm),
∴(cm2),
∴,
∴(cm),
故答案为:2.
13.解:连接BD交AC于O,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC=×6=3,
∵AB=5,
由勾股定理得:OB=4,
∴BD=2OB=8,
∵AB∥CD,
∴△EAB和△ECD的高的和等于点C到直线AB的距离,
∴△EAB和△ECD的面积和=×菱形ABCD的面积=×==12.
故答案为:12
14.解:在正方形ABCD中,
AD=CD,∠ADC=∠DCN=90°,
在△ADM与△DCN中,
,
∴△ADM≌△DCN(SAS),
∴∠DAM=∠CDN,∠DMA=∠CND,
∵∠DAM+∠AMD=90°,
∴∠PDM+∠DMP=90°,
∴∠DPM=90°,
∵∠DPM=∠APN,
∴△ANP为直角三角形,
∴AN为直角三角形的斜边,由直角三角形的性质得PQ=AN,
∵DM=CN=2,BC=CD=AB=8,
∴BN=BC﹣CN=6,
在△ANB中,AN===10,
∴PQ=5.
故答案为:5..
15.解:连接OP,
∵四边形ABCD是菱形,
∴AC⊥BD,AO=AC=10,BD=BD=5,
∴AB==5,
∵PE⊥OA于点E,PF⊥OB于点F,
∴∠EOF=∠OEP=∠OFP=90°,
∴四边形OEPF是矩形,
∴EF=OP,
∵当OP取最小值时,EF的值最小,
∴当OP⊥AB时,OP最小,
∴S△ABO=OA OB=AB OP,
∴OP==2,
∴EF的最小值为2,
故答案为:2.
16.解:连接AM,延长AM交CD于G,连接FG,
∵四边形ABCD是正方形,
∴AB=CD=BC=2,AB∥CD,∠C=90°,
∴∠AEM=∠GDM,∠EAM=∠DGM,
∵M为DE的中点,
∴ME=MD,
在△AEM和GDM中,
,
∴△AEM≌△GDM(AAS),
∴AM=MG,AE=DG=AB=CD,
∴CG=CD=,
∵点N为AF的中点,
∴MN=FG,
∵F为BC的中点,
∴CF=BC=,
∴FG==2,
∴MN=1,
故答案为:1.
三.解答题(共7小题,满分56分)
17.证明:作EM⊥AF于M,连接EF,
∵∠B=90°,
∴∠B=∠AME=90°,
∵∠1=∠2,
∴BE=EM,
在Rt△ABE与Rt△AME中,
,
∴Rt△ABE≌Rt△AME(HL),
∴AM=AB=BC,EM=BE,
∵E是BC中点,
∴EC=BE=EM,
在Rt△EMF与Rt△ECF中,
,
∴Rt△EMF≌Rt△ECF(HL),
∴FM=FC,
∵AF=AM+MF,
∴AF=BC+CF.
18.(1)证明:∵正方形ABCD,
∴AD=DC=AB=BC,∠C=∠D=∠BAD=90°,AB∥CD,
∵AF⊥BE,
∴∠AOE=90°,
∴∠EAF+∠AEB=90°,∠EAF+∠BAF=90°,
∴∠AEB=∠BAF,
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AEB=∠AFD,
∵∠BAD=∠D,AB=AD,
∴△BAE≌△ADF,
∴AE=DF,
∵E为AD边上的中点,
∴点F是CD边的中点;
(2)证明:延长AD到G.使MG=MB.连接FG,FB,
∵BM=DM+CD,
∴DG=DC=BC,
∵∠GDF=∠C=90°,DF=CF,
∴△FDG≌△FCB(SAS),
∴∠DFG=∠CFB,
∴B,F,G共线,
∵E为AD边上的中点,点F是CD边的中点,AD=CD
∴AE=CF,
∵AB=BC,∠C=∠BAD=90°,AE=CF,
∴△ABE≌△CBF,
∴∠ABE=∠CBF,
∵AG∥BC,
∴∠AGB=∠CBF=∠ABE,
∴∠MBC=∠AMB=2∠AGB=2∠GBC=2∠ABE,
∴∠MBC=2∠ABE.
19.(1)证明:如图,连接BF,在矩形ABCD中,AD=BC,∠ADC=∠BCD=90°,
∵F为DE的中点,
∴CF=DF,
∴∠CDF=∠DCF,
∴∠ADC+∠CDF=∠BCD+∠DCF,
即∠ADF=∠BCF,
在△ADF和△BCF中,
,
∴△ADF≌△BCF(SAS),
∴∠AFD=∠BFC,
∵BE=BD,F为DE的中点,
∴BF⊥DE,
∴∠AFC=∠AFB+∠BFC=∠AFB+∠AFD=90°,
∴CF⊥AF;
(2)解:∵△ADF≌△BCF,
∴点F到AD、BC的距离相等,
∵AB=10cm,
∴点F到AD的距离为×10=5cm,
∴△ADF的面积=×16×5=40cm2.
20.证明:(1)∵AD=CD,点E是边AC的中点,
∴DE⊥AC.
即得DE是线段AC的垂直平分线.
∴AF=CF.
∴∠FAC=∠ACB.
在Rt△ABC中,由∠BAC=90°,
得∠B+∠ACB=90°,∠FAC+∠BAF=90°.
∴∠B=∠BAF.
∴AF=BF.
(2)∵AG∥CF,∴∠AGE=∠CFE.
又∵点E是边AC的中点,∴AE=CE.
在△AEG和△CEF中,
,
∴△AEG≌△CEF(AAS).
∴AG=CF.
又∵AG∥CF,∴四边形AFCG是平行四边形.
∵AF=CF,∴四边形AFCG是菱形.
在Rt△ABC中,由AF=CF,AF=BF,得BF=CF.
即得点F是边BC的中点.
又∵AB=AC,∴AF⊥BC.即得∠AFC=90°.
∴四边形AFCG是正方形.
21.解:(1)结论:DN+BM=CF.
理由:如图1中,
∵四边形ABCD是正方形,
∴AD=AB=BC,AB∥CD,∠B=∠DAE=90°,
∵∠ADE=∠BAF,
∴△DAE≌△BAF(ASA),
∴AE=BF,
∵BA=BC,
∴BE=CF,
∵EM∥DN,DE∥MN,
∴四边形MNDE是平行四边形,
∴DN=EN,
∴DN+BM=EN+BM=BE=CF.
(2)①如图2中,连接CQ交AD于T.
由翻折的性质可知,CQ⊥MN,
∵∠BAF+∠DAF=90°,∠ADE=∠BAF,
∴∠ADE+∠DAF=90°,
∴∠AOD=90°,
∴AF⊥DE,
∵MN∥DE,
∴MN⊥AF,
∴CQ∥AF,
∵AT∥CF,
∴四边形AFCT是平行四边形,
∴AT=CF=4﹣1=3,
∴DT=AD﹣AT=1,
∴点Q的运动轨迹是射线CQ,当AQ⊥CQ时,AQ的值最小,
在Rt△ABF中,AF===,
∵AF∥CQAQ⊥CQ,
∴AQ⊥AF,
∴∠QAF=∠BAD=90°,
∴∠QAT=∠BAF,
∵∠AQT=∠B=90°,
∴AQ=,
∴AQ的最小值为.
②如图3中,连接MF.
∵线段PQ恰好经过点A,由翻折的性质可知,GA=FG,
∵MN⊥AF,
∴MA=MF,
设MA=MF=x,
在Rt△BFM中 BM2+BF2=MF2,
∴(4﹣x)2+12=x2,
∴x=,
∵AE=BF=1,
∴EM=AM﹣AE=﹣1=,
∴DE的平移距离为.
22.解:(1)连接BN,过N作NH⊥BC于H,如图1所示,
∵正方形ABCD,N为AC中点,
∴△ANB与△BHN都为等腰直角三角形,
∴AN=BN=AB=2,NH=CH=BN=2,
在Rt△BNM中,由勾股定理得:BM===,
在Rt△NHE中,NH=2,HE=2﹣1=1,EN==,
则BM+EN=+;
(2)∵正方形ABCD,M为AC中点,
∴BM=AM=CM=2,
∵MN=,
∴CN=CM﹣MN=,
若过N作NE′⊥BC于点E′,如图2所示,则得到NE′=CE′=1,
∴E′与E重合,且NE=NE′=1,
∴BM+EN=2+1;
(3)ME+EN的最小值为,理由为:
如图3所示,作出点E关于AC的对称点E′,则CE′=CE=1,
将MN平移至E′F处,则四边形MNE′F为平行四边形,
连接BF,EF,过F作FG⊥CD于G,可得△E′FG为等腰直角三角形,
∴E′F=MN=,FG=E′G=1=CE,
∴四边形CEFG为矩形,
∴EF=CG=2,BE=BC﹣CE=3,
∴BF==,
显然,BM+EN=BM+E′N=BM+FM≥BF=.
23.解:(1)结论:MN=AM+CN.
理由:如图1中,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∵四边形ABCD是正方形,
∴∠A=∠BCD=∠ABC=∠BCM′=90°,
∴∠NCM′=180°,
∴N,C,M′共线,
∵∠ABM=∠CBM′,
∴∠MBM′=∠ABC=90°,
∵∠MBN=45°,
∴∠MBN=∠M′BN=45°,
在△BNM和△BNM′中,
,
∴△NBM≌△NBM′(SAS),
∴MN=NM′,
∵AM=CM′,
∴MN=AM+CN.
故答案为:MN=AM+CN;
(2)结论:MN=AM+CN.
理由:如图2中,把△ABM绕点B顺时针旋转使AB边与BC边重合,则△ABM≌△CBM′,
∵BC∥AD,AB=BC=CD,
∴梯形ABCD是等腰梯形,
∴∠A+∠BCD=180°,
∴AM=CM′,BM=BM′,∠A=∠BCM′,∠ABM=∠M′BC,
∴∠BCM′+∠BCD=180°,
∴点M′、C、N三点共线,
∵∠MBN=∠ABC,
∴∠M′BN=∠M′BC+∠CBN=∠ABM+∠CBN=∠ABC﹣∠MBN=∠ABC,
∴∠MBN=∠M′BN,
在△BMN和△BM′N中,
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N,
又∵M′N=CM′+CN=AM+CN,
∴MN=AM+CN;
(3)结论:MN=CN﹣AM.
理由:如图3中,作∠CBM′=∠ABM交CN于点M′,
∵∠ABC+∠ADC=180°,
∴∠BAD+∠C=360°﹣180°=180°,
又∵∠BAD+∠BAM=180°,
∴∠C=∠BAM,
在△ABM和△CBM′中,
,
∴△ABM≌△CBM′(ASA),
∴AM=CM′,BM=BM′,
∵∠MBN=∠ABC,
∴∠M′BN=∠ABC﹣(∠ABN+∠CBM′)=∠ABC﹣(∠ABN+∠ABM)=∠ABC﹣∠MBN=∠ABC,
∴∠MBN=∠M′BN,
在△MBN和△M′BN中,
,
∴△MBN≌△M′BN(SAS),
∴MN=M′N,
∵M′N=CN﹣CM′=CN﹣AM,
∴MN=CN﹣AM.
故答案为:MN=CN﹣AM.
