2021-2022学年冀教版数学七年级下册6.3二元一次方程组的应用课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版数学七年级下册6.3二元一次方程组的应用课时练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 313.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-22 00:00:00 | ||
图片预览





文档简介
二元一次方程组的应用
一、单选题
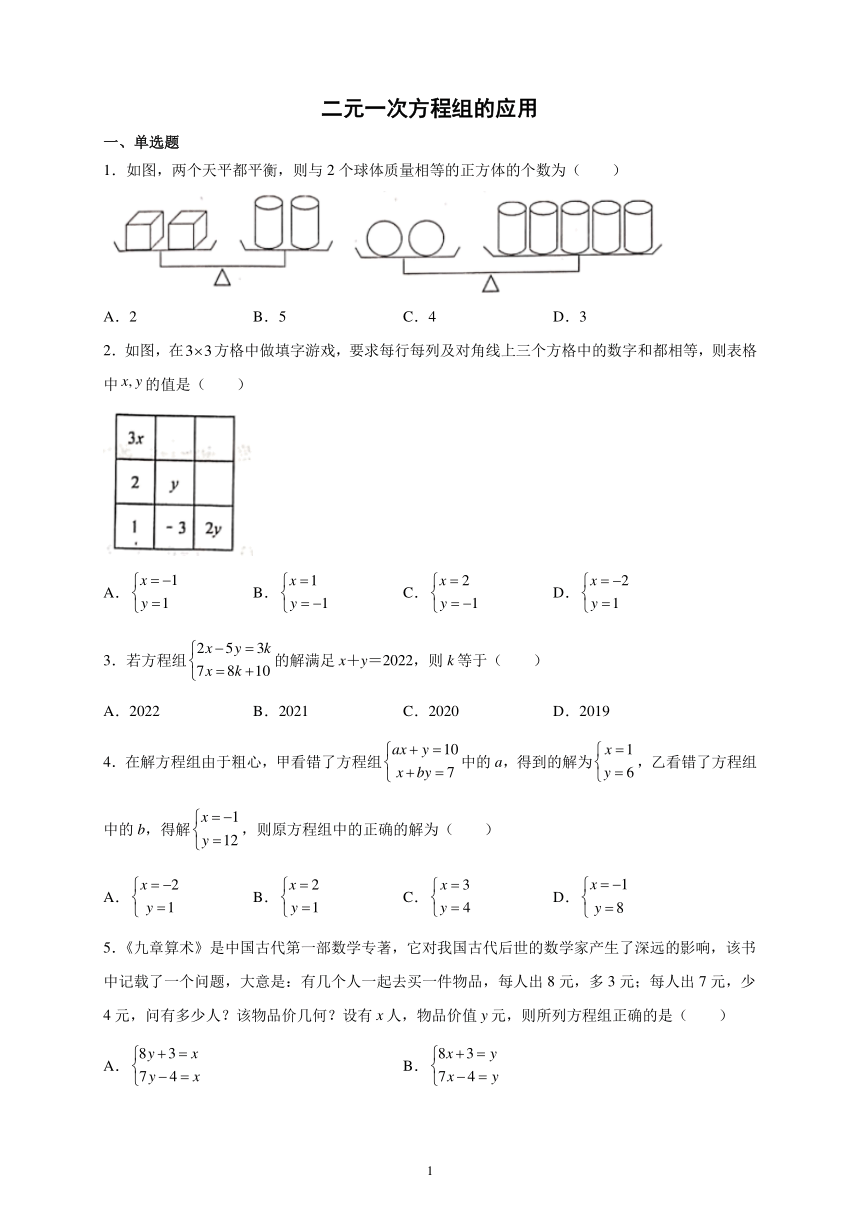
1.如图,两个天平都平衡,则与2个球体质量相等的正方体的个数为( )
A.2 B.5 C.4 D.3
2.如图,在方格中做填字游戏,要求每行每列及对角线上三个方格中的数字和都相等,则表格中的值是( )
A. B. C. D.
3.若方程组的解满足x+y=2022,则k等于( )
A.2022 B.2021 C.2020 D.2019
4.在解方程组由于粗心,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得解,则原方程组中的正确的解为( )
A. B. C. D.
5.《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是( )
A. B.
C. D.
6.如图,一个长方形图案是由8个大小相同的小长方形拼成,宽为,设每个小长方形的长为,宽为,根据题意可列方程组为( )
A. B. C. D.
7.某学校操场是周长为400 m 的长方形,且长比宽的2倍少40m.若设该长方形的长为 x,宽为y,则可列方程组为( )
A. B. C. D.
8.有大小两个盛酒的捅,已知个大桶和个小桶可以盛酒斛(斛,古代一种容器单位).个大桶和个小桶盛酒斛,设个大桶盛酒斛,个小桶酒斛,可列方程组为( )
A. B. C. D.
9.社区李主任要用600元钱购买一次性防护服和医用洗手液两种防疫用品,一次性防护服每套40元,医用洗手液每瓶30元,李主任的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
10.小明郊游时,早上9时下车,先走平路然后登山,到山顶后又沿原路返回到下车处,正好是下午2时.若他走平路每小时行4km,爬山时每小时走3km,下山时每小时走6km,小明从上午到下午一共走的路程是( )
A.5km B.10km C.20km D.答案不唯一
11.甲、乙两个工人按计划一个月应生产680个零件,结果甲超额完成计划的20%,乙超额完成计划的15%,两人一共多生产118个零件,则原计划甲、乙各生产零件数为( )
A.320,360 B.360,320 C.300,380 D.380,380
12.小华告诉小明:我生日的月数和日数之和为24,且日数恰好是月数的7倍,你猜我的生日是哪天?小华的生日应该是( )
A.3月21日 B.2月14日 C.8月16日 D.4月24日
13.佳佳坐在匀速行驶的车上,将每隔一段时间看到的里程碑上的数描述如下:
时刻 12:00 13:00 14:00
里程碑上的数 是一个两位数,数字之和为7 十位数字和个位数字与12:00时看到的刚好相反 比12:00看到的两位数中间多了个0
则12:00时看到的两位数是( )A.16 B.25 C.34 D.52
14.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
15.有支队名运动员参加篮球、排球比赛,其中每支篮球队人,每支排球队人,每名运动员只能参加一项比赛.设篮球队有支参赛,排球队有参赛,则下面所列方程组正确的是( )
A. B.
C. D.
二、填空题
16.已知关于x,y的二元一次方程组的解满足x+y=0,则m的值为__.
17.某工厂去年的利润(总收入总支出)为200万元.今年总收入比去年增加了,总支出比去年减少了,今年的利润为780万元.设去年的总收入为万元、总支出为万元,根据题意可列方程组___.
18.塑料凳子轻便实用,人们生活中随处可见.如图,3 支塑料凳子叠放在一起的高度为55cm,5 支塑料凳子叠放在一起的高度为 65cm,当有 10 支塑料凳子整齐地叠放在一起时,其高度是___cm.
19.学校计划用200元钱购买A,B两种奖品,A奖品每个15元,B奖品每个25元,两种都要买且钱全部用完,则购买方案有 ___种.
20.一个两位数的十位数字与个位数字的和为8,若把这个两位数加上18,正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数,设十位数字为x,个位数字为y.则列出方程组______.
三、解答题
21.如果方程组的解中,x与y互为相反数,求x,y,m的值.
22.六年级学生若干人报名参加课外活动小组,男女生人数之比为4:3,后来又报了15名女生,这时女生人数恰好是男生人数的2倍,求最初报名时男生与女生各有多少人?
23.《九章算术》中有一道题的条件是:“今有大器五小器一容三斛,大器一小器五容二斜”大致意思是,有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,问:1大桶加1小桶共盛多少斛米?(注:斛是古代一种容量单位)
24.新世纪中学在第六届艺术节组织开展了庆祝建党100周年各项比赛活动.已知六年级(1)班和(2)班各有34人,两个班各有一部分同学参加了活动,其中(1)班参加人数的2倍比(2)班没参加的人数多3人,而(2)班参加的人数比(1)班没参加的人数的一半多5人.求这两个班各有多少人参加了艺术节活动?
25.某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售件数),如表是甲、乙两位职工某月的工资情况.
职工 甲 乙
月销售件数(件) 200 180
月工资(元) 1800 1700
(1)求职工的月基本保障工资和销售每件产品的奖励金额各是多少元?(用二元一次方程组解决问题)
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
试卷第1页,共3页
参考答案:
1.B
解:设球体、圆柱体与正方体的质量分别为x、y、z,根据已知条件,得:
,
①×2-②×5,得:
,
即2个球体相等质量的正方体的个数为5.
故选:B.
2.A
解:由题意得:,
解得:,
故答案为:A.
3.C
解:
①-②得:.
∴.
把代入x+y=2022中得:
∴k=2020.
故选C.
4.C
解:将代入,将代入,
得,
,
原方程组为
解得,
故选:C.
5.D
解:设有x人,物品价值y元,由题意得:
,
故选:D.
6.A
解:由题意可得,大长方形的宽是x与y的和
∴x+y=60
又∵小长方形的长是宽的3倍
∴x=3y
∴方程组为:
故选A.
7.C
解:若设该长方形的长为 x,宽为y,则可列方程组为,
故选:C.
8.C
解:设个大桶盛酒斛,个小桶酒斛,由题意得
,
故选C.
9.B
解:设购买一次性防护服x套,医用洗手液y瓶,依题意可得40x+30y=600
解得其正整数解为,,,
故李主任的购买方案共有4种
故选B.
10.C
解:设平路有xkm,山路有ykm.
则,
解,得x+y=10,
∴2(x+y)=20,
故选:C.
11.A
解:设原计划甲生产x个零件,乙生产y个零件,
根据题意得:,
解得:,即原计划甲生产320个零件,乙生产360个零件.
故选:A.
12.A
解:设小华同学生日的月数为x,日数为y,
依题意,得:,
解得:,
∴3月21日.
故选:A.
13.A
解:设小明12:00看到的两位数,十位数为x,个位数为y,
由题意列方程组得:,
解得:,
∴12:00时看到的两位数是16.
故选:A.
14.C
解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
15.C
解:设篮球队有支参赛,排球队有参赛,根据题意得:
,
故选:C.
16.1
解:解原方程组可化为:,
①-②得,
y=2,
把y=2,代入②得x=-2,
把y=2,x=-2代入2x+y=1-3m,
得2×(-2)+2=1-3m,
解得m=1,
故答案为:1.
17.
解:设去年的总收入为万元、总支出为万元,
由题意得,.
故答案为:.
18.90
解:设塑料凳子厚度为x(cm),凳子腿高为y(cm)
由题意可得 ,
解得: ,
则10支塑料凳子整齐叠放在一起的高度为cm.
故答案为:90.
19.2
解:设购买A奖品x个,B奖品y个.
根据题意可知:
化简得:
解得
由题意x和y均为正整数,因此x只可以为5或10
解得或
综上,共有2种购买方案.
故答案为:2
20.
解:设这个两位数的个位数字为x,十位数字为y,
根据题意得:
故答案为:
21.,,
解:因为x与y互为相反数,可得y=-x,
所以方程组上式可化为,
①,
方程组下式可化为,
②,
联立①②解得:,.
所以.
22.最初报名时男生有12人,女生有9人.
解:设最初报名时女生有x人,男生有y人,
依题意,得:,
解得:,
答:最初报名时男生有12人,女生有9人.
23.1大桶加1小桶共盛斛米.
解:设1个大桶可以盛x斛米,一个小桶可以盛y斛米,
由题意可得,
解得:x+y=,
答:1大桶加1小桶共盛斛米.
24.六年级(1)班参加人数为10人,(2)班参加人数为17人
解:设六年级(1)班参加人数为x人,(2)班参加人数为y人,
由题意得
,
解得.
答:六年级(1)班参加人数为10人,(2)班参加人数为17人.
25.(1)800,5 (2)240
解:(1)
设职工的月基本保障工资为x元,销售每件产品的奖励金额为y元,
根据题意得: ,
解得: .
答:职工的月基本保障工资为800元,销售每件产品的奖励金额为5元.
(2)
(2000-800)÷5=240(件).
答:丙该月销售了240件产品.
答案第1页,共2页
一、单选题
1.如图,两个天平都平衡,则与2个球体质量相等的正方体的个数为( )
A.2 B.5 C.4 D.3
2.如图,在方格中做填字游戏,要求每行每列及对角线上三个方格中的数字和都相等,则表格中的值是( )
A. B. C. D.
3.若方程组的解满足x+y=2022,则k等于( )
A.2022 B.2021 C.2020 D.2019
4.在解方程组由于粗心,甲看错了方程组中的a,得到的解为,乙看错了方程组中的b,得解,则原方程组中的正确的解为( )
A. B. C. D.
5.《九章算术》是中国古代第一部数学专著,它对我国古代后世的数学家产生了深远的影响,该书中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x人,物品价值y元,则所列方程组正确的是( )
A. B.
C. D.
6.如图,一个长方形图案是由8个大小相同的小长方形拼成,宽为,设每个小长方形的长为,宽为,根据题意可列方程组为( )
A. B. C. D.
7.某学校操场是周长为400 m 的长方形,且长比宽的2倍少40m.若设该长方形的长为 x,宽为y,则可列方程组为( )
A. B. C. D.
8.有大小两个盛酒的捅,已知个大桶和个小桶可以盛酒斛(斛,古代一种容器单位).个大桶和个小桶盛酒斛,设个大桶盛酒斛,个小桶酒斛,可列方程组为( )
A. B. C. D.
9.社区李主任要用600元钱购买一次性防护服和医用洗手液两种防疫用品,一次性防护服每套40元,医用洗手液每瓶30元,李主任的购买方案共有( )
A.3种 B.4种 C.5种 D.6种
10.小明郊游时,早上9时下车,先走平路然后登山,到山顶后又沿原路返回到下车处,正好是下午2时.若他走平路每小时行4km,爬山时每小时走3km,下山时每小时走6km,小明从上午到下午一共走的路程是( )
A.5km B.10km C.20km D.答案不唯一
11.甲、乙两个工人按计划一个月应生产680个零件,结果甲超额完成计划的20%,乙超额完成计划的15%,两人一共多生产118个零件,则原计划甲、乙各生产零件数为( )
A.320,360 B.360,320 C.300,380 D.380,380
12.小华告诉小明:我生日的月数和日数之和为24,且日数恰好是月数的7倍,你猜我的生日是哪天?小华的生日应该是( )
A.3月21日 B.2月14日 C.8月16日 D.4月24日
13.佳佳坐在匀速行驶的车上,将每隔一段时间看到的里程碑上的数描述如下:
时刻 12:00 13:00 14:00
里程碑上的数 是一个两位数,数字之和为7 十位数字和个位数字与12:00时看到的刚好相反 比12:00看到的两位数中间多了个0
则12:00时看到的两位数是( )A.16 B.25 C.34 D.52
14.甲是乙现在的年龄时,乙8岁;乙是甲现在年龄时,甲20岁,则( )
A.甲比乙大6岁 B.乙比甲大6岁
C.甲比乙大4岁 D.乙比甲大4岁
15.有支队名运动员参加篮球、排球比赛,其中每支篮球队人,每支排球队人,每名运动员只能参加一项比赛.设篮球队有支参赛,排球队有参赛,则下面所列方程组正确的是( )
A. B.
C. D.
二、填空题
16.已知关于x,y的二元一次方程组的解满足x+y=0,则m的值为__.
17.某工厂去年的利润(总收入总支出)为200万元.今年总收入比去年增加了,总支出比去年减少了,今年的利润为780万元.设去年的总收入为万元、总支出为万元,根据题意可列方程组___.
18.塑料凳子轻便实用,人们生活中随处可见.如图,3 支塑料凳子叠放在一起的高度为55cm,5 支塑料凳子叠放在一起的高度为 65cm,当有 10 支塑料凳子整齐地叠放在一起时,其高度是___cm.
19.学校计划用200元钱购买A,B两种奖品,A奖品每个15元,B奖品每个25元,两种都要买且钱全部用完,则购买方案有 ___种.
20.一个两位数的十位数字与个位数字的和为8,若把这个两位数加上18,正好等于将这个两位数的十位数字与个位数字对调后所组成的新两位数,设十位数字为x,个位数字为y.则列出方程组______.
三、解答题
21.如果方程组的解中,x与y互为相反数,求x,y,m的值.
22.六年级学生若干人报名参加课外活动小组,男女生人数之比为4:3,后来又报了15名女生,这时女生人数恰好是男生人数的2倍,求最初报名时男生与女生各有多少人?
23.《九章算术》中有一道题的条件是:“今有大器五小器一容三斛,大器一小器五容二斜”大致意思是,有大小两种盛米的桶,5大桶加1小桶共盛3斛米,1大桶加5小桶共盛2斛米,问:1大桶加1小桶共盛多少斛米?(注:斛是古代一种容量单位)
24.新世纪中学在第六届艺术节组织开展了庆祝建党100周年各项比赛活动.已知六年级(1)班和(2)班各有34人,两个班各有一部分同学参加了活动,其中(1)班参加人数的2倍比(2)班没参加的人数多3人,而(2)班参加的人数比(1)班没参加的人数的一半多5人.求这两个班各有多少人参加了艺术节活动?
25.某玻璃制品销售公司职工的月工资由基本保障工资和计件奖励工资两部分组成(计件奖励工资=销售每件的奖励金额×销售件数),如表是甲、乙两位职工某月的工资情况.
职工 甲 乙
月销售件数(件) 200 180
月工资(元) 1800 1700
(1)求职工的月基本保障工资和销售每件产品的奖励金额各是多少元?(用二元一次方程组解决问题)
(2)若职工丙今年5月份的工资为2000元,那么丙该月销售了多少件产品?
试卷第1页,共3页
参考答案:
1.B
解:设球体、圆柱体与正方体的质量分别为x、y、z,根据已知条件,得:
,
①×2-②×5,得:
,
即2个球体相等质量的正方体的个数为5.
故选:B.
2.A
解:由题意得:,
解得:,
故答案为:A.
3.C
解:
①-②得:.
∴.
把代入x+y=2022中得:
∴k=2020.
故选C.
4.C
解:将代入,将代入,
得,
,
原方程组为
解得,
故选:C.
5.D
解:设有x人,物品价值y元,由题意得:
,
故选:D.
6.A
解:由题意可得,大长方形的宽是x与y的和
∴x+y=60
又∵小长方形的长是宽的3倍
∴x=3y
∴方程组为:
故选A.
7.C
解:若设该长方形的长为 x,宽为y,则可列方程组为,
故选:C.
8.C
解:设个大桶盛酒斛,个小桶酒斛,由题意得
,
故选C.
9.B
解:设购买一次性防护服x套,医用洗手液y瓶,依题意可得40x+30y=600
解得其正整数解为,,,
故李主任的购买方案共有4种
故选B.
10.C
解:设平路有xkm,山路有ykm.
则,
解,得x+y=10,
∴2(x+y)=20,
故选:C.
11.A
解:设原计划甲生产x个零件,乙生产y个零件,
根据题意得:,
解得:,即原计划甲生产320个零件,乙生产360个零件.
故选:A.
12.A
解:设小华同学生日的月数为x,日数为y,
依题意,得:,
解得:,
∴3月21日.
故选:A.
13.A
解:设小明12:00看到的两位数,十位数为x,个位数为y,
由题意列方程组得:,
解得:,
∴12:00时看到的两位数是16.
故选:A.
14.C
解:设甲现在x岁,乙现在y岁.
根据题意,得,
解得,
∴
故选:C
15.C
解:设篮球队有支参赛,排球队有参赛,根据题意得:
,
故选:C.
16.1
解:解原方程组可化为:,
①-②得,
y=2,
把y=2,代入②得x=-2,
把y=2,x=-2代入2x+y=1-3m,
得2×(-2)+2=1-3m,
解得m=1,
故答案为:1.
17.
解:设去年的总收入为万元、总支出为万元,
由题意得,.
故答案为:.
18.90
解:设塑料凳子厚度为x(cm),凳子腿高为y(cm)
由题意可得 ,
解得: ,
则10支塑料凳子整齐叠放在一起的高度为cm.
故答案为:90.
19.2
解:设购买A奖品x个,B奖品y个.
根据题意可知:
化简得:
解得
由题意x和y均为正整数,因此x只可以为5或10
解得或
综上,共有2种购买方案.
故答案为:2
20.
解:设这个两位数的个位数字为x,十位数字为y,
根据题意得:
故答案为:
21.,,
解:因为x与y互为相反数,可得y=-x,
所以方程组上式可化为,
①,
方程组下式可化为,
②,
联立①②解得:,.
所以.
22.最初报名时男生有12人,女生有9人.
解:设最初报名时女生有x人,男生有y人,
依题意,得:,
解得:,
答:最初报名时男生有12人,女生有9人.
23.1大桶加1小桶共盛斛米.
解:设1个大桶可以盛x斛米,一个小桶可以盛y斛米,
由题意可得,
解得:x+y=,
答:1大桶加1小桶共盛斛米.
24.六年级(1)班参加人数为10人,(2)班参加人数为17人
解:设六年级(1)班参加人数为x人,(2)班参加人数为y人,
由题意得
,
解得.
答:六年级(1)班参加人数为10人,(2)班参加人数为17人.
25.(1)800,5 (2)240
解:(1)
设职工的月基本保障工资为x元,销售每件产品的奖励金额为y元,
根据题意得: ,
解得: .
答:职工的月基本保障工资为800元,销售每件产品的奖励金额为5元.
(2)
(2000-800)÷5=240(件).
答:丙该月销售了240件产品.
答案第1页,共2页
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
