2021-2022学年冀教版数学九年级下册 29.4切线长定理 课时练习(word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版数学九年级下册 29.4切线长定理 课时练习(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 540.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 00:00:00 | ||
图片预览



文档简介
切线长定理
一、单选题
1.如图,分别切于两点,切于点E,交于点.若的周长等于,则线段的长是( )
A. B.3 C. D.
2.如图,PA、PB是的切线,A、B为切点,连接OB、AB,若,则的度数为( )
A.50° B.55° C.65° D.70°
3.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
4.如图,与的两边分别相切,其中OA边与⊙C相切于点P.若,,则OC的长为( )
A.8 B. C. D.
5.如图所示,已知⊙I是△ABC的内切圆,点I是内心,若∠A=35°,则∠BIC等于( )
A.35° B.70° C.145° D.107.5°
6.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
7.如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
A. B. C.π 或 D.或
8.如图,PA与⊙O相切于点A,线段PO交⊙O于点C,过点C作⊙O的切线交PA于点B.若PC=4,AB=3,则⊙O的半径等于( )
A.4 B.5 C.6 D.12
9.如图,PA、PB、MN是⊙O的切线,A、B、C是切点,MN分别交线段PA、PB于M、N两点.若∠APB=50°,则∠MON=( )
A.50° B.60° C.65° D.70°
10.如图,锐角△ABC内接于⊙O,I为△ABC内心,已知∠OAB=50°,则∠AIB的度数为( )
A.110° B.125° C.130° D.135°
11.如图,在矩形ABCD中,,,点E、F分别是AD、BC的中点,点P在线段EF上,内切圆半径的最大值是( )
A.1 B. C. D.
12.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=31°,则∠BEC的大小为( )
A.120° B.121° C.122° D.125°
二、填空题
13.已知等腰三角形三边长分别是13、13、10,则这个等腰三角形内切圆半径为____
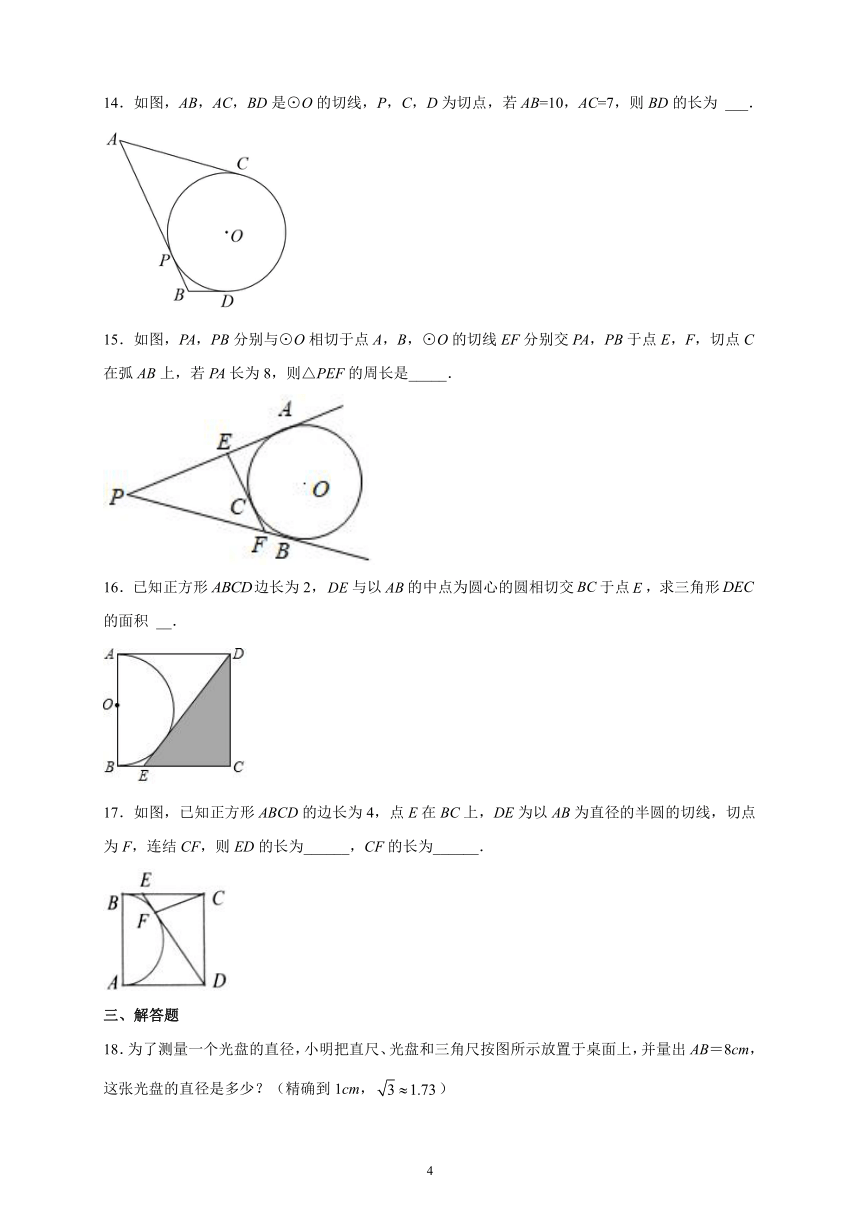
14.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,若AB=10,AC=7,则BD的长为 ___.
15.如图,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA长为8,则△PEF的周长是_____.
16.已知正方形边长为2,与以的中点为圆心的圆相切交于点,求三角形的面积 __.
17.如图,已知正方形ABCD的边长为4,点E在BC上,DE为以AB为直径的半圆的切线,切点为F,连结CF,则ED的长为______,CF的长为______.
三、解答题
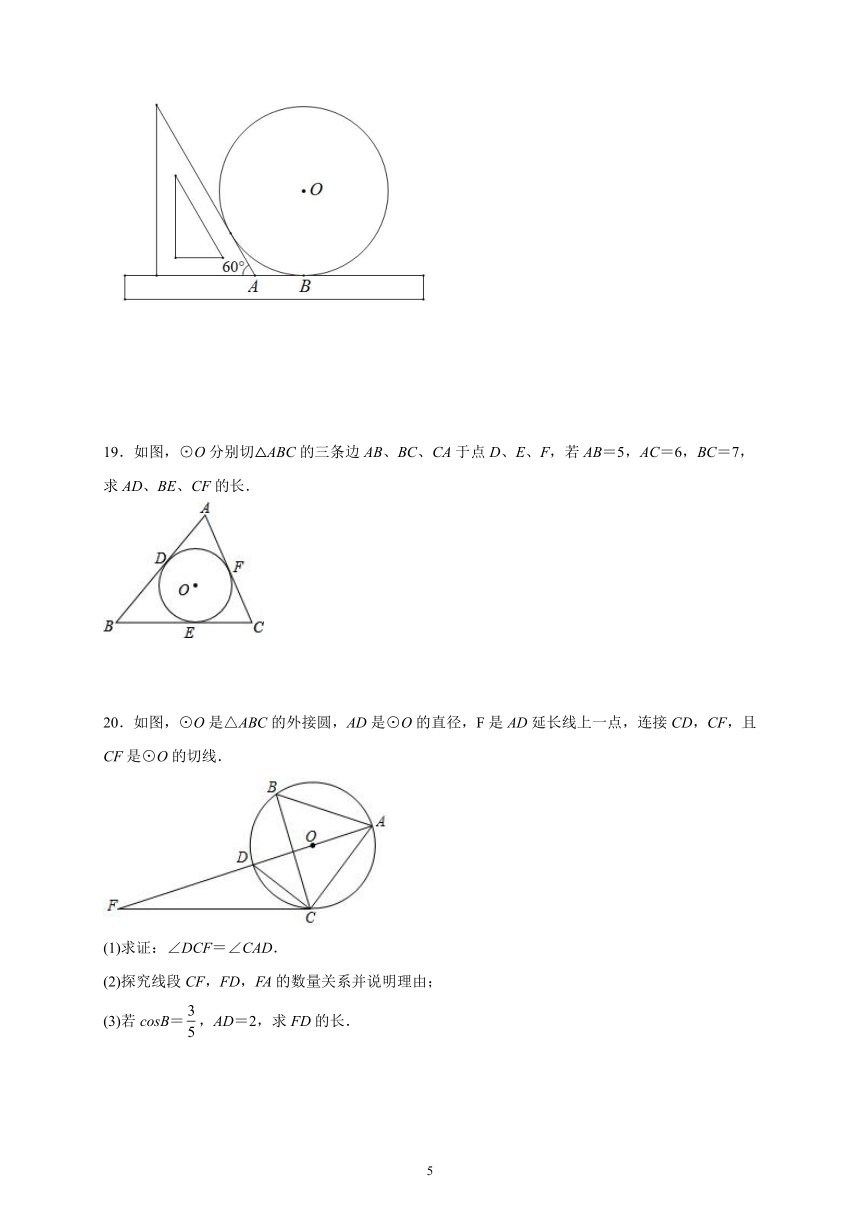
18.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=8cm,这张光盘的直径是多少?(精确到1cm,)
19.如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,若AB=5,AC=6,BC=7,求AD、BE、CF的长.
20.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且CF是⊙O的切线.
(1)求证:∠DCF=∠CAD.
(2)探究线段CF,FD,FA的数量关系并说明理由;
(3)若cosB=,AD=2,求FD的长.
21.已知AB是⊙O的直径,BD为⊙O的切线,切点为B.过⊙O上的点C作,交BD点D.连接AC,BC.
图1 图2
(1)如图①,若DC为⊙O的切线,切点为C.求∠BCD和∠DBC的大小;
(2)如图②,当CD与⊙O交于点E时,连接BE.若∠EBD=30°,求∠BCD和∠DBC的大小.
试卷第1页,共3页
参考答案:
1.A
解:,切于、两点,切于点,交,于,,
,,,
的周长等于,
,
,
故选:A.
2.A
解:∵PA、PB是⊙O的切线,
∴PA=PB,∠OBP=90°,
又∵∠ABO=25°,
∴∠PBA=90°-25°=65°=∠PAB,
∴∠P=180°-65°-65°=50°,
故选:A.
3.C
解:∵PA,PB为⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△APB为等边三角形,
∴AB=PA=5.
故选:C.
4.C
解:如图所示,连接CP,
∵OA,OB都是圆C的切线,∠AOB=90°,P为切点,
∴∠CPO=90°,∠COP=45°,
∴∠PCO=∠COP=45°,
∴CP=OP=4,
∴,
故选C.
5.D
解:∵∠A=35°,
∴
∵点I是的内心,
∴
即
∠BIC 107.5°
故选D
6.B
解: ∵∠C=90°,AC=12,BC=5,
∴AB===13,
∵⊙O与Rt△ABC的三边相切于点D、E、F,
,
设,则,
即
解得
故选:B.
7.D
解:如图1,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,
连接WE,WF,CW,OC,OW,则四边形OCFW是矩形,
∴OW=CF,WF=1,
∵∠ACB=60○,
∴∠WCF=∠ACB=30°,
所以点O移动的距离为OW=CF===.
如图2,当圆O滚动到圆O′位置与CA,CB相切,切点分别为F,E,
连接OO′,O′E,O′C,O′F,OC,则四边形OCEO′是矩形,
∴OO′=CE,
∵∠ACB=60○,
∴∠ACE=120○,
∴∠O′CE=60°,
∴点O移动的距离为OO′=CE===,·
故选:D.
8.C
解:设⊙O的半径为r,
由切线长定理得,BC=BA=3,
∵BC是⊙O的切线,
∴∠BCP=90°,
∴PB==5,
∴AP=PB+AB=8,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴AP2+OA2=OP2,即82+r2=(4+r)2,
解得,r=6,
故选:C.
9.C
解:连接AO,BO,OC,
∵PA、PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∵∠APB=50°,
∴∠AOB=360°-2×90°-50°=130°,
∵PA、PB、MN是⊙O的切线,
∴∠BNO=∠CNO,∠AMO=∠CMO,
∴∠BON=∠CON,AOM=∠COM,
∴∠MON=∠CON+∠COM=∠AOB=65°.
故选:C.
10.A
解:连接OB,
∵OA=OB,
∴∠OAB=∠OBA=50°,
∴∠O=180°﹣(∠OAB+∠OBA)=80°,
∴∠C=40°,
∵I为△ABC内心,
∴AI、BI为∠CAB、∠CBA的平分线,
∴,,
∴,
∴∠AIB=180°﹣(∠IAB+∠IBA)=180°﹣70°=110°.
故选:A.
11.D
解:∵点E、F分别是AD、BC的中点,四边形ABCD是矩形,
∴EF∥AB,
∵P在EF上,AB=8,BC=6,
∴S△PAB=×8×3=12,
设△PAB内切圆半径是r,
∵S△PAB=(AP+PB+AB) r=12,
∴AP+BP最小时,r有最大值,
如图,F是BC的中点,所以点B关于EF的对称点是C点,连接CA与EF交于点P',
∵AP+BP=AP+CP≥CA,
∴此时CA即为AP+BP最小值,
∵AB=8,AD=6,
∴AC==10,
∴AP+BP最小值为10,
∴PA=PB=5,
∴×5×r+×5×r+×8×r=12,
解得r=,
故选:D.
12.B
解:在⊙O中,∠CBD=31°,
∴∠CAD=31°,
∵点E是△ABC的内心,
∴∠BAC=2∠CAD=62°,
∴∠EBC+∠ECB=(180°-62°)÷2=59°,
∴∠BEC=180°-59°=121°.
故选:B.
13.
解:等腰△ABC中,AB=AC,AD为BC边上的高,故AD为BC边上的中线,即BD=DC,
在直角△ABD中,AB=13,BD=5,
∴AD==12,
则S△ABC=×10×12=60.
∵S△ABC=(13+13+10)r,
∴内切圆的半径r=,
故答案为:.
14.
解:∵AC与⊙O相切于点C、AB与⊙O相切于点P,
∴AC=AP=7,
∵AB=10,
∴BP=AB-AP=10-7=3,
∵BD与⊙O相切于点D、BP与⊙O相切于点P,
∴BD=BP=3,
∴BD的长为3,
故答案为:3.
15.16
解:∵PA、PB、EF分别与⊙O相切于点A、B、C,
∴AE=CE,FB=CF,PA=PB=8,
∴△PEF的周长=PE+EF+PF=PA+PB=16.
故答案为:16.
16.
解:设与圆相切于点,
四边形是正方形,
,,
、是圆的半径,
与圆相切于点,与圆相切于点,
,,
设,
则,,
∵在中,,
,
解得:,
,
三角形的面积,
故答案为:1.5.
17. 5 ##
解:∵正方形ABCD
∴CD=AD=BC=4,CE⊥AB,DA⊥AB
∵以AB为直径的半圆
∴BE、AD也是半圆的切线
∵DE为以AB为直径的半圆的切线,
∴EB=EF、DA=DF=4
∴EC=BC-BE=4-EF,DE=DF+EF=4+EF
在Rt△DCE中,
∴
解得
∴DE=DF+EF=4+EF=5
过F作FG⊥DC于G,如图
∴
∴
∴
解得
∴
∴在Rt△CFG中,
故答案为:5,
18.28 cm
解:设光盘的圆心为O,连接OC,OB,OA,如图所示:
∵AC,AB分别为圆O的切线,
∴OC⊥AC,OB⊥AB,
∵OC,OB都是圆O的半径
∴OC=OB
∴AO为∠CAB的平分线,
∵∠CAD=60°,∠CAD+∠CAB=180°
∴∠CAB=180°-∠CAD=120°
∴∠OAC=∠OAB=∠CAB=60°,
在Rt△AOB中,∠OBA=90°,∠OAB=60°,AB=8cm,
∴tan∠OAB=tan60°=,即=,
∴OB=8cm,
则光盘的直径为16≈28 cm.
故答案为:28 cm
19.AD=2,BE=3,CF=4
解:∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,
∴AD=AF,BD=BE,CE=CF,
可设AD=AF=x,BD=BE=y,CE=CF=z,
∵AB=5,AC=6,BC=7,
∴AD+BD=5,AF+CF=6,BE+CE=7,
∴x+y=5①,x+z=6②,y+z=7③,
由①+②+③,得:x+y+z=9④,
由④-①,得:z=4,
把z=4分别代入②,③得:x=2,y=3,
即AD=2,BE=3,CF=4.
20.(1)证明过程见详解 (2)FC2=FD FA;理由见详解 (3)
(1)
证明:如图,连接OC,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠OCD+∠OCA=90°,
∵FC是⊙O的切线,
∴∠DCF+∠OCD=90°,
∴∠OCA=∠DCF,
∵OC=OA,
∴∠CAD=∠OCA,
∴∠DCF=∠CAD;
(2)
解:FC2=FD FA,理由如下:
∵∠FCD=∠FAC,∠F=∠F,
∴△FCD∽△FAC,
∴,
∴FC2=FD FA;
(3)
解:∵∠B=∠ADC,cosB=,
∴cos∠ADC=,
在Rt△ACD中,
∵cos∠ADC==,
∴,
由(2)知△FCD∽△FAC,
∴,
∴FC2=FD FA,
设FD=3x,则FC=4x,
又∵FC2=FD FA,
即(4x)2=3x(3x+2),
解得x=(取正值),
∴FD=6x=.
21.(1)∠BCD=∠DBC=45°; (2)∠BCD=30°,∠DBC=60°
(1)
解:∵AB是⊙O的直径,BD为⊙O的切线,切点为B,
∴DB⊥AB,
∴∠DBA=90°,
∵DC为⊙O的切线,切点为C,
∴DC=DB,
∵CD∥AB,
∴∠D+∠DBA=180°,
∴∠D=90°,
∴∠BCD=∠DBC=45°;
(2)
解:∵AB是⊙O的直径,DB为⊙O的切线,切点为B,
∴DB⊥AB,
∴∠DBA=90°,
∠DEB=∠EBA,
∴∠BDC=90°,
∵∠EBD=30°,
∴∠DEB=60°,
∴∠EBA=60°,
∴∠ACE=120°,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCD=30°,
∴∠DBC=60°.
答案第1页,共2页
一、单选题
1.如图,分别切于两点,切于点E,交于点.若的周长等于,则线段的长是( )
A. B.3 C. D.
2.如图,PA、PB是的切线,A、B为切点,连接OB、AB,若,则的度数为( )
A.50° B.55° C.65° D.70°
3.如图,从⊙O外一点P引圆的两条切线PA,PB,切点分别是A,B,若∠APB=60°,PA=5,则弦AB的长是( )
A. B. C.5 D.5
4.如图,与的两边分别相切,其中OA边与⊙C相切于点P.若,,则OC的长为( )
A.8 B. C. D.
5.如图所示,已知⊙I是△ABC的内切圆,点I是内心,若∠A=35°,则∠BIC等于( )
A.35° B.70° C.145° D.107.5°
6.如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A.8 B.10 C.12 D.14
7.如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
A. B. C.π 或 D.或
8.如图,PA与⊙O相切于点A,线段PO交⊙O于点C,过点C作⊙O的切线交PA于点B.若PC=4,AB=3,则⊙O的半径等于( )
A.4 B.5 C.6 D.12
9.如图,PA、PB、MN是⊙O的切线,A、B、C是切点,MN分别交线段PA、PB于M、N两点.若∠APB=50°,则∠MON=( )
A.50° B.60° C.65° D.70°
10.如图,锐角△ABC内接于⊙O,I为△ABC内心,已知∠OAB=50°,则∠AIB的度数为( )
A.110° B.125° C.130° D.135°
11.如图,在矩形ABCD中,,,点E、F分别是AD、BC的中点,点P在线段EF上,内切圆半径的最大值是( )
A.1 B. C. D.
12.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=31°,则∠BEC的大小为( )
A.120° B.121° C.122° D.125°
二、填空题
13.已知等腰三角形三边长分别是13、13、10,则这个等腰三角形内切圆半径为____
14.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,若AB=10,AC=7,则BD的长为 ___.
15.如图,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在弧AB上,若PA长为8,则△PEF的周长是_____.
16.已知正方形边长为2,与以的中点为圆心的圆相切交于点,求三角形的面积 __.
17.如图,已知正方形ABCD的边长为4,点E在BC上,DE为以AB为直径的半圆的切线,切点为F,连结CF,则ED的长为______,CF的长为______.
三、解答题
18.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出AB=8cm,这张光盘的直径是多少?(精确到1cm,)
19.如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,若AB=5,AC=6,BC=7,求AD、BE、CF的长.
20.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且CF是⊙O的切线.
(1)求证:∠DCF=∠CAD.
(2)探究线段CF,FD,FA的数量关系并说明理由;
(3)若cosB=,AD=2,求FD的长.
21.已知AB是⊙O的直径,BD为⊙O的切线,切点为B.过⊙O上的点C作,交BD点D.连接AC,BC.
图1 图2
(1)如图①,若DC为⊙O的切线,切点为C.求∠BCD和∠DBC的大小;
(2)如图②,当CD与⊙O交于点E时,连接BE.若∠EBD=30°,求∠BCD和∠DBC的大小.
试卷第1页,共3页
参考答案:
1.A
解:,切于、两点,切于点,交,于,,
,,,
的周长等于,
,
,
故选:A.
2.A
解:∵PA、PB是⊙O的切线,
∴PA=PB,∠OBP=90°,
又∵∠ABO=25°,
∴∠PBA=90°-25°=65°=∠PAB,
∴∠P=180°-65°-65°=50°,
故选:A.
3.C
解:∵PA,PB为⊙O的切线,
∴PA=PB,
∵∠APB=60°,
∴△APB为等边三角形,
∴AB=PA=5.
故选:C.
4.C
解:如图所示,连接CP,
∵OA,OB都是圆C的切线,∠AOB=90°,P为切点,
∴∠CPO=90°,∠COP=45°,
∴∠PCO=∠COP=45°,
∴CP=OP=4,
∴,
故选C.
5.D
解:∵∠A=35°,
∴
∵点I是的内心,
∴
即
∠BIC 107.5°
故选D
6.B
解: ∵∠C=90°,AC=12,BC=5,
∴AB===13,
∵⊙O与Rt△ABC的三边相切于点D、E、F,
,
设,则,
即
解得
故选:B.
7.D
解:如图1,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,
连接WE,WF,CW,OC,OW,则四边形OCFW是矩形,
∴OW=CF,WF=1,
∵∠ACB=60○,
∴∠WCF=∠ACB=30°,
所以点O移动的距离为OW=CF===.
如图2,当圆O滚动到圆O′位置与CA,CB相切,切点分别为F,E,
连接OO′,O′E,O′C,O′F,OC,则四边形OCEO′是矩形,
∴OO′=CE,
∵∠ACB=60○,
∴∠ACE=120○,
∴∠O′CE=60°,
∴点O移动的距离为OO′=CE===,·
故选:D.
8.C
解:设⊙O的半径为r,
由切线长定理得,BC=BA=3,
∵BC是⊙O的切线,
∴∠BCP=90°,
∴PB==5,
∴AP=PB+AB=8,
∵PA是⊙O的切线,
∴∠OAP=90°,
∴AP2+OA2=OP2,即82+r2=(4+r)2,
解得,r=6,
故选:C.
9.C
解:连接AO,BO,OC,
∵PA、PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∵∠APB=50°,
∴∠AOB=360°-2×90°-50°=130°,
∵PA、PB、MN是⊙O的切线,
∴∠BNO=∠CNO,∠AMO=∠CMO,
∴∠BON=∠CON,AOM=∠COM,
∴∠MON=∠CON+∠COM=∠AOB=65°.
故选:C.
10.A
解:连接OB,
∵OA=OB,
∴∠OAB=∠OBA=50°,
∴∠O=180°﹣(∠OAB+∠OBA)=80°,
∴∠C=40°,
∵I为△ABC内心,
∴AI、BI为∠CAB、∠CBA的平分线,
∴,,
∴,
∴∠AIB=180°﹣(∠IAB+∠IBA)=180°﹣70°=110°.
故选:A.
11.D
解:∵点E、F分别是AD、BC的中点,四边形ABCD是矩形,
∴EF∥AB,
∵P在EF上,AB=8,BC=6,
∴S△PAB=×8×3=12,
设△PAB内切圆半径是r,
∵S△PAB=(AP+PB+AB) r=12,
∴AP+BP最小时,r有最大值,
如图,F是BC的中点,所以点B关于EF的对称点是C点,连接CA与EF交于点P',
∵AP+BP=AP+CP≥CA,
∴此时CA即为AP+BP最小值,
∵AB=8,AD=6,
∴AC==10,
∴AP+BP最小值为10,
∴PA=PB=5,
∴×5×r+×5×r+×8×r=12,
解得r=,
故选:D.
12.B
解:在⊙O中,∠CBD=31°,
∴∠CAD=31°,
∵点E是△ABC的内心,
∴∠BAC=2∠CAD=62°,
∴∠EBC+∠ECB=(180°-62°)÷2=59°,
∴∠BEC=180°-59°=121°.
故选:B.
13.
解:等腰△ABC中,AB=AC,AD为BC边上的高,故AD为BC边上的中线,即BD=DC,
在直角△ABD中,AB=13,BD=5,
∴AD==12,
则S△ABC=×10×12=60.
∵S△ABC=(13+13+10)r,
∴内切圆的半径r=,
故答案为:.
14.
解:∵AC与⊙O相切于点C、AB与⊙O相切于点P,
∴AC=AP=7,
∵AB=10,
∴BP=AB-AP=10-7=3,
∵BD与⊙O相切于点D、BP与⊙O相切于点P,
∴BD=BP=3,
∴BD的长为3,
故答案为:3.
15.16
解:∵PA、PB、EF分别与⊙O相切于点A、B、C,
∴AE=CE,FB=CF,PA=PB=8,
∴△PEF的周长=PE+EF+PF=PA+PB=16.
故答案为:16.
16.
解:设与圆相切于点,
四边形是正方形,
,,
、是圆的半径,
与圆相切于点,与圆相切于点,
,,
设,
则,,
∵在中,,
,
解得:,
,
三角形的面积,
故答案为:1.5.
17. 5 ##
解:∵正方形ABCD
∴CD=AD=BC=4,CE⊥AB,DA⊥AB
∵以AB为直径的半圆
∴BE、AD也是半圆的切线
∵DE为以AB为直径的半圆的切线,
∴EB=EF、DA=DF=4
∴EC=BC-BE=4-EF,DE=DF+EF=4+EF
在Rt△DCE中,
∴
解得
∴DE=DF+EF=4+EF=5
过F作FG⊥DC于G,如图
∴
∴
∴
解得
∴
∴在Rt△CFG中,
故答案为:5,
18.28 cm
解:设光盘的圆心为O,连接OC,OB,OA,如图所示:
∵AC,AB分别为圆O的切线,
∴OC⊥AC,OB⊥AB,
∵OC,OB都是圆O的半径
∴OC=OB
∴AO为∠CAB的平分线,
∵∠CAD=60°,∠CAD+∠CAB=180°
∴∠CAB=180°-∠CAD=120°
∴∠OAC=∠OAB=∠CAB=60°,
在Rt△AOB中,∠OBA=90°,∠OAB=60°,AB=8cm,
∴tan∠OAB=tan60°=,即=,
∴OB=8cm,
则光盘的直径为16≈28 cm.
故答案为:28 cm
19.AD=2,BE=3,CF=4
解:∵⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F,
∴AD=AF,BD=BE,CE=CF,
可设AD=AF=x,BD=BE=y,CE=CF=z,
∵AB=5,AC=6,BC=7,
∴AD+BD=5,AF+CF=6,BE+CE=7,
∴x+y=5①,x+z=6②,y+z=7③,
由①+②+③,得:x+y+z=9④,
由④-①,得:z=4,
把z=4分别代入②,③得:x=2,y=3,
即AD=2,BE=3,CF=4.
20.(1)证明过程见详解 (2)FC2=FD FA;理由见详解 (3)
(1)
证明:如图,连接OC,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠OCD+∠OCA=90°,
∵FC是⊙O的切线,
∴∠DCF+∠OCD=90°,
∴∠OCA=∠DCF,
∵OC=OA,
∴∠CAD=∠OCA,
∴∠DCF=∠CAD;
(2)
解:FC2=FD FA,理由如下:
∵∠FCD=∠FAC,∠F=∠F,
∴△FCD∽△FAC,
∴,
∴FC2=FD FA;
(3)
解:∵∠B=∠ADC,cosB=,
∴cos∠ADC=,
在Rt△ACD中,
∵cos∠ADC==,
∴,
由(2)知△FCD∽△FAC,
∴,
∴FC2=FD FA,
设FD=3x,则FC=4x,
又∵FC2=FD FA,
即(4x)2=3x(3x+2),
解得x=(取正值),
∴FD=6x=.
21.(1)∠BCD=∠DBC=45°; (2)∠BCD=30°,∠DBC=60°
(1)
解:∵AB是⊙O的直径,BD为⊙O的切线,切点为B,
∴DB⊥AB,
∴∠DBA=90°,
∵DC为⊙O的切线,切点为C,
∴DC=DB,
∵CD∥AB,
∴∠D+∠DBA=180°,
∴∠D=90°,
∴∠BCD=∠DBC=45°;
(2)
解:∵AB是⊙O的直径,DB为⊙O的切线,切点为B,
∴DB⊥AB,
∴∠DBA=90°,
∠DEB=∠EBA,
∴∠BDC=90°,
∵∠EBD=30°,
∴∠DEB=60°,
∴∠EBA=60°,
∴∠ACE=120°,
∵AB是⊙O的直径,
∴∠BCA=90°,
∴∠BCD=30°,
∴∠DBC=60°.
答案第1页,共2页
