2021-2022学年人教版七年级数学下册8.3实际问题与二元一次方程组(销售利润问题、几何问题)课后练习(word版含简单答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册8.3实际问题与二元一次方程组(销售利润问题、几何问题)课后练习(word版含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 108.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 10:23:53 | ||
图片预览


文档简介
2021-2022学年人教版七年级数学下册 第八章 二元一次方程组
8.3 实际问题与二元一次方程组(销售利润问题、几何问题) 课后练习
一、选择题
1.为迎接2022年北京冬奧会,某班开展了以迎冬奥为主题的体育活动,计划拿出200元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件25元,乙种奖品每件10元,则购买方案有( )
A.2种 B.3种 C.4种 D.5种
2.某超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入144元;第2天,卖出18支牙刷和11盒牙膏,收入219元;第3天,卖出23支牙刷和20盒牙膏,收入368元;第4天,卖出17支牙刷和11盒牙膏,收入216元,聪明的小方发现这四天中有一天的记录有误,其中记录有误的是( )
A.第1天 B.第2天 C.第3天 D.第4天
3.某商场新购进一种服装,每套售价1000元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价比原来提高了2%,则调价前上衣的单价是( )
A.200元 B.480元 C.600元 D.800元
4.麦当劳甜品站进行促销活动,同一种甜品第一件正价,第二件半价,现购买同一种甜品2件,相当于这两件甜品售价与原价相比共打了( )
A.5折 B.5.5折 C.7折 D.7.5折
5.某商店对一种商品进行促销,促销方式:若购买不超过10件,按每件元付款:若一次性购买10件以上,超出部分按每件元付款.小明购买了14件付款90元;小聪购买了19件付款115元,则,的值为( )
A. B. C. D.
6.将8个一样大小的长方形,恰好可以拼成一个大的长方形如图1,将这8个一样大小的长方形拼成了如图2那样的正方形,中间还留了一个洞,恰好是边长为3m的小正方形,则一个小长方形的面积为( )
A.120m2 B.135m2 C.108m2 D.96m2
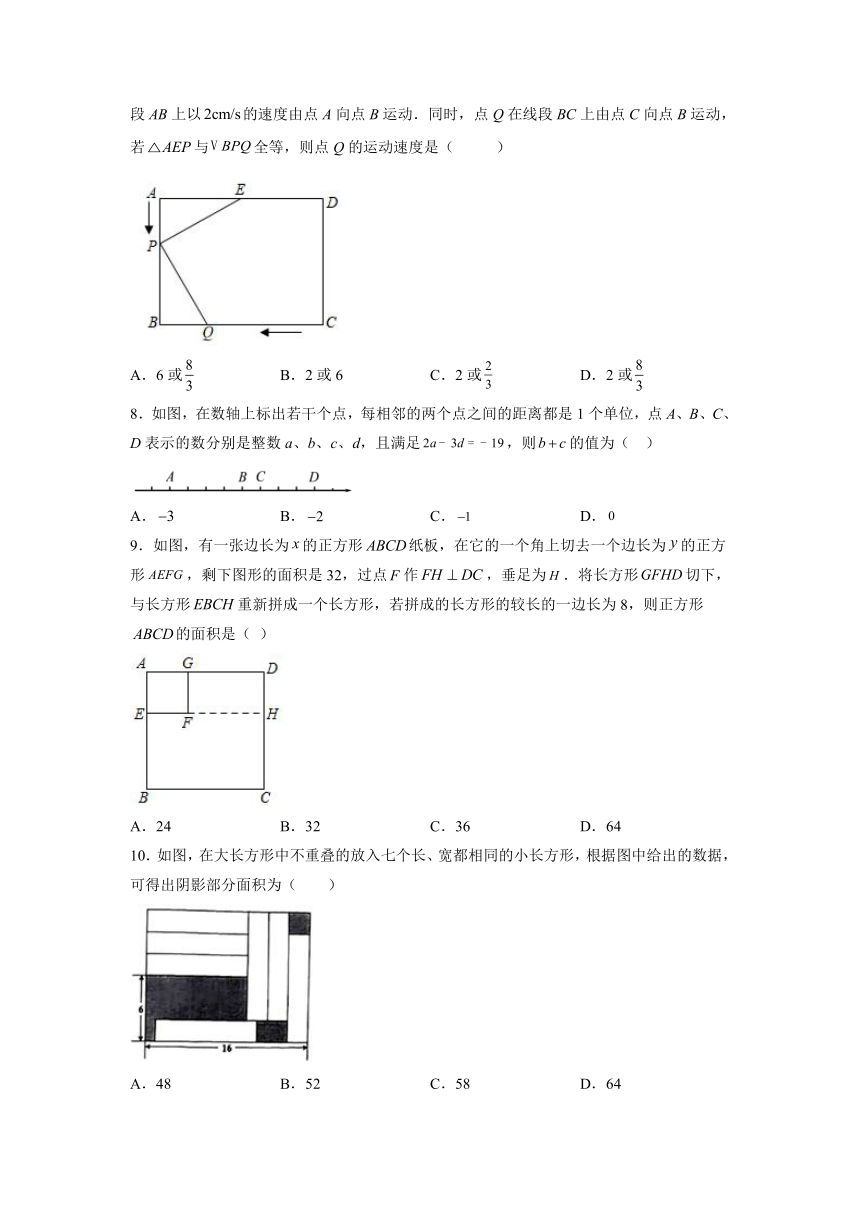
7.如图,已知长方形中,,,点E为AD的中点,若点P在线段AB上以的速度由点A向点B运动.同时,点Q在线段BC上由点C向点B运动,若与全等,则点Q的运动速度是( )
A.6或 B.2或6 C.2或 D.2或
8.如图,在数轴上标出若干个点,每相邻的两个点之间的距离都是1个单位,点A、B、C、D表示的数分别是整数a、b、c、d,且满足,则的值为( )
A. B. C. D.
9.如图,有一张边长为的正方形纸板,在它的一个角上切去一个边长为的正方形,剩下图形的面积是32,过点作,垂足为.将长方形切下,与长方形重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形的面积是( )
A.24 B.32 C.36 D.64
10.如图,在大长方形中不重叠的放入七个长、宽都相同的小长方形,根据图中给出的数据,可得出阴影部分面积为( )
A.48 B.52 C.58 D.64
二、填空题
11.春节临近,各种新鲜水果大量上市.某商人根据市场调查,购进糖心苹果和车厘子两种水果,已知销售每斤糖心苹果的利润率为30%,每斤车厘子的利润率为50%.当售出的糖心苹果和车厘子的数量之比为4:3时,商人得到的总利润率为40%.要使商人得到的总利润率为46%,那么售出的糖心苹果和车厘子的数量之比为____.
12.端午节是中国传统节日,人们有吃粽子的习俗.某商场从6月12日起开始打折促销,肉粽六折,白粽七折,打折前购买4盒肉粽和5盒白粽需350元,打折后购买5盒肉粽和10盒白粽需360元.轩轩同学想在今天中考结束后,为敬老院送肉粽和白粽各5盒,则他6月13日购买的花费比在打折前购买节省_____元.
13.打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花__元.
14.若与互为补角,并且的一半比小,则的度数为_________.
15.如图所示,矩形ABCD被分成一些正方形,已知AB=32cm,则矩形的另一边AD=________cm.
三、解答题
16.某公司组织“爱心义卖”活动,购进了黑白两种颜色的文化衫共100件,进行手绘设计后出售,所获利润全部捐给山区困难儿童.每件文化衫的批发价和零售价如表:
批发价(元) 零售价(元)
黑色文化衫 10 25
白色文化衫 8 20
假设文化衫全部售出,共获利1380元,求购进黑白两种文化衫各多少件?
17.某超市计划购买甲、乙两种玩具,已知购买2件甲种玩具与1件乙种玩具共需87元,购买1件甲种玩具与2件乙种玩具共需84元.
(1)求甲、乙两种玩具每件的价格分别是多少元;
(2)如果卖方仅给予甲种玩具优惠,优惠方案为:购进甲种玩具超过a件时,超出部分可以享受7折优惠.若购买30件甲种玩具需支付855元,求a的值.
18.某商店销售10台A型和20台B型计算器的利润为400元,销售15台A型和10台B型计算器的利润为300元.
(1)求每台A型计算器和B型计算器的销售利润;
(2)该商店计划一次购进两种型号的计算器共50台,设购进A型计算器a台,这50台计算器的销售总利润为w元.求w关于a的函数关系式.
19.某天,信美超市用360元钱按批发价从水果批发市场购买了苹果和香蕉共200kg,然后按零售价出售,苹果和香蕉当天的批发价和零售价如下表所示:
品名 苹果 香蕉
批发价(单位:元/kg) 2.0 1.5
零售价(单位:元/kg) 2.4 1.8
(1)这一天该超市购买苹果和香蕉各多少kg?
(2)如果苹果和香蕉全部以零售价售出,该超市当天卖这些苹果和香蕉共赚了多少钱?
20.数学活动课上,小新和小葵各自拿着不同的长方形纸片在做数学问题探究.
(1)小新经过测量和计算得到长方形纸片的长宽之比为3:2,面积为30,请求出该长方形纸片的长和宽;
(2)小葵在长方形内画出边长为a,b的两个正方形(如图所示),其中小正方形的一条边在大正方形的一条边上,她经过测量和计算得到长方形纸片的周长为50,阴影部分两个长方形的周长之和为30,由此她判断大正方形的面积为100,间小葵的判断正确吗?请说明理由.
21.小美手中有块长方形的硬纸片,其中长BC比宽AB多10cm,长方形的周长是100cm.
(1)求长方形的面积.
(2)现小美想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为4:3,面积为588cm2的新长方形纸片.试判断小美能否成功,请说明理由.
22.萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)写出用含x、y的整式表示地面总面积;
(2)已知客厅面积是厨房面积的4倍,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
23.聪聪与明明分别要把两块边长都为的正方形薄钢片要制作成两个无盖的长方体盒子(不计粘合部分).
(1)聪聪先在薄钢片四个角截去边长为的四个相同的小正方形(如图①),然后把四边折合粘在一起,便得到甲种盒子,请你帮忙求出该种盒子底面边长;
(2)明明截去两角后(如图②),沿虚线折合粘在一起,便得到乙种盒子(如图③),已知乙种盒子底面的长是宽的2倍,求乙种盒子底面的长与宽分别是多少?
(3)若把乙种盒子装满水后,倒入甲种盒子内,问是否可以装满甲种盒子,若能装满甲种盒子,那么乙种盒子里的水面有多高?若不能装满甲种盒子,求出此甲种盒子的水面的高度.
【参考答案】
1.B 2.C 3.D 4.D 5.A 6.B 7.A 8.C 9.C 10.B
11.1:3
12.145
13.400
14.
15.29
16.购进黑色文化衫60件,白色文化衫40件
17.(1)甲种玩具玩具每件的价格为30元,乙种玩具每件的价格为27元
(2)25
18.(1)每台A型计算器的销售利润10元,每台B型计算器的销售利润15元
(2)
19.(1)苹果120kg,香蕉80kg;(2)72元
20.(1)长为,宽为;(2)正确,理由见解析
21.(1)长方形的面积为600cm2;(2)不能成功,理由详见解析.
22.(1);(2)3600元
23.(1)甲种盒子底面长;(2)乙种盒子长为,宽为;(3)不能,甲种盒子里的水面高
8.3 实际问题与二元一次方程组(销售利润问题、几何问题) 课后练习
一、选择题
1.为迎接2022年北京冬奧会,某班开展了以迎冬奥为主题的体育活动,计划拿出200元钱全部用于购买甲、乙两种奖品(两种奖品都购买),奖励表现突出的学生,已知甲种奖品每件25元,乙种奖品每件10元,则购买方案有( )
A.2种 B.3种 C.4种 D.5种
2.某超市以同样的价格卖出同样的牙刷和牙膏,以下是4天的记录:第1天,卖出13支牙刷和7盒牙膏,收入144元;第2天,卖出18支牙刷和11盒牙膏,收入219元;第3天,卖出23支牙刷和20盒牙膏,收入368元;第4天,卖出17支牙刷和11盒牙膏,收入216元,聪明的小方发现这四天中有一天的记录有误,其中记录有误的是( )
A.第1天 B.第2天 C.第3天 D.第4天
3.某商场新购进一种服装,每套售价1000元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价比原来提高了2%,则调价前上衣的单价是( )
A.200元 B.480元 C.600元 D.800元
4.麦当劳甜品站进行促销活动,同一种甜品第一件正价,第二件半价,现购买同一种甜品2件,相当于这两件甜品售价与原价相比共打了( )
A.5折 B.5.5折 C.7折 D.7.5折
5.某商店对一种商品进行促销,促销方式:若购买不超过10件,按每件元付款:若一次性购买10件以上,超出部分按每件元付款.小明购买了14件付款90元;小聪购买了19件付款115元,则,的值为( )
A. B. C. D.
6.将8个一样大小的长方形,恰好可以拼成一个大的长方形如图1,将这8个一样大小的长方形拼成了如图2那样的正方形,中间还留了一个洞,恰好是边长为3m的小正方形,则一个小长方形的面积为( )
A.120m2 B.135m2 C.108m2 D.96m2
7.如图,已知长方形中,,,点E为AD的中点,若点P在线段AB上以的速度由点A向点B运动.同时,点Q在线段BC上由点C向点B运动,若与全等,则点Q的运动速度是( )
A.6或 B.2或6 C.2或 D.2或
8.如图,在数轴上标出若干个点,每相邻的两个点之间的距离都是1个单位,点A、B、C、D表示的数分别是整数a、b、c、d,且满足,则的值为( )
A. B. C. D.
9.如图,有一张边长为的正方形纸板,在它的一个角上切去一个边长为的正方形,剩下图形的面积是32,过点作,垂足为.将长方形切下,与长方形重新拼成一个长方形,若拼成的长方形的较长的一边长为8,则正方形的面积是( )
A.24 B.32 C.36 D.64
10.如图,在大长方形中不重叠的放入七个长、宽都相同的小长方形,根据图中给出的数据,可得出阴影部分面积为( )
A.48 B.52 C.58 D.64
二、填空题
11.春节临近,各种新鲜水果大量上市.某商人根据市场调查,购进糖心苹果和车厘子两种水果,已知销售每斤糖心苹果的利润率为30%,每斤车厘子的利润率为50%.当售出的糖心苹果和车厘子的数量之比为4:3时,商人得到的总利润率为40%.要使商人得到的总利润率为46%,那么售出的糖心苹果和车厘子的数量之比为____.
12.端午节是中国传统节日,人们有吃粽子的习俗.某商场从6月12日起开始打折促销,肉粽六折,白粽七折,打折前购买4盒肉粽和5盒白粽需350元,打折后购买5盒肉粽和10盒白粽需360元.轩轩同学想在今天中考结束后,为敬老院送肉粽和白粽各5盒,则他6月13日购买的花费比在打折前购买节省_____元.
13.打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花__元.
14.若与互为补角,并且的一半比小,则的度数为_________.
15.如图所示,矩形ABCD被分成一些正方形,已知AB=32cm,则矩形的另一边AD=________cm.
三、解答题
16.某公司组织“爱心义卖”活动,购进了黑白两种颜色的文化衫共100件,进行手绘设计后出售,所获利润全部捐给山区困难儿童.每件文化衫的批发价和零售价如表:
批发价(元) 零售价(元)
黑色文化衫 10 25
白色文化衫 8 20
假设文化衫全部售出,共获利1380元,求购进黑白两种文化衫各多少件?
17.某超市计划购买甲、乙两种玩具,已知购买2件甲种玩具与1件乙种玩具共需87元,购买1件甲种玩具与2件乙种玩具共需84元.
(1)求甲、乙两种玩具每件的价格分别是多少元;
(2)如果卖方仅给予甲种玩具优惠,优惠方案为:购进甲种玩具超过a件时,超出部分可以享受7折优惠.若购买30件甲种玩具需支付855元,求a的值.
18.某商店销售10台A型和20台B型计算器的利润为400元,销售15台A型和10台B型计算器的利润为300元.
(1)求每台A型计算器和B型计算器的销售利润;
(2)该商店计划一次购进两种型号的计算器共50台,设购进A型计算器a台,这50台计算器的销售总利润为w元.求w关于a的函数关系式.
19.某天,信美超市用360元钱按批发价从水果批发市场购买了苹果和香蕉共200kg,然后按零售价出售,苹果和香蕉当天的批发价和零售价如下表所示:
品名 苹果 香蕉
批发价(单位:元/kg) 2.0 1.5
零售价(单位:元/kg) 2.4 1.8
(1)这一天该超市购买苹果和香蕉各多少kg?
(2)如果苹果和香蕉全部以零售价售出,该超市当天卖这些苹果和香蕉共赚了多少钱?
20.数学活动课上,小新和小葵各自拿着不同的长方形纸片在做数学问题探究.
(1)小新经过测量和计算得到长方形纸片的长宽之比为3:2,面积为30,请求出该长方形纸片的长和宽;
(2)小葵在长方形内画出边长为a,b的两个正方形(如图所示),其中小正方形的一条边在大正方形的一条边上,她经过测量和计算得到长方形纸片的周长为50,阴影部分两个长方形的周长之和为30,由此她判断大正方形的面积为100,间小葵的判断正确吗?请说明理由.
21.小美手中有块长方形的硬纸片,其中长BC比宽AB多10cm,长方形的周长是100cm.
(1)求长方形的面积.
(2)现小美想用这块长方形的硬纸片,沿着边的方向裁出一块长与宽的比为4:3,面积为588cm2的新长方形纸片.试判断小美能否成功,请说明理由.
22.萱萱家为方便她上学,在黄冈小河中学旁边购买了一套经济适用房.她家准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
(1)写出用含x、y的整式表示地面总面积;
(2)已知客厅面积是厨房面积的4倍,且地面总面积是卫生间面积的15倍,铺1m2地砖的平均费用为80元,求铺地砖的总费用为多少元?
23.聪聪与明明分别要把两块边长都为的正方形薄钢片要制作成两个无盖的长方体盒子(不计粘合部分).
(1)聪聪先在薄钢片四个角截去边长为的四个相同的小正方形(如图①),然后把四边折合粘在一起,便得到甲种盒子,请你帮忙求出该种盒子底面边长;
(2)明明截去两角后(如图②),沿虚线折合粘在一起,便得到乙种盒子(如图③),已知乙种盒子底面的长是宽的2倍,求乙种盒子底面的长与宽分别是多少?
(3)若把乙种盒子装满水后,倒入甲种盒子内,问是否可以装满甲种盒子,若能装满甲种盒子,那么乙种盒子里的水面有多高?若不能装满甲种盒子,求出此甲种盒子的水面的高度.
【参考答案】
1.B 2.C 3.D 4.D 5.A 6.B 7.A 8.C 9.C 10.B
11.1:3
12.145
13.400
14.
15.29
16.购进黑色文化衫60件,白色文化衫40件
17.(1)甲种玩具玩具每件的价格为30元,乙种玩具每件的价格为27元
(2)25
18.(1)每台A型计算器的销售利润10元,每台B型计算器的销售利润15元
(2)
19.(1)苹果120kg,香蕉80kg;(2)72元
20.(1)长为,宽为;(2)正确,理由见解析
21.(1)长方形的面积为600cm2;(2)不能成功,理由详见解析.
22.(1);(2)3600元
23.(1)甲种盒子底面长;(2)乙种盒子长为,宽为;(3)不能,甲种盒子里的水面高
