2021-2022学年苏科版八年级数学下册第9章中心对称图形—平行四边形培优试题(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册第9章中心对称图形—平行四边形培优试题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 143.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 10:32:15 | ||
图片预览


文档简介
第9章《中心对称图形—平行四边形》培优试题2021-2022学年苏科版八年级数学下册
一.选择题(共10小题,每小题3分,共30分)
1.如图,将△ABC绕点A逆时针方向旋转110°,得到△AB'C',若点B'在线段BC的延长线上,则∠BB'C'的度数为( )
A.65° B.70° C.75° D.80°
2.下列既是轴对称图形又是中心对称图形的是( )
A.菱形 B.平行四边形 C.等边三角形 D.等腰梯形
3.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45° B.每一个内角都小于45°
C.有一个内角大于等于45° D.每一个内角都大于等于45°
4.如图,在 ABCD中,AD=8,AB=5,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,则EF=( )
A.2 B.2.5 C.3 D.3.5
5.菱形ABCD的边长为8,有一个内角为120°,则较长的对角线的长为( )
A. B.8 C. D.4
6.下列关于菱形的说法中不正确的是( )
A.菱形的四条边相等 B.菱形的面积等于对角线乘积的一半
C.菱形的对角线相等且互相垂直 D.对角线互相垂直且平分的四边形是菱形
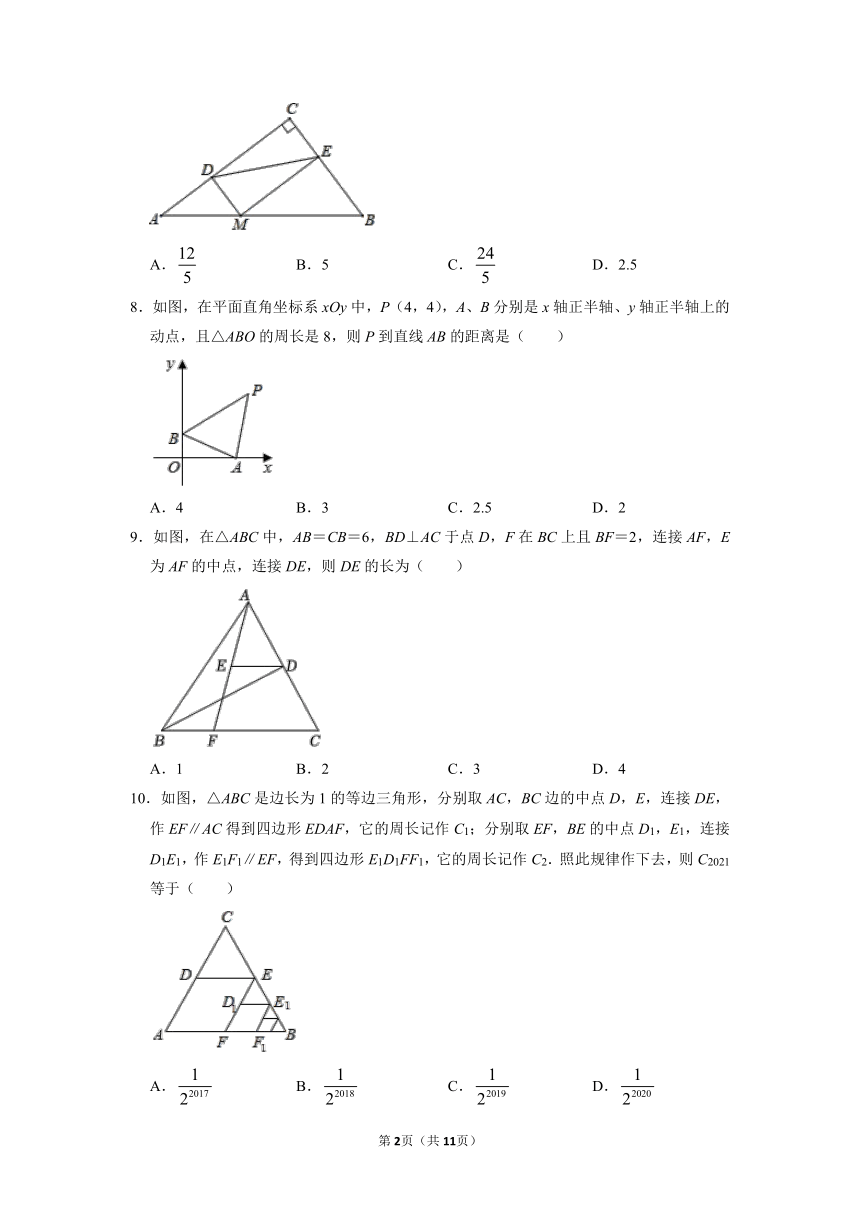
7.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
8.如图,在平面直角坐标系xOy中,P(4,4),A、B分别是x轴正半轴、y轴正半轴上的动点,且△ABO的周长是8,则P到直线AB的距离是( )
A.4 B.3 C.2.5 D.2
9.如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
10.如图,△ABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作EF∥AC得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1,E1,连接D1E1,作E1F1∥EF,得到四边形E1D1FF1,它的周长记作C2.照此规律作下去,则C2021等于( )
A. B. C. D.
二.填空题(共8小题,每小题4分,共32分)
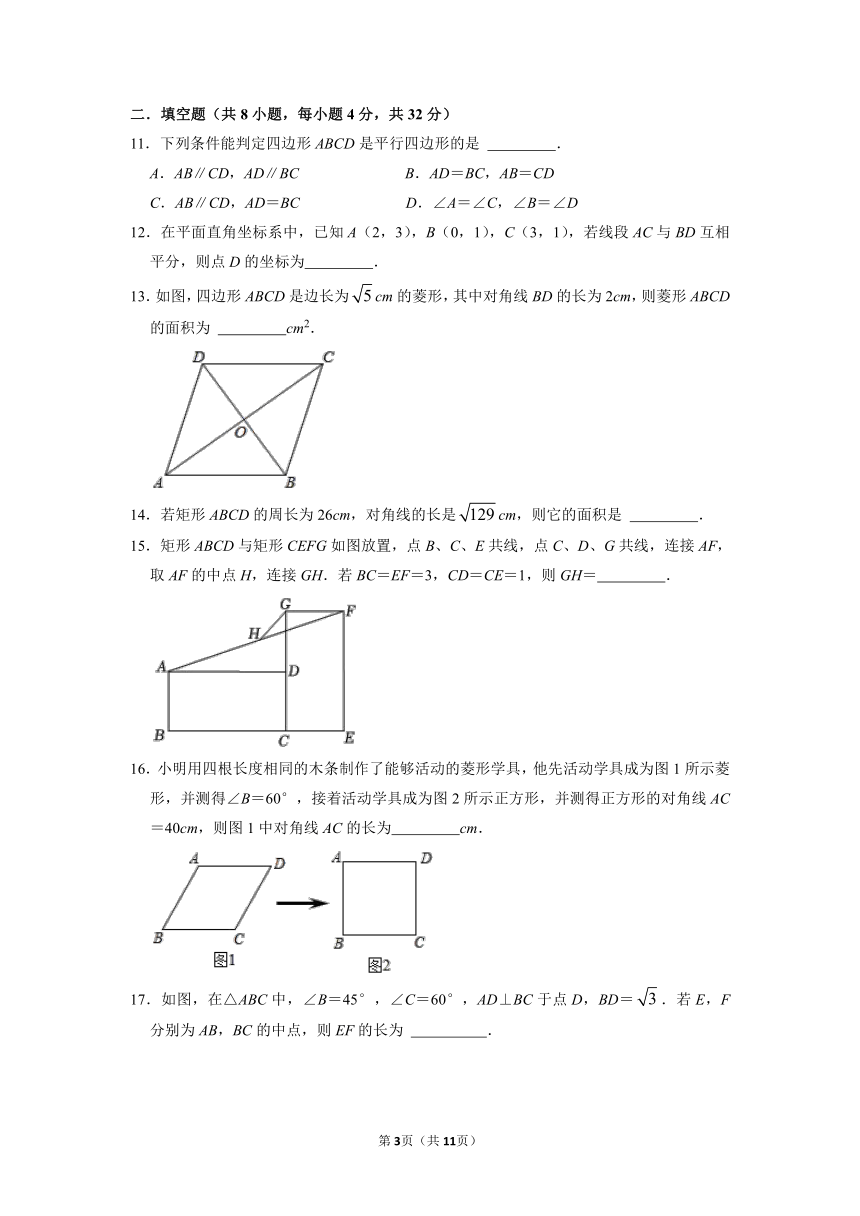
11.下列条件能判定四边形ABCD是平行四边形的是 .
A.AB∥CD,AD∥BC B.AD=BC,AB=CD
C.AB∥CD,AD=BC D.∠A=∠C,∠B=∠D
12.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D的坐标为 .
13.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
14.若矩形ABCD的周长为26cm,对角线的长是cm,则它的面积是 .
15.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH= .
16.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得正方形的对角线AC=40cm,则图1中对角线AC的长为 cm.
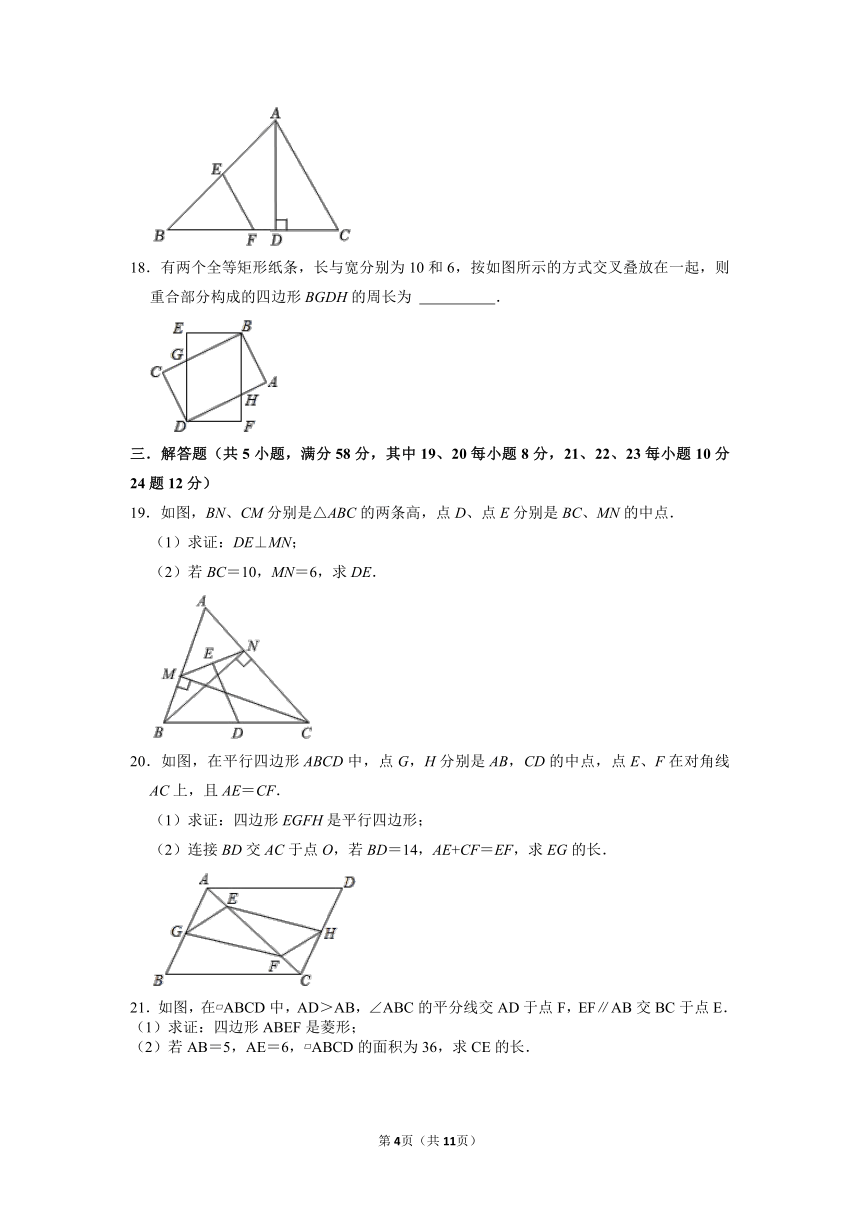
17.如图,在△ABC中,∠B=45°,∠C=60°,AD⊥BC于点D,BD=.若E,F分别为AB,BC的中点,则EF的长为 .
18.有两个全等矩形纸条,长与宽分别为10和6,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为 .
三.解答题(共5小题,满分58分,其中19、20每小题8分,21、22、23每小题10分24题12分)
19.如图,BN、CM分别是△ABC的两条高,点D、点E分别是BC、MN的中点.
(1)求证:DE⊥MN;
(2)若BC=10,MN=6,求DE.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
21.如图,在 ABCD中,AD>AB,∠ABC的平分线交AD于点F,EF∥AB交BC于点E.
(1)求证:四边形ABEF是菱形;
(2)若AB=5,AE=6, ABCD的面积为36,求CE的长.
22.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=5,AE=3,求菱形ABCD的面积.
23.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 .
第9章《中心对称图形—平行四边形》培优试题2021-2022学年苏科版八年级数学下册参考简答
一.选择题(共10小题)
1.B. 2.A. 3.D. 4.A. 5.A. 6.C. 7.A. 8.A.
9.B. 10.C.
二.填空题(共8小题)
11. ABD . 12. (5,3) . 13. 4 . 14. 20cm .
15. . 16. 20 cm. 17. 1 . 18. .
三.解答题(共5小题)
19.如图,BN、CM分别是△ABC的两条高,点D、点E分别是BC、MN的中点.
(1)求证:DE⊥MN;
(2)若BC=10,MN=6,求DE.
【解】:(1)证明:如图,连接DM,DN.
∵BN、CM分别是△ABC的两条高,
∴BN⊥AC,CM⊥AB,
∴∠BMC=∠CNB=90°,
∵D是BC的中点,
∴DM=BC,DN=BC,
∴DM=DN,
∵E为MN的中点,
∴DE⊥MN;
(2)解:∵BC=10,
∴DM=5,
∵点E是MN的中点,MN=6,
∴ME=4,
由勾股定理得:DE==4.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
【解】:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
, ∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=.
21.如图,在 ABCD中,AD>AB,∠ABC的平分线交AD于点F,EF∥AB交BC于点E.
(1)求证:四边形ABEF是菱形;
(2)若AB=5,AE=6, ABCD的面积为36,求CE的长.
【解】:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABEF是平行四边形,
∵BF平分∠ABC,
∴∠ABF=∠EBF,
∵AF∥BC,
∴∠AFB=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
∴四边形ABEF是菱形;
(2)∵四边形ABEF是菱形,
∴AE⊥BF,AO=OE=3,BO=OF,AB=BE=5,
∴BO===4,
∴BF=8,
∴菱形ABEF的面积=×6×8=24,
∵AD∥BC,AB∥EF∥CD,
∴四边形ECDF是平行四边形,
∴ S EFDC=36﹣24=12,
∴ S菱形ABFE:S EFDC=2:1,
∴BE:EC=2:1,
∴EC=.
22.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=5,AE=3,求菱形ABCD的面积.
【解】:(1)四边形AEBO是矩形,理由如下:
∵BE∥AC,AE∥BD
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O
∴AC⊥BD,即∠AOB=90°.
∴四边形AEBO是矩形;
(2)∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵四边形AEBO是矩形,
∴AB=OE=5,
∴OB=AE=3,
∴AO===4,
∴BD=2OB=6,AC=2AO=8,
∴菱形ABCD的面积=AC×BD=×8×6=24.
23.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 2 .
【解】:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
, ∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)①CE⊥CG,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
, ∴△ADE≌△CDG(SAS),
∴∠CDA=∠DCG,
∵∠ACD+∠CAD+∠ADC=180°,∠ADC=90°,
∴∠ACG=∠ACD+∠DCG=∠ACD+∠CAD=90°,
∴CE⊥CG;
②由①知,△ADE≌△CDG,
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×=2,
第1页(共11页)
一.选择题(共10小题,每小题3分,共30分)
1.如图,将△ABC绕点A逆时针方向旋转110°,得到△AB'C',若点B'在线段BC的延长线上,则∠BB'C'的度数为( )
A.65° B.70° C.75° D.80°
2.下列既是轴对称图形又是中心对称图形的是( )
A.菱形 B.平行四边形 C.等边三角形 D.等腰梯形
3.用反证法证明命题“钝角三角形中必有一个内角小于45°”时,首先应该假设这个三角形中( )
A.有一个内角小于45° B.每一个内角都小于45°
C.有一个内角大于等于45° D.每一个内角都大于等于45°
4.如图,在 ABCD中,AD=8,AB=5,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,则EF=( )
A.2 B.2.5 C.3 D.3.5
5.菱形ABCD的边长为8,有一个内角为120°,则较长的对角线的长为( )
A. B.8 C. D.4
6.下列关于菱形的说法中不正确的是( )
A.菱形的四条边相等 B.菱形的面积等于对角线乘积的一半
C.菱形的对角线相等且互相垂直 D.对角线互相垂直且平分的四边形是菱形
7.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC于点D,过M作ME⊥CB于点E,则线段DE的最小值为( )
A. B.5 C. D.2.5
8.如图,在平面直角坐标系xOy中,P(4,4),A、B分别是x轴正半轴、y轴正半轴上的动点,且△ABO的周长是8,则P到直线AB的距离是( )
A.4 B.3 C.2.5 D.2
9.如图,在△ABC中,AB=CB=6,BD⊥AC于点D,F在BC上且BF=2,连接AF,E为AF的中点,连接DE,则DE的长为( )
A.1 B.2 C.3 D.4
10.如图,△ABC是边长为1的等边三角形,分别取AC,BC边的中点D,E,连接DE,作EF∥AC得到四边形EDAF,它的周长记作C1;分别取EF,BE的中点D1,E1,连接D1E1,作E1F1∥EF,得到四边形E1D1FF1,它的周长记作C2.照此规律作下去,则C2021等于( )
A. B. C. D.
二.填空题(共8小题,每小题4分,共32分)
11.下列条件能判定四边形ABCD是平行四边形的是 .
A.AB∥CD,AD∥BC B.AD=BC,AB=CD
C.AB∥CD,AD=BC D.∠A=∠C,∠B=∠D
12.在平面直角坐标系中,已知A(2,3),B(0,1),C(3,1),若线段AC与BD互相平分,则点D的坐标为 .
13.如图,四边形ABCD是边长为cm的菱形,其中对角线BD的长为2cm,则菱形ABCD的面积为 cm2.
14.若矩形ABCD的周长为26cm,对角线的长是cm,则它的面积是 .
15.矩形ABCD与矩形CEFG如图放置,点B、C、E共线,点C、D、G共线,连接AF,取AF的中点H,连接GH.若BC=EF=3,CD=CE=1,则GH= .
16.小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,接着活动学具成为图2所示正方形,并测得正方形的对角线AC=40cm,则图1中对角线AC的长为 cm.
17.如图,在△ABC中,∠B=45°,∠C=60°,AD⊥BC于点D,BD=.若E,F分别为AB,BC的中点,则EF的长为 .
18.有两个全等矩形纸条,长与宽分别为10和6,按如图所示的方式交叉叠放在一起,则重合部分构成的四边形BGDH的周长为 .
三.解答题(共5小题,满分58分,其中19、20每小题8分,21、22、23每小题10分24题12分)
19.如图,BN、CM分别是△ABC的两条高,点D、点E分别是BC、MN的中点.
(1)求证:DE⊥MN;
(2)若BC=10,MN=6,求DE.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
21.如图,在 ABCD中,AD>AB,∠ABC的平分线交AD于点F,EF∥AB交BC于点E.
(1)求证:四边形ABEF是菱形;
(2)若AB=5,AE=6, ABCD的面积为36,求CE的长.
22.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=5,AE=3,求菱形ABCD的面积.
23.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 .
第9章《中心对称图形—平行四边形》培优试题2021-2022学年苏科版八年级数学下册参考简答
一.选择题(共10小题)
1.B. 2.A. 3.D. 4.A. 5.A. 6.C. 7.A. 8.A.
9.B. 10.C.
二.填空题(共8小题)
11. ABD . 12. (5,3) . 13. 4 . 14. 20cm .
15. . 16. 20 cm. 17. 1 . 18. .
三.解答题(共5小题)
19.如图,BN、CM分别是△ABC的两条高,点D、点E分别是BC、MN的中点.
(1)求证:DE⊥MN;
(2)若BC=10,MN=6,求DE.
【解】:(1)证明:如图,连接DM,DN.
∵BN、CM分别是△ABC的两条高,
∴BN⊥AC,CM⊥AB,
∴∠BMC=∠CNB=90°,
∵D是BC的中点,
∴DM=BC,DN=BC,
∴DM=DN,
∵E为MN的中点,
∴DE⊥MN;
(2)解:∵BC=10,
∴DM=5,
∵点E是MN的中点,MN=6,
∴ME=4,
由勾股定理得:DE==4.
20.如图,在平行四边形ABCD中,点G,H分别是AB,CD的中点,点E、F在对角线AC上,且AE=CF.
(1)求证:四边形EGFH是平行四边形;
(2)连接BD交AC于点O,若BD=14,AE+CF=EF,求EG的长.
【解】:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠GAE=∠HCF,
∵点G,H分别是AB,CD的中点,
∴AG=CH,
在△AGE和△CHF中,
, ∴△AGE≌△CHF(SAS),
∴GE=HF,∠AEG=∠CFH,
∴∠GEF=∠HFE,
∴GE∥HF,
又∵GE=HF,
∴四边形EGFH是平行四边形;
(2)解:连接BD交AC于点O,如图:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BD=14,
∴OB=OD=7,
∵AE=CF,OA=OC,
∴OE=OF,
∵AE+CF=EF,AE=CF,
∴2AE=EF=2OE,
∴AE=OE,
又∵点G是AB的中点,
∴EG是△ABO的中位线,
∴EG=OB=.
21.如图,在 ABCD中,AD>AB,∠ABC的平分线交AD于点F,EF∥AB交BC于点E.
(1)求证:四边形ABEF是菱形;
(2)若AB=5,AE=6, ABCD的面积为36,求CE的长.
【解】:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABEF是平行四边形,
∵BF平分∠ABC,
∴∠ABF=∠EBF,
∵AF∥BC,
∴∠AFB=∠FBE,
∴∠ABF=∠AFB,
∴AB=AF,
∴四边形ABEF是菱形;
(2)∵四边形ABEF是菱形,
∴AE⊥BF,AO=OE=3,BO=OF,AB=BE=5,
∴BO===4,
∴BF=8,
∴菱形ABEF的面积=×6×8=24,
∵AD∥BC,AB∥EF∥CD,
∴四边形ECDF是平行四边形,
∴ S EFDC=36﹣24=12,
∴ S菱形ABFE:S EFDC=2:1,
∴BE:EC=2:1,
∴EC=.
22.如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若OE=5,AE=3,求菱形ABCD的面积.
【解】:(1)四边形AEBO是矩形,理由如下:
∵BE∥AC,AE∥BD
∴四边形AEBO是平行四边形.
又∵菱形ABCD对角线交于点O
∴AC⊥BD,即∠AOB=90°.
∴四边形AEBO是矩形;
(2)∵四边形ABCD是菱形,
∴OA=AC,OB=BD,AC⊥BD,
∵四边形AEBO是矩形,
∴AB=OE=5,
∴OB=AE=3,
∴AO===4,
∴BD=2OB=6,AC=2AO=8,
∴菱形ABCD的面积=AC×BD=×8×6=24.
23.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:①CE与CG有怎样的位置关系?请说明理由.
②CE+CG的值为 2 .
【解】:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°﹣∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
, ∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)①CE⊥CG,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
, ∴△ADE≌△CDG(SAS),
∴∠CDA=∠DCG,
∵∠ACD+∠CAD+∠ADC=180°,∠ADC=90°,
∴∠ACG=∠ACD+∠DCG=∠ACD+∠CAD=90°,
∴CE⊥CG;
②由①知,△ADE≌△CDG,
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×=2,
第1页(共11页)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
