人教版七年级数学下册 第五章相交线与平行线 复习教学设计
文档属性
| 名称 | 人教版七年级数学下册 第五章相交线与平行线 复习教学设计 | 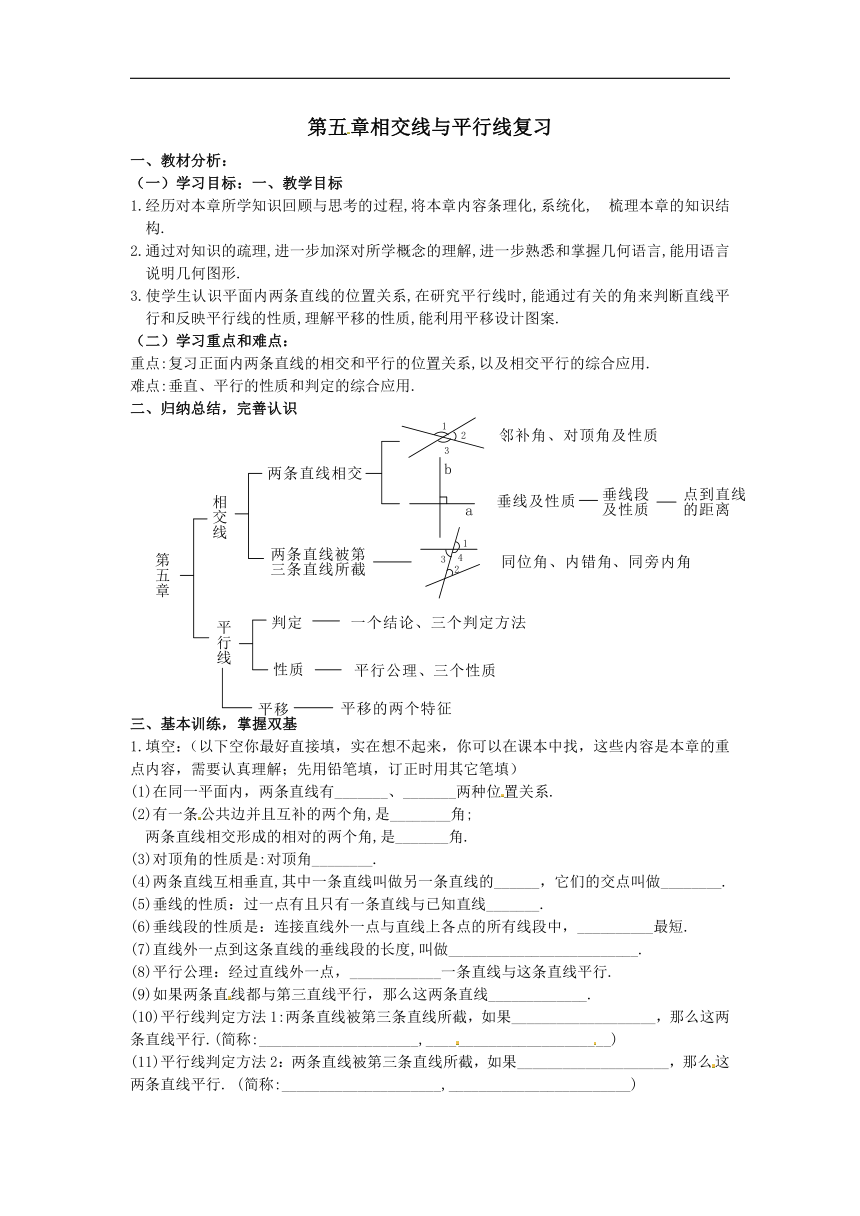 | |
| 格式 | doc | ||
| 文件大小 | 233.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 10:37:02 | ||
图片预览

文档简介
第五章相交线与平行线复习
一、教材分析:
(一)学习目标:一、教学目标
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
(二)学习重点和难点:
重点:复习正面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
难点:垂直、平行的性质和判定的综合应用.
二、归纳总结,完善认识
三、基本训练,掌握双基
1.填空:(以下空你最好直接填,实在想不起来,你可以在课本中找,这些内容是本章的重点内容,需要认真理解;先用铅笔填,订正时用其它笔填)
(1)在同一平面内,两条直线有_______、_______两种位置关系.
(2)有一条公共边并且互补的两个角,是________角;
两条直线相交形成的相对的两个角,是_______角.
(3)对顶角的性质是:对顶角________.
(4)两条直线互相垂直,其中一条直线叫做另一条直线的______,它们的交点叫做________.
(5)垂线的性质:过一点有且只有一条直线与已知直线_______.
(6)垂线段的性质是:连接直线外一点与直线上各点的所有线段中,__________最短.
(7)直线外一点到这条直线的垂线段的长度,叫做_________________________.
(8)平行公理:经过直线外一点,____________一条直线与这条直线平行.
(9)如果两条直线都与第三直线平行,那么这两条直线_____________.
(10)平行线判定方法1:两条直线被第三条直线所截,如果___________________,那么这两条直线平行.(简称:_____________________,________________________)
(11)平行线判定方法2:两条直线被第三条直线所截,如果____________________,那么这两条直线平行. (简称:_____________________,________________________)
(12)平行线判定方法3:两条直线被第三条直线所截,如果____________________,那么这两条直线平行. (简称:_____________________,________________________)
(13)平行线性质1:两条平行线被第三条直线所截, ______________________.
(14)平行线性质2:两条平行线被第三条直线所截, ______________________.
(15)平行线性质3:两条平行线被第三条直线所截, ______________________.
(16)判断一件事情的语句,叫做_________;判断正确的命题是______命题,判断错误的命题是______命题;经过推理得到的真命题叫做___________;命题常常可以写成“如果……那么……”的形式,“如果”后接的部分是_________,“那么”后接的部分是________.
(17)图形沿某一直线方向移动,叫做________;移动后的新图形与移动前的旧图形_________和_________相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段________且________.
2.判断题:对的画“√”,错的画“×”.
(1)有公共顶点且相等的两个角是对顶角. ( )
(2)如果两个角互补,那么它们是邻补角. ( )
(3)如果两个角是邻补角,那么它们互补. ( )
(4)两条直线相交构成的四个角中,如果有一个角是直角,那么其它三个角也是直角. ( )
(5)平行于同一条直线的两条直线平行. ( )
(6)同旁内角相等,两直线平行. ( )
(7)两条直线垂直于同一条直线,这两条直线平行.( )
(8)同位角相等. ( )
3.填空:
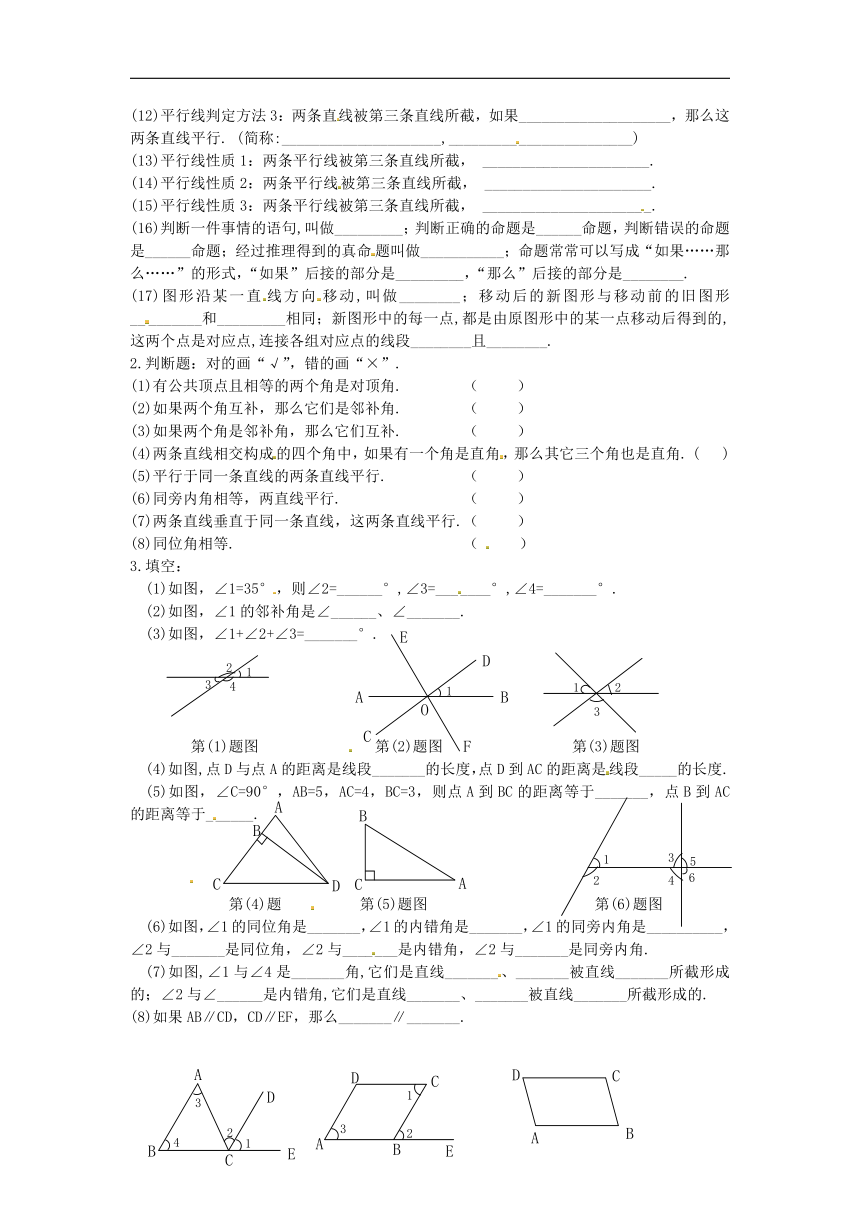
(1)如图,∠1=35°,则∠2=______°,∠3=_______°,∠4=_______°.
(2)如图,∠1的邻补角是∠______、∠_______.
(3)如图,∠1+∠2+∠3=_______°.
第(1)题图 第(2)题图 第(3)题图
(4)如图,点D与点A的距离是线段_______的长度,点D到AC的距离是线段_____的长度.
(5)如图,∠C=90°,AB=5,AC=4,BC=3,则点A到BC的距离等于_______,点B到AC的距离等于______.
第(4)题 第(5)题图 第(6)题图
(6)如图,∠1的同位角是_______,∠1的内错角是_______,∠1的同旁内角是__________,∠2与_______是同位角,∠2与_______是内错角,∠2与_______是同旁内角.
(7)如图,∠1与∠4是_______角,它们是直线_______、_______被直线_______所截形成的;∠2与∠______是内错角,它们是直线_______、_______被直线_______所截形成的.
(8)如果AB∥CD,CD∥EF,那么_______∥_______.
第(7)题图 第(9)题图 第(10)题图
(9)如图,如果∠2=∠3,那么_____∥______;如果∠1=∠2,那么_____∥_____.
(10)如图,如果∠A+∠B=180°,那么____∥_____;如果∠B+∠C=180°,那么____∥____.
(11)如图,AB∥CD,∠B=40°,则∠BED=______°,∠DEF=______°.
(12)如图,如果AB∥CD,那么∠______=∠______;如果AD∥BC,那么∠______=∠______.
(13)如图,已知a∥b,∠1=120°,∠2=_____°.
第(11)题图 第(12)题图 第(13)题图
(14)命题“几个负数相乘,积一定为正数”的题设是____________________,结论是______________________,这个命题是_______命题.(填“真”或“假”)
(15)命题“同角的补角相等”的题设是________________________________,结论是_______________________,这个命题是________命题.
4.作图题:
(1)用三角尺,过点P作线段AB的垂线. (2)用三角尺,作点A到直线l的垂线段AB.
(3)用直尺和三角尺,作过点O且平行于a的直线.
四、典型例题,加深理解
例1 完成下面的说理过程:
如图,已知∠1=∠2,说明∠1与∠3互补. 说理过程如下:
因为∠1=∠2,
所以________∥________( ).
所以∠1与∠3互补( ).
例2 如图,∠ADE=60°,∠B=60°,∠CED=140°.
求∠C的度数.(审题时把已知和求标到图中,在审题基础
上分析解题思路,在学生弄清思路的基础上,
按下面格式板演)
解:因为∠ADE=∠B=60°,
所以___∥____(______________,_________________).
所以∠C与∠CED互补(______________,_________________).
所以∠C=_____ _______=______-______=______°.
五、综合运用,发展能力
5.完成下面的说理过程:
如图,已知∠1=∠3,说明∠2+∠4=180°.
说理过程如下:
因为∠1=∠3,
所以______∥_______( ).
所以∠2+∠5=180°( ).
又因为∠4=∠5( ),
所以∠2+∠4=180°.
7.选作题:如图,AB∥CD∥EF,求∠BAC+∠ACE+∠CEF的度数.
第7题图
PAGE
一、教材分析:
(一)学习目标:一、教学目标
1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化, 梳理本章的知识结构.
2.通过对知识的疏理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,在研究平行线时,能通过有关的角来判断直线平行和反映平行线的性质,理解平移的性质,能利用平移设计图案.
(二)学习重点和难点:
重点:复习正面内两条直线的相交和平行的位置关系,以及相交平行的综合应用.
难点:垂直、平行的性质和判定的综合应用.
二、归纳总结,完善认识
三、基本训练,掌握双基
1.填空:(以下空你最好直接填,实在想不起来,你可以在课本中找,这些内容是本章的重点内容,需要认真理解;先用铅笔填,订正时用其它笔填)
(1)在同一平面内,两条直线有_______、_______两种位置关系.
(2)有一条公共边并且互补的两个角,是________角;
两条直线相交形成的相对的两个角,是_______角.
(3)对顶角的性质是:对顶角________.
(4)两条直线互相垂直,其中一条直线叫做另一条直线的______,它们的交点叫做________.
(5)垂线的性质:过一点有且只有一条直线与已知直线_______.
(6)垂线段的性质是:连接直线外一点与直线上各点的所有线段中,__________最短.
(7)直线外一点到这条直线的垂线段的长度,叫做_________________________.
(8)平行公理:经过直线外一点,____________一条直线与这条直线平行.
(9)如果两条直线都与第三直线平行,那么这两条直线_____________.
(10)平行线判定方法1:两条直线被第三条直线所截,如果___________________,那么这两条直线平行.(简称:_____________________,________________________)
(11)平行线判定方法2:两条直线被第三条直线所截,如果____________________,那么这两条直线平行. (简称:_____________________,________________________)
(12)平行线判定方法3:两条直线被第三条直线所截,如果____________________,那么这两条直线平行. (简称:_____________________,________________________)
(13)平行线性质1:两条平行线被第三条直线所截, ______________________.
(14)平行线性质2:两条平行线被第三条直线所截, ______________________.
(15)平行线性质3:两条平行线被第三条直线所截, ______________________.
(16)判断一件事情的语句,叫做_________;判断正确的命题是______命题,判断错误的命题是______命题;经过推理得到的真命题叫做___________;命题常常可以写成“如果……那么……”的形式,“如果”后接的部分是_________,“那么”后接的部分是________.
(17)图形沿某一直线方向移动,叫做________;移动后的新图形与移动前的旧图形_________和_________相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段________且________.
2.判断题:对的画“√”,错的画“×”.
(1)有公共顶点且相等的两个角是对顶角. ( )
(2)如果两个角互补,那么它们是邻补角. ( )
(3)如果两个角是邻补角,那么它们互补. ( )
(4)两条直线相交构成的四个角中,如果有一个角是直角,那么其它三个角也是直角. ( )
(5)平行于同一条直线的两条直线平行. ( )
(6)同旁内角相等,两直线平行. ( )
(7)两条直线垂直于同一条直线,这两条直线平行.( )
(8)同位角相等. ( )
3.填空:
(1)如图,∠1=35°,则∠2=______°,∠3=_______°,∠4=_______°.
(2)如图,∠1的邻补角是∠______、∠_______.
(3)如图,∠1+∠2+∠3=_______°.
第(1)题图 第(2)题图 第(3)题图
(4)如图,点D与点A的距离是线段_______的长度,点D到AC的距离是线段_____的长度.
(5)如图,∠C=90°,AB=5,AC=4,BC=3,则点A到BC的距离等于_______,点B到AC的距离等于______.
第(4)题 第(5)题图 第(6)题图
(6)如图,∠1的同位角是_______,∠1的内错角是_______,∠1的同旁内角是__________,∠2与_______是同位角,∠2与_______是内错角,∠2与_______是同旁内角.
(7)如图,∠1与∠4是_______角,它们是直线_______、_______被直线_______所截形成的;∠2与∠______是内错角,它们是直线_______、_______被直线_______所截形成的.
(8)如果AB∥CD,CD∥EF,那么_______∥_______.
第(7)题图 第(9)题图 第(10)题图
(9)如图,如果∠2=∠3,那么_____∥______;如果∠1=∠2,那么_____∥_____.
(10)如图,如果∠A+∠B=180°,那么____∥_____;如果∠B+∠C=180°,那么____∥____.
(11)如图,AB∥CD,∠B=40°,则∠BED=______°,∠DEF=______°.
(12)如图,如果AB∥CD,那么∠______=∠______;如果AD∥BC,那么∠______=∠______.
(13)如图,已知a∥b,∠1=120°,∠2=_____°.
第(11)题图 第(12)题图 第(13)题图
(14)命题“几个负数相乘,积一定为正数”的题设是____________________,结论是______________________,这个命题是_______命题.(填“真”或“假”)
(15)命题“同角的补角相等”的题设是________________________________,结论是_______________________,这个命题是________命题.
4.作图题:
(1)用三角尺,过点P作线段AB的垂线. (2)用三角尺,作点A到直线l的垂线段AB.
(3)用直尺和三角尺,作过点O且平行于a的直线.
四、典型例题,加深理解
例1 完成下面的说理过程:
如图,已知∠1=∠2,说明∠1与∠3互补. 说理过程如下:
因为∠1=∠2,
所以________∥________( ).
所以∠1与∠3互补( ).
例2 如图,∠ADE=60°,∠B=60°,∠CED=140°.
求∠C的度数.(审题时把已知和求标到图中,在审题基础
上分析解题思路,在学生弄清思路的基础上,
按下面格式板演)
解:因为∠ADE=∠B=60°,
所以___∥____(______________,_________________).
所以∠C与∠CED互补(______________,_________________).
所以∠C=_____ _______=______-______=______°.
五、综合运用,发展能力
5.完成下面的说理过程:
如图,已知∠1=∠3,说明∠2+∠4=180°.
说理过程如下:
因为∠1=∠3,
所以______∥_______( ).
所以∠2+∠5=180°( ).
又因为∠4=∠5( ),
所以∠2+∠4=180°.
7.选作题:如图,AB∥CD∥EF,求∠BAC+∠ACE+∠CEF的度数.
第7题图
PAGE
