人教版七年级数学下册7.1.2平面直角坐标系 教案
文档属性
| 名称 | 人教版七年级数学下册7.1.2平面直角坐标系 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 949.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 11:31:10 | ||
图片预览

文档简介
7.1.2平面直角坐标系
教学目标
1、使学生理解平面直角坐标系的有关概念,并会正确地画出平面直角坐标系。
2、使学生理解平面内点的坐标的意义,会根据坐标确定点和由点求得坐标。、
重点、难点
重点:1、能正确地画出平面直角坐标系。
2、能在平面直角坐标系中,根据坐标找出点,由点求得坐标。
难点:在平面直角坐标系中,根据坐标找出点由点求出坐标。
教学过程
一、复习导入
数轴上的点可以用什么来表示?
可以用一个数来表示,我们把这个数叫做这个点的坐标。
如图,数轴上的点A可以用-4来表示,-4对应数轴上的点A,那么就说点A的坐标是-4.
你能确定B点的坐标么?
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
设计意图:利用复习导入,让学生回顾旧知识的同时将新知识纳入自己的认知体系做好铺垫,使学生认识到数学知识来源于生活,应用于生活,激发他们的求知欲望。
二、探究新知
1、导入:类似于利用数轴确定直线上点的位置,结合上节课学习的有序数对,回答问题:
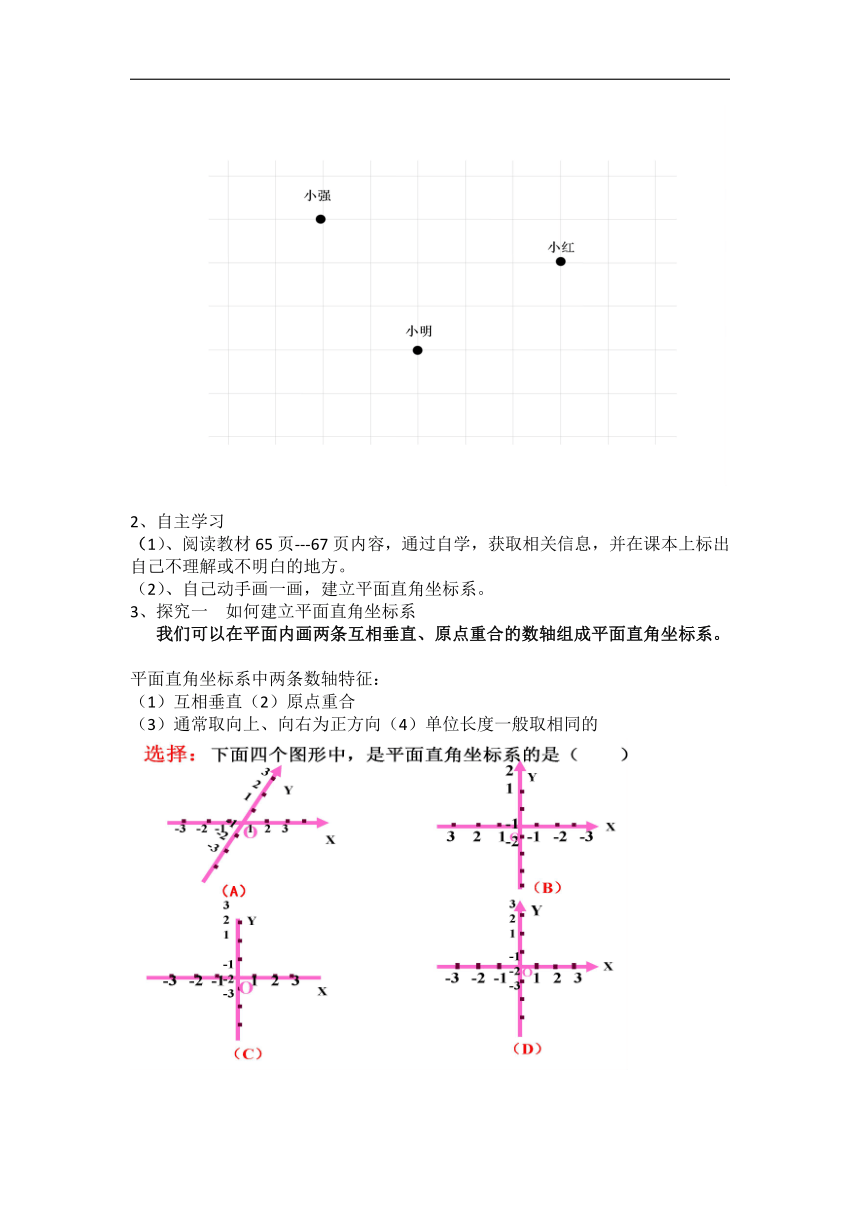
如图:你能找到一种办法来确定平面内小强、小红、小明的位置吗?
2、自主学习
(1)、阅读教材65页---67页内容,通过自学,获取相关信息,并在课本上标出自己不理解或不明白的地方。
(2)、自己动手画一画,建立平面直角坐标系。
3、探究一 如何建立平面直角坐标系
我们可以在平面内画两条互相垂直、原点重合的数轴组成平面直角坐标系。
平面直角坐标系中两条数轴特征:
(1)互相垂直(2)原点重合
(3)通常取向上、向右为正方向(4)单位长度一般取相同的
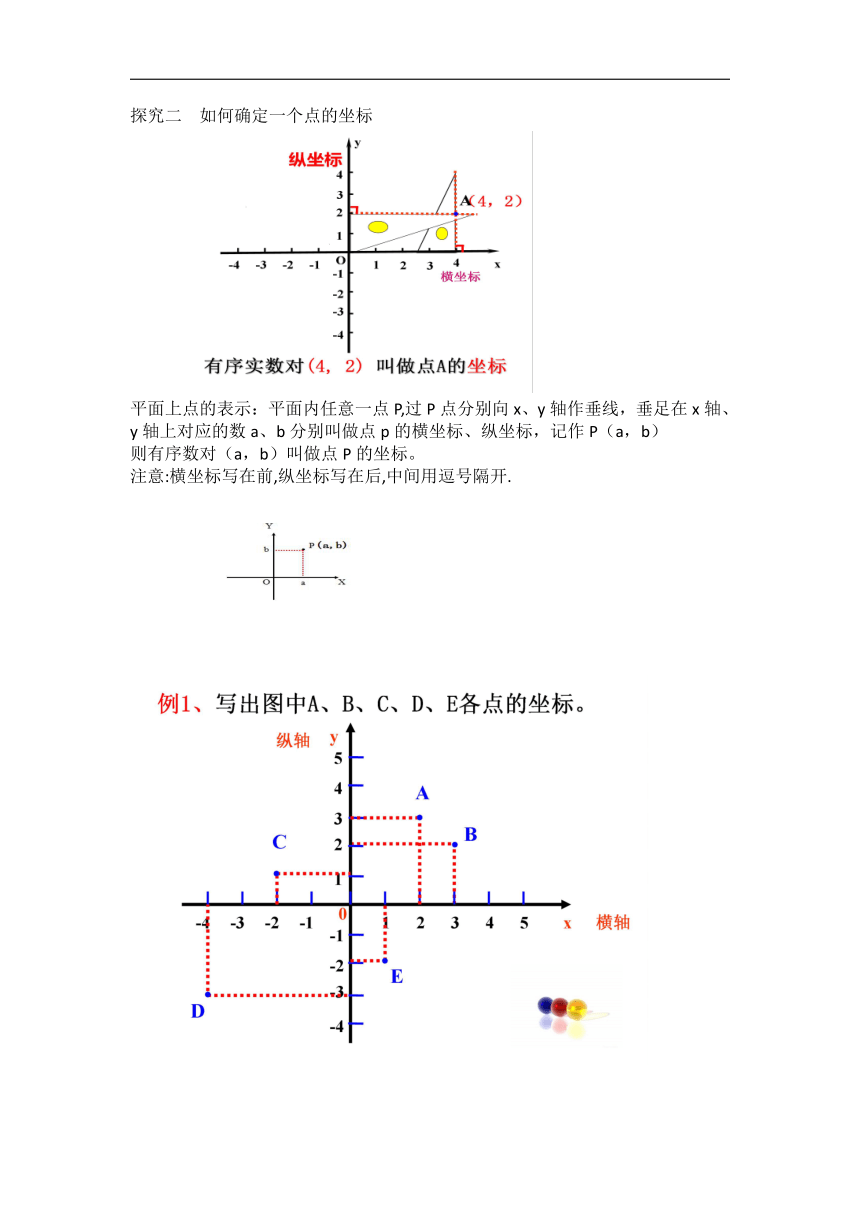
探究二 如何确定一个点的坐标
平面上点的表示:平面内任意一点P,过P点分别向x、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点p的横坐标、纵坐标,记作P(a,b)
则有序数对(a,b)叫做点P的坐标。
注意:横坐标写在前,纵坐标写在后,中间用逗号隔开.
学生在自己画好的平面直角坐标系内描点。
A(-5,2) B (3,-2) C(0,4)
D(-6,0) E(1,2) F (-6,-4)
总结:平面内的点与有序实数对之间是一一对应的。
例2.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
思考与总结:原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
学生首先独立完成问题,在此过程中教师要关注:学生能否按照要求正确画图并准确标记有序数对;对于学有困难的学生,教师要给予具体的帮助、鼓励和指导,使全班同学都能积极参与。
问题:建立了平面直角坐标系后,平面就被两条数轴分成几个部分?如何称呼?
思考:各个象限的点的坐标分别有什么特点?
考考你:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) ; B(3,-2); C(0,4); D(-6,0);
E(1,8); F(0,0); G(5,0); H(-6,-4); K(0,-3).
1、写出图中多边形ABCDEF各个顶点的坐标。
2、点B与点C的纵坐标有什么特点,线段BC的位置 有什么特点?
3、线段CE的位置 有什么特点?
总结:特殊位置的点的符号特征
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
三、课堂练习:
1、在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
2、平面内点的坐标是( )
A、一个点 B、一个图形
C、一个实数 D、一对有序实数
3.如图1所示,点A的坐标是 ( )
A.(3,2); B.(3,3);
C.(3,-3); D.(-3,-3)
4.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B
C.点C D.点D
5、点P的坐标为(a+3,2a-4).
若P在x轴上,则a=______;
若P在y轴上,则a=______.
6、已知点A(x,y).
(1)若xy=0,则点A在___________;
(2)若xy>0,则点A在___________;
(3)若xy<0,则点A在___________.
四、课堂小结:
本节课你学到了什么?
五、布置作业:
课本68页:练习1~2题
教学目标
1、使学生理解平面直角坐标系的有关概念,并会正确地画出平面直角坐标系。
2、使学生理解平面内点的坐标的意义,会根据坐标确定点和由点求得坐标。、
重点、难点
重点:1、能正确地画出平面直角坐标系。
2、能在平面直角坐标系中,根据坐标找出点,由点求得坐标。
难点:在平面直角坐标系中,根据坐标找出点由点求出坐标。
教学过程
一、复习导入
数轴上的点可以用什么来表示?
可以用一个数来表示,我们把这个数叫做这个点的坐标。
如图,数轴上的点A可以用-4来表示,-4对应数轴上的点A,那么就说点A的坐标是-4.
你能确定B点的坐标么?
类似于利用数轴确定直线上点的位置,能不能找到一种办法来确定平面内的点的位置呢?
设计意图:利用复习导入,让学生回顾旧知识的同时将新知识纳入自己的认知体系做好铺垫,使学生认识到数学知识来源于生活,应用于生活,激发他们的求知欲望。
二、探究新知
1、导入:类似于利用数轴确定直线上点的位置,结合上节课学习的有序数对,回答问题:
如图:你能找到一种办法来确定平面内小强、小红、小明的位置吗?
2、自主学习
(1)、阅读教材65页---67页内容,通过自学,获取相关信息,并在课本上标出自己不理解或不明白的地方。
(2)、自己动手画一画,建立平面直角坐标系。
3、探究一 如何建立平面直角坐标系
我们可以在平面内画两条互相垂直、原点重合的数轴组成平面直角坐标系。
平面直角坐标系中两条数轴特征:
(1)互相垂直(2)原点重合
(3)通常取向上、向右为正方向(4)单位长度一般取相同的
探究二 如何确定一个点的坐标
平面上点的表示:平面内任意一点P,过P点分别向x、y轴作垂线,垂足在x轴、y轴上对应的数a、b分别叫做点p的横坐标、纵坐标,记作P(a,b)
则有序数对(a,b)叫做点P的坐标。
注意:横坐标写在前,纵坐标写在后,中间用逗号隔开.
学生在自己画好的平面直角坐标系内描点。
A(-5,2) B (3,-2) C(0,4)
D(-6,0) E(1,2) F (-6,-4)
总结:平面内的点与有序实数对之间是一一对应的。
例2.在下面直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
思考与总结:原点O的坐标是什么?x轴和y轴上的点的坐标有什么特点?
学生首先独立完成问题,在此过程中教师要关注:学生能否按照要求正确画图并准确标记有序数对;对于学有困难的学生,教师要给予具体的帮助、鼓励和指导,使全班同学都能积极参与。
问题:建立了平面直角坐标系后,平面就被两条数轴分成几个部分?如何称呼?
思考:各个象限的点的坐标分别有什么特点?
考考你:请你根据下列各点的坐标判定它们分别在第几象限或在什么坐标轴上?
A(-5,2) ; B(3,-2); C(0,4); D(-6,0);
E(1,8); F(0,0); G(5,0); H(-6,-4); K(0,-3).
1、写出图中多边形ABCDEF各个顶点的坐标。
2、点B与点C的纵坐标有什么特点,线段BC的位置 有什么特点?
3、线段CE的位置 有什么特点?
总结:特殊位置的点的符号特征
平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
横轴上的点纵坐标为0;纵轴上的点横坐标为0。
三、课堂练习:
1、在平面直角坐标系内,下列各点在第四象限的是( )
A.(2,1) B.(-2,1) C.(-3,-5) D.(3,-5)
2、平面内点的坐标是( )
A、一个点 B、一个图形
C、一个实数 D、一对有序实数
3.如图1所示,点A的坐标是 ( )
A.(3,2); B.(3,3);
C.(3,-3); D.(-3,-3)
4.如图1所示,坐标是(-2,2)的点是 ( )
A.点A B.点B
C.点C D.点D
5、点P的坐标为(a+3,2a-4).
若P在x轴上,则a=______;
若P在y轴上,则a=______.
6、已知点A(x,y).
(1)若xy=0,则点A在___________;
(2)若xy>0,则点A在___________;
(3)若xy<0,则点A在___________.
四、课堂小结:
本节课你学到了什么?
五、布置作业:
课本68页:练习1~2题
