人教版七年级数学下册5.3平行线的判定与性质的综合应用 教学设计 (表格式)
文档属性
| 名称 | 人教版七年级数学下册5.3平行线的判定与性质的综合应用 教学设计 (表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 00:00:00 | ||
图片预览


文档简介
5.3.2 平行线的判定与性质的综合应用
教学目标:
1、知识与技能目标:
(1)、巩固平行线的判定与性质定理,及其图形语言和符号语言;
(2)、会利用平行线的判定与性质进行简单的推理,从而培养学生的分析推理能力.
2 、过程与方法目标:
通过审题、思考、交流、展示等活动,明确结合证明题的解题思路,体会数形结合思想与转化思想的应用;培养学生审题、分析、推理能力,发展学生智能,深化学生思维能力和综合运用能力;渗透数学建模思想。
3、情感态度与价值观目标:
激发学生的求知欲,增强应用数学的意识,体会数学的价值,提高学习能力和合作精神,享受成功的喜悦。在推理证明的书写过程中,体会数学符号语言的精简之美。
教学重难点
巩固平行线的判定与性质定理,及其图形语言和符号语言
学情分析:
七年级学生刚刚跨入初中,依然保留着小学生的天真活泼、对新生事物很感兴趣、求知欲望强、具有强烈的好奇心与求知欲,形象直观思维已比较成熟,但推理能力还比较薄弱,对数形结合思想刚有初步认识,安排本节课是让学生进一步体会数形结合思想的应用及解题思路的逐步形成。
教学内容分析:
本节课是在学行线的判定及性质定理的基础上,综合应用以上知识解决相关问题,主要体会数形结合思想在几何教学中的应用。
教学过程(表格描述)
教学阶段 教学内容 师生活动 设置意图
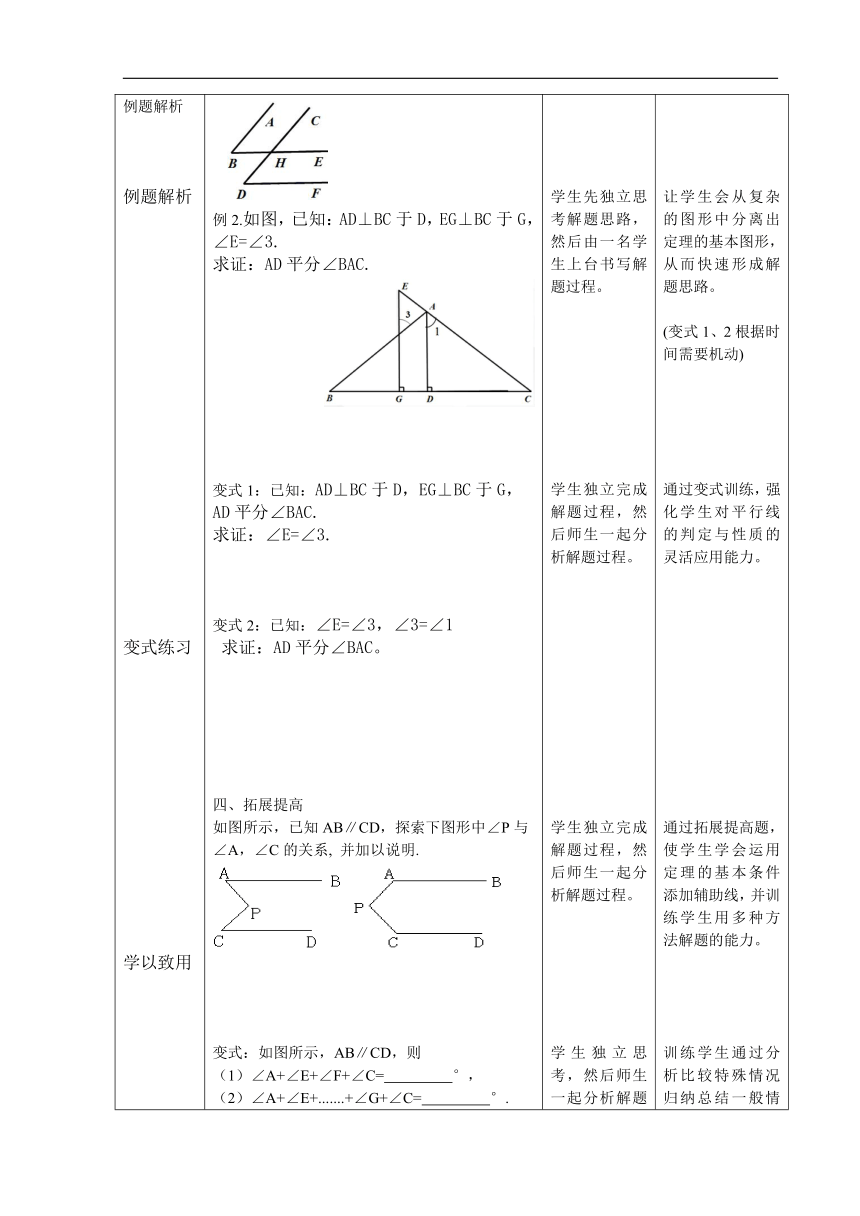
基础训练(知识回顾)例题解析例题解析变式练习学以致用学以致用拓展提高归纳总结课堂检测 一、知识回顾(习题复习)1、填空:已知:如图(1)∵AD∥BC∴∠1=∠B( )(2) ∵BE∥DC∴∠B+∠ =180°( )(3)∵AB∥CD,∴∠3= ( )(4)∵∠2=∠4,∴ ∥ ( )(5) ∵∠ =∠1,∴ ∥ (同位角相等,两直线平行)(6) ∵∠BCD+∠ =180°, ∴ ∥ ( )2. 已知:AB∥CD, ∠ABE=70°,则∠C= °.3.已知:AB∥CD,且CB平分∠ECD,∠1=30°,则∠B= °, ∠2= °.4.如图,能判断EB∥AC的条件是 (填序号).∠C=∠ABE,∠A=∠ABE,∠C=∠ABC,④∠C=∠EBD,⑤∠C+∠EBC=180°,⑥∠A=∠EBD. 三、例题解析例1、已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF。例2.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠3.求证:AD平分∠BAC.变式1:已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC.求证:∠E=∠3.变式2:已知:∠E=∠3,∠3=∠1求证:AD平分∠BAC。 四、拓展提高如图所示,已知AB∥CD,探索下图形中∠P与∠A,∠C的关系,并加以说明. 变式:如图所示,AB∥CD,则(1)∠A+∠E+∠F+∠C= °,(2)∠A+∠E+.......+∠G+∠C= °. n个角 (1)(2)五、课堂小结:1. 由已知,想可知;2. 由要证,想需证;3. 由角相等或角互补,想线平行;4. 由线平行,想角相等或角互补.课堂检测:1. 如图,AB∥EF,∠ECD=∠E,则CD∥AB.说理如下: 因为∠ECD=∠E, 所以CD∥EF( ). 又AB∥EF, 所以CD∥AB( ). 2.如图,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF. 3. 如图,已知:∠1=∠2,求证:∠3+∠4=180o. 4. 如图,已知:AB∥CD,∠A=∠C,求证:AD∥BC.5. 如图,已知AB∥CD,∠B=115°, ∠C=45°, 求 ∠BEC的度数. 6. 如图,已知:AB ∥CD,MG平分∠AMN,NH平分∠DNM,求证:MG∥NH. 学生回答,并讲解思路及依据。学生独立完成解题过程,然后一名学生讲解解题过程。学生先独立思考解题思路,然后由一名学生上台书写解题过程。学生独立完成解题过程,然后师生一起分析解题过程。学生独立完成解题过程,然后师生一起分析解题过程。学生独立思考,然后师生一起分析解题过程。总结收获(包括知识与方法两方面)独立解答,查漏补缺 。通过基础训练,进一步了解学生对定理的简单应用掌握情况为下面的应用做好铺垫。。训练学生简单的推理能力,及分析讲解能力让学生会从复杂的图形中分离出定理的基本图形,从而快速形成解题思路。(变式1、2根据时间需要机动)通过变式训练,强化学生对平行线的判定与性质的灵活应用能力。通过拓展提高题,使学生学会运用定理的基本条件添加辅助线,并训练学生用多种方法解题的能力。训练学生通过分析比较特殊情况归纳总结一般情况的能力, 让学生学有所得,把知识得以提升。通过检测了解学生的掌握情况,及时查漏补缺。
PAGE
教学目标:
1、知识与技能目标:
(1)、巩固平行线的判定与性质定理,及其图形语言和符号语言;
(2)、会利用平行线的判定与性质进行简单的推理,从而培养学生的分析推理能力.
2 、过程与方法目标:
通过审题、思考、交流、展示等活动,明确结合证明题的解题思路,体会数形结合思想与转化思想的应用;培养学生审题、分析、推理能力,发展学生智能,深化学生思维能力和综合运用能力;渗透数学建模思想。
3、情感态度与价值观目标:
激发学生的求知欲,增强应用数学的意识,体会数学的价值,提高学习能力和合作精神,享受成功的喜悦。在推理证明的书写过程中,体会数学符号语言的精简之美。
教学重难点
巩固平行线的判定与性质定理,及其图形语言和符号语言
学情分析:
七年级学生刚刚跨入初中,依然保留着小学生的天真活泼、对新生事物很感兴趣、求知欲望强、具有强烈的好奇心与求知欲,形象直观思维已比较成熟,但推理能力还比较薄弱,对数形结合思想刚有初步认识,安排本节课是让学生进一步体会数形结合思想的应用及解题思路的逐步形成。
教学内容分析:
本节课是在学行线的判定及性质定理的基础上,综合应用以上知识解决相关问题,主要体会数形结合思想在几何教学中的应用。
教学过程(表格描述)
教学阶段 教学内容 师生活动 设置意图
基础训练(知识回顾)例题解析例题解析变式练习学以致用学以致用拓展提高归纳总结课堂检测 一、知识回顾(习题复习)1、填空:已知:如图(1)∵AD∥BC∴∠1=∠B( )(2) ∵BE∥DC∴∠B+∠ =180°( )(3)∵AB∥CD,∴∠3= ( )(4)∵∠2=∠4,∴ ∥ ( )(5) ∵∠ =∠1,∴ ∥ (同位角相等,两直线平行)(6) ∵∠BCD+∠ =180°, ∴ ∥ ( )2. 已知:AB∥CD, ∠ABE=70°,则∠C= °.3.已知:AB∥CD,且CB平分∠ECD,∠1=30°,则∠B= °, ∠2= °.4.如图,能判断EB∥AC的条件是 (填序号).∠C=∠ABE,∠A=∠ABE,∠C=∠ABC,④∠C=∠EBD,⑤∠C+∠EBC=180°,⑥∠A=∠EBD. 三、例题解析例1、已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF。例2.如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠3.求证:AD平分∠BAC.变式1:已知:AD⊥BC于D,EG⊥BC于G,AD平分∠BAC.求证:∠E=∠3.变式2:已知:∠E=∠3,∠3=∠1求证:AD平分∠BAC。 四、拓展提高如图所示,已知AB∥CD,探索下图形中∠P与∠A,∠C的关系,并加以说明. 变式:如图所示,AB∥CD,则(1)∠A+∠E+∠F+∠C= °,(2)∠A+∠E+.......+∠G+∠C= °. n个角 (1)(2)五、课堂小结:1. 由已知,想可知;2. 由要证,想需证;3. 由角相等或角互补,想线平行;4. 由线平行,想角相等或角互补.课堂检测:1. 如图,AB∥EF,∠ECD=∠E,则CD∥AB.说理如下: 因为∠ECD=∠E, 所以CD∥EF( ). 又AB∥EF, 所以CD∥AB( ). 2.如图,已知:AB∥DE,∠ABC+∠DEF=180°, 求证:BC∥EF. 3. 如图,已知:∠1=∠2,求证:∠3+∠4=180o. 4. 如图,已知:AB∥CD,∠A=∠C,求证:AD∥BC.5. 如图,已知AB∥CD,∠B=115°, ∠C=45°, 求 ∠BEC的度数. 6. 如图,已知:AB ∥CD,MG平分∠AMN,NH平分∠DNM,求证:MG∥NH. 学生回答,并讲解思路及依据。学生独立完成解题过程,然后一名学生讲解解题过程。学生先独立思考解题思路,然后由一名学生上台书写解题过程。学生独立完成解题过程,然后师生一起分析解题过程。学生独立完成解题过程,然后师生一起分析解题过程。学生独立思考,然后师生一起分析解题过程。总结收获(包括知识与方法两方面)独立解答,查漏补缺 。通过基础训练,进一步了解学生对定理的简单应用掌握情况为下面的应用做好铺垫。。训练学生简单的推理能力,及分析讲解能力让学生会从复杂的图形中分离出定理的基本图形,从而快速形成解题思路。(变式1、2根据时间需要机动)通过变式训练,强化学生对平行线的判定与性质的灵活应用能力。通过拓展提高题,使学生学会运用定理的基本条件添加辅助线,并训练学生用多种方法解题的能力。训练学生通过分析比较特殊情况归纳总结一般情况的能力, 让学生学有所得,把知识得以提升。通过检测了解学生的掌握情况,及时查漏补缺。
PAGE
