青岛版八年级数学下册 第十章 一次函数 复习课件 (共24张PPT)
文档属性
| 名称 | 青岛版八年级数学下册 第十章 一次函数 复习课件 (共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 841.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 14:48:28 | ||
图片预览




文档简介
(共24张PPT)
第十章 一次函数
做一做
1.设下列两个函数当 x = x1时,y = y1;
当x = x 2时,y = y2,用“<”或“>”号填空
①对于函数y= x,若x2>x1,则y2___y1
②对于函数y= - x+3,若x2___x1,则y23
4
1
2
>
>
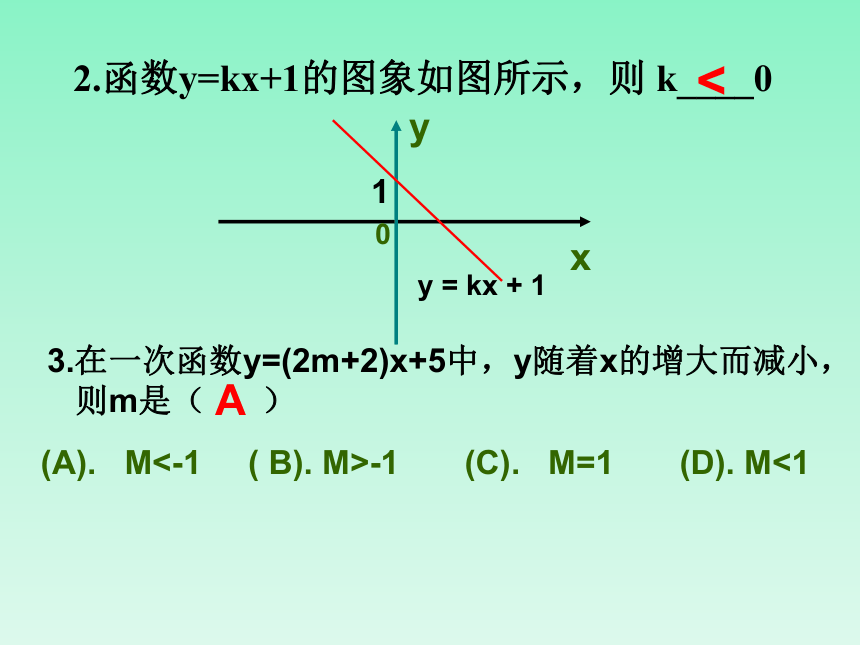
2.函数y=kx+1的图象如图所示,则 k____0
x
y
1
0
<
y = kx + 1
3.在一次函数y=(2m+2)x+5中,y随着x的增大而减小,
则m是( )
(A). M<-1 ( B). M>-1 (C). M=1 (D). M<1
A
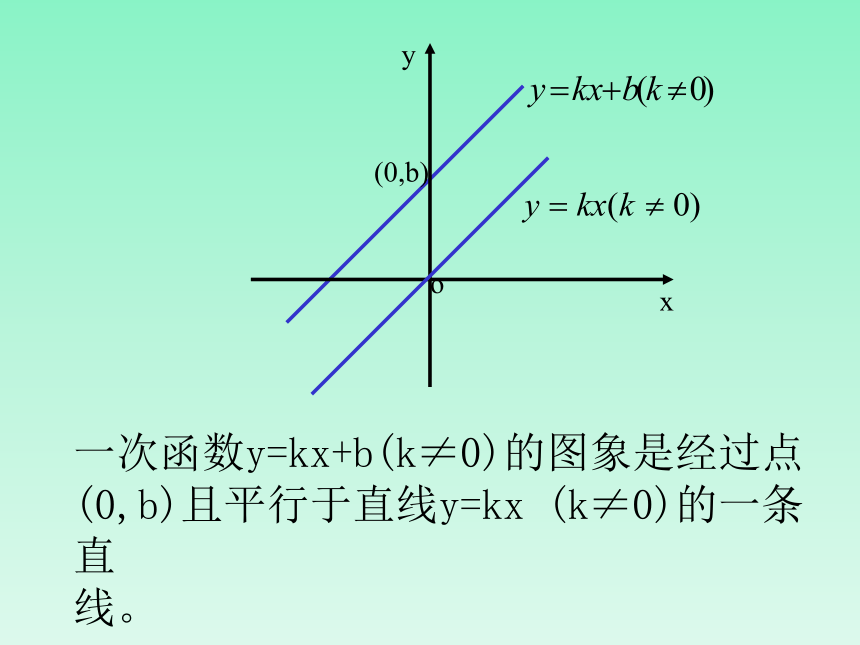
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直
线。
(0,b)
x
y
o
y=2x+1
x
y
o
y=2x
x
y
o
y=2x
y=2x-1
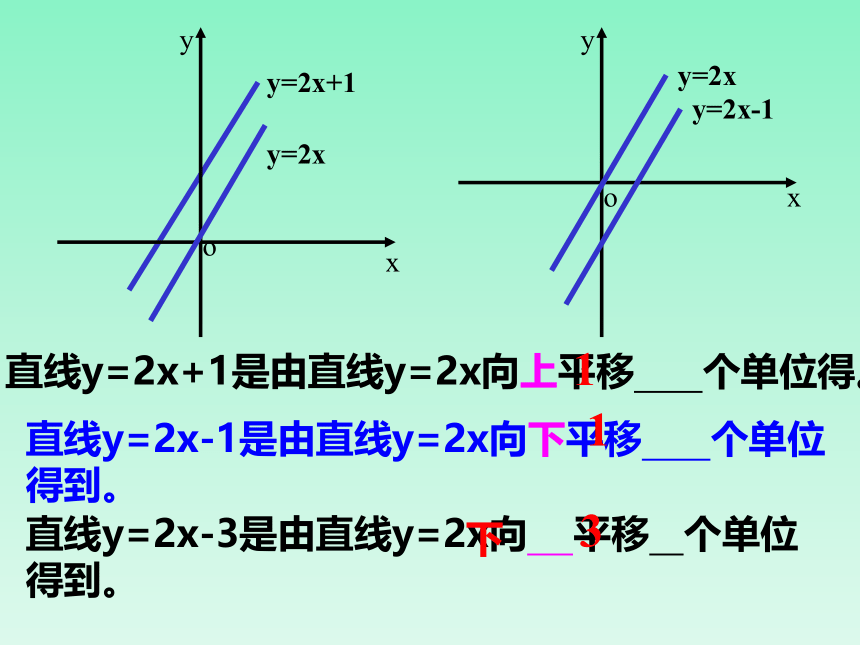
直线y=2x+1是由直线y=2x向上平移 个单位得。
直线y=2x-1是由直线y=2x向下平移 个单位得到。
1
1
直线y=2x-3是由直线y=2x向 平移 个单位得到。
下
3
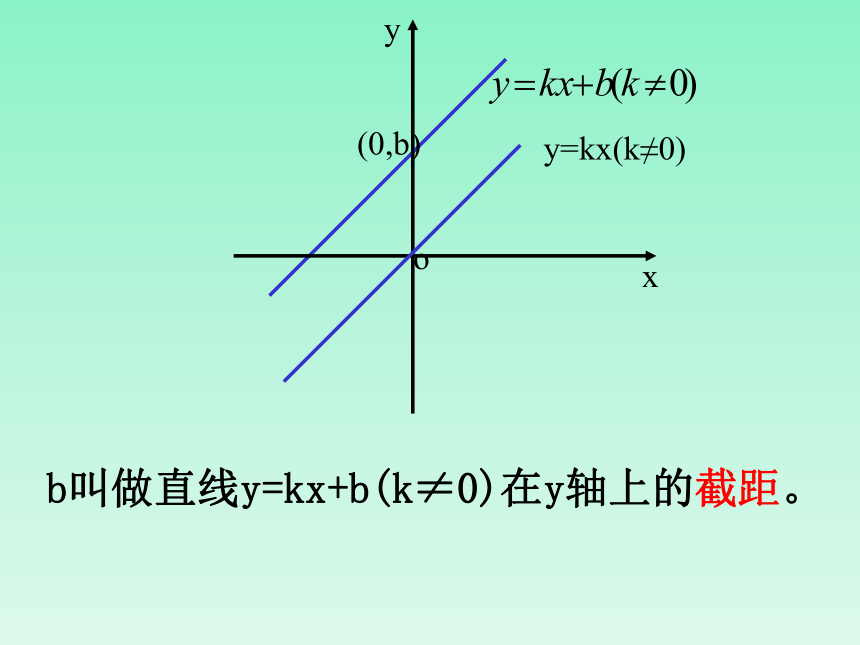
b叫做直线y=kx+b(k≠0)在y轴上的截距。
(0,b)
x
y
o
y=kx(k≠0)
(0,b)
x
y
o
(0,b)
直线
与x轴交点
与y轴交点
y=x+1
y=3x+1
y=-2x-1
y=-3-2x
(0,1)
(0,1)
(0,-1)
(0,-3)
(-3/2,0)
( -1/3,0)
(-1,0)
( -1/2,0)
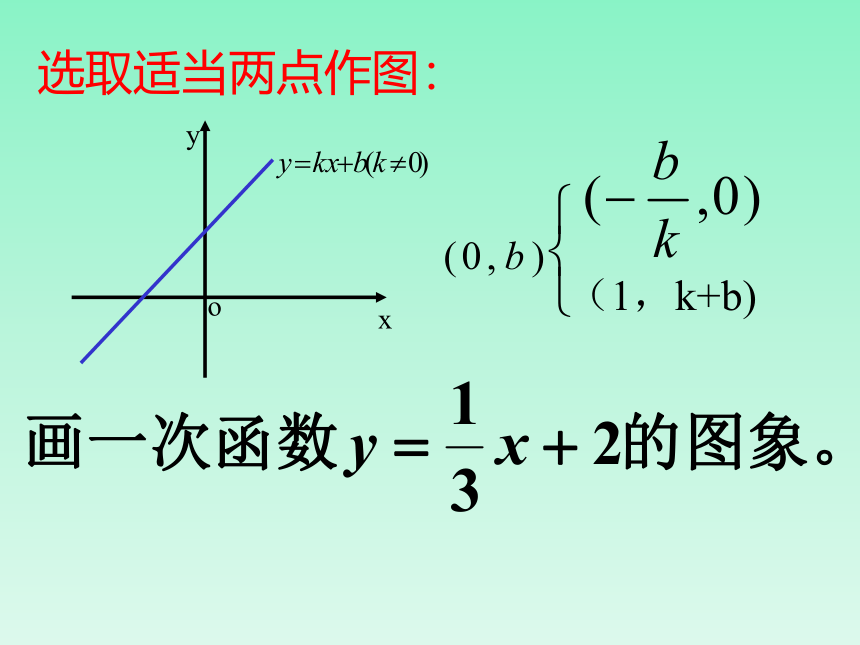
选取适当两点作图:
(1,k+b)
x
y
o
(1)对于函数y=-2x+5,当-1(2)对于函数y=2x+7, 当x1≤x≤x2, _____ ≤ y ≤ _____
1
7
2x1+7
2x2+7
(3)已知y是关于x的一次 函数,这个函数的图象经过
A(0,-8),B(1,2)两点,求当1函数值y的变化范围
数形结合训练:
1、已知一次函数y=kx+b(k≠0)平行于
直线y=3x,且过点(1,4),求函数解析式。
2、已知一次函数y=kx+b(k≠0)在y轴上
的截距是-2,且过点(1,3),求函数解析式。
函数解析式为:y=3x+1
函数解析式为:y=5x-2
3、看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。
o
x
y
o
x
y
o
x
y
k<0
b<0
k>0
b>0
k<0
b=0
4、已知一次函数y=kx+b(k≠0)中
①k>0,b<0 ②k<0,b>0,试作草图。
o
y
x
o
y
x
利用函数图象解一次函数应用题
一、热身练习
1、已知一次函数图象过点(1,2),(2,3)
求这个一次函数解析式;
2、如图,折线ABCDE描述汽车在某一直线公路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
其中正确的说法共有( )
A、1个 B、2个 C、3个 D、0个
×
√
×
A
温馨提示:
仔细观察图象,
捕捉有效信息!
你还有什么说法?
0
1
2
销售(万件)
800
1300
收入(元)
3、志成公司营销人员的个人收入与每月的销售业绩满足一次函数关系,图象如图所示,由图中的信息可知:营销人员没有销售业绩时的收入是______元。
300
决定一、三象限
k
决定二、四象限
b
决定二、四象限
k
决定一、三象限
b
当k>0时
o
x
y
o
y
x
o
y
x
y
o
x
当k<0时
1、一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
4、选取适当两点作图:
(1,k+b)
2、
3、
中考范例
(哈尔滨)如图,表示一轮船和一快艇沿相同路线,从甲港
到乙港行驶过程中路程随时间变化的图象,解答下列问题:
(1)分别求出表示轮船和快艇行驶过程的函数解析式;
(2)轮船和快艇在途中行驶速度分别是多少
(3) 快艇出发多长时间赶上轮船
解:(1)设轮船行驶过程的函数解析式为y=kx, 由图象知:当x=8时,y=160.
∴8k=160, 解得k=20.
∴轮船行驶过程的函数解析式为y=20x.
设快艇行驶过程的函数解析式为 y=kx+b.
由图象知:当x=2时,y=0; 当x=6时,y=160. 解得k=40,b=-80 ∴快艇行驶过程的函数解析式为y=40x-80.
(2)由图象知,
轮船在8h内行驶160km,
快艇在4h内行驶160km,
轮船行驶速度为20(km/h),
快艇行驶速度为40(km/h)
(3)设轮船出发x小时被快艇赶上。
20x=40x-80,x=4,
∴x-2=4-2=2.
答:快艇出发2小时赶上轮船.
y
x
你还可以设计哪些问题?
1、由于经济和社会发展迅速,用电矛盾越来越突出,为缓
解用电紧张,电力公司制定了新的用电收费标准,每月用
电量x(度)与应付电费y(元)的关系如图所示。
⑴请你根据图像所描述的信息,分别求0≤x≤50和x>50时,
y与x函数关系式。
⑵根据你的分析:
当每月用电量不超过50度时,
收费标准是________;
当每月的用电量超过50度时,
收费标准是______________
_______________________
____________.
当堂练习
y=0.5x (0≤x≤50) ;
=0.9x-20 (x>50).
0.5元/度
不超过50度部分
按0.5元/度计算,超过部分
按0.9元/度计算
2、某单位急需用车,准备和个体车主或租车公司签订月租车合同,设汽车每月行驶x千米,付个体车主的月费用y1元,出租公司的月租费是y2元,图象如图,观察图象回答:
(1)每月行驶的路程
在什么范围内时,
租公司的车合算?
(2)每月行驶的路程
等于多少时,租两家
的费用相同?
(3)如果这个单位估
计每月行驶的路程为
2300千米,那么租哪
一家的车合算?
观察函数图象,并根据你所获得的信息回答问题:
1、折线CAB表示某个实际问题的函数图象,请你编写一道符合该图象意义的应用题;
2、根据你所给出的应用题分别指出x轴、y轴所表示的意义,并写出C、A、B的坐标;
3、求图象AB的函数解析式,注明自变量x取值范围。
y
x
O
A
B
合作编题
C
数与形,相倚依,焉能分作两边飞?
数缺形时少直观,形少数时难入微,
数形结合百般好,隔裂分家万事非,
切莫忘,几何代数统一体,
永远联系、切莫分离!
——我国著名的数学家华罗庚
写一篇与“数形结合”有关的数学小论文,交流展览。
第十章 一次函数
做一做
1.设下列两个函数当 x = x1时,y = y1;
当x = x 2时,y = y2,用“<”或“>”号填空
①对于函数y= x,若x2>x1,则y2___y1
②对于函数y= - x+3,若x2___x1,则y2
4
1
2
>
>
2.函数y=kx+1的图象如图所示,则 k____0
x
y
1
0
<
y = kx + 1
3.在一次函数y=(2m+2)x+5中,y随着x的增大而减小,
则m是( )
(A). M<-1 ( B). M>-1 (C). M=1 (D). M<1
A
一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直
线。
(0,b)
x
y
o
y=2x+1
x
y
o
y=2x
x
y
o
y=2x
y=2x-1
直线y=2x+1是由直线y=2x向上平移 个单位得。
直线y=2x-1是由直线y=2x向下平移 个单位得到。
1
1
直线y=2x-3是由直线y=2x向 平移 个单位得到。
下
3
b叫做直线y=kx+b(k≠0)在y轴上的截距。
(0,b)
x
y
o
y=kx(k≠0)
(0,b)
x
y
o
(0,b)
直线
与x轴交点
与y轴交点
y=x+1
y=3x+1
y=-2x-1
y=-3-2x
(0,1)
(0,1)
(0,-1)
(0,-3)
(-3/2,0)
( -1/3,0)
(-1,0)
( -1/2,0)
选取适当两点作图:
(1,k+b)
x
y
o
(1)对于函数y=-2x+5,当-1
1
7
2x1+7
2x2+7
(3)已知y是关于x的一次 函数,这个函数的图象经过
A(0,-8),B(1,2)两点,求当1
数形结合训练:
1、已知一次函数y=kx+b(k≠0)平行于
直线y=3x,且过点(1,4),求函数解析式。
2、已知一次函数y=kx+b(k≠0)在y轴上
的截距是-2,且过点(1,3),求函数解析式。
函数解析式为:y=3x+1
函数解析式为:y=5x-2
3、看图象,确定一次函数y=kx+b(k≠0)
中k,b的符号。
o
x
y
o
x
y
o
x
y
k<0
b<0
k>0
b>0
k<0
b=0
4、已知一次函数y=kx+b(k≠0)中
①k>0,b<0 ②k<0,b>0,试作草图。
o
y
x
o
y
x
利用函数图象解一次函数应用题
一、热身练习
1、已知一次函数图象过点(1,2),(2,3)
求这个一次函数解析式;
2、如图,折线ABCDE描述汽车在某一直线公路上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
其中正确的说法共有( )
A、1个 B、2个 C、3个 D、0个
×
√
×
A
温馨提示:
仔细观察图象,
捕捉有效信息!
你还有什么说法?
0
1
2
销售(万件)
800
1300
收入(元)
3、志成公司营销人员的个人收入与每月的销售业绩满足一次函数关系,图象如图所示,由图中的信息可知:营销人员没有销售业绩时的收入是______元。
300
决定一、三象限
k
决定二、四象限
b
决定二、四象限
k
决定一、三象限
b
当k>0时
o
x
y
o
y
x
o
y
x
y
o
x
当k<0时
1、一次函数y=kx+b(k≠0)的图象是经过点(0,b)且平行于直线y=kx (k≠0)的一条直线。
4、选取适当两点作图:
(1,k+b)
2、
3、
中考范例
(哈尔滨)如图,表示一轮船和一快艇沿相同路线,从甲港
到乙港行驶过程中路程随时间变化的图象,解答下列问题:
(1)分别求出表示轮船和快艇行驶过程的函数解析式;
(2)轮船和快艇在途中行驶速度分别是多少
(3) 快艇出发多长时间赶上轮船
解:(1)设轮船行驶过程的函数解析式为y=kx, 由图象知:当x=8时,y=160.
∴8k=160, 解得k=20.
∴轮船行驶过程的函数解析式为y=20x.
设快艇行驶过程的函数解析式为 y=kx+b.
由图象知:当x=2时,y=0; 当x=6时,y=160. 解得k=40,b=-80 ∴快艇行驶过程的函数解析式为y=40x-80.
(2)由图象知,
轮船在8h内行驶160km,
快艇在4h内行驶160km,
轮船行驶速度为20(km/h),
快艇行驶速度为40(km/h)
(3)设轮船出发x小时被快艇赶上。
20x=40x-80,x=4,
∴x-2=4-2=2.
答:快艇出发2小时赶上轮船.
y
x
你还可以设计哪些问题?
1、由于经济和社会发展迅速,用电矛盾越来越突出,为缓
解用电紧张,电力公司制定了新的用电收费标准,每月用
电量x(度)与应付电费y(元)的关系如图所示。
⑴请你根据图像所描述的信息,分别求0≤x≤50和x>50时,
y与x函数关系式。
⑵根据你的分析:
当每月用电量不超过50度时,
收费标准是________;
当每月的用电量超过50度时,
收费标准是______________
_______________________
____________.
当堂练习
y=0.5x (0≤x≤50) ;
=0.9x-20 (x>50).
0.5元/度
不超过50度部分
按0.5元/度计算,超过部分
按0.9元/度计算
2、某单位急需用车,准备和个体车主或租车公司签订月租车合同,设汽车每月行驶x千米,付个体车主的月费用y1元,出租公司的月租费是y2元,图象如图,观察图象回答:
(1)每月行驶的路程
在什么范围内时,
租公司的车合算?
(2)每月行驶的路程
等于多少时,租两家
的费用相同?
(3)如果这个单位估
计每月行驶的路程为
2300千米,那么租哪
一家的车合算?
观察函数图象,并根据你所获得的信息回答问题:
1、折线CAB表示某个实际问题的函数图象,请你编写一道符合该图象意义的应用题;
2、根据你所给出的应用题分别指出x轴、y轴所表示的意义,并写出C、A、B的坐标;
3、求图象AB的函数解析式,注明自变量x取值范围。
y
x
O
A
B
合作编题
C
数与形,相倚依,焉能分作两边飞?
数缺形时少直观,形少数时难入微,
数形结合百般好,隔裂分家万事非,
切莫忘,几何代数统一体,
永远联系、切莫分离!
——我国著名的数学家华罗庚
写一篇与“数形结合”有关的数学小论文,交流展览。
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
