青岛版八年级数学下册10.6一次函数的应用 教学课件(共24张PPT)
文档属性
| 名称 | 青岛版八年级数学下册10.6一次函数的应用 教学课件(共24张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 14:31:49 | ||
图片预览







文档简介
(共24张PPT)
10.6 一次函数的应用
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
1.综合运用一次函数及一元一次不等式,解决简单的实际问题,感悟数形结合、转化和数学建模等数学思想,增强应用意识,提高分析问题和解决问题的能力.
2.分析具体问题,进一步理解函数概念.
1.什么是一次函数
2.一次函数的图象是什么?
3.一次函数具有什么性质?
一般地,我们把形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数,其中x是自变量.
一条直线
k>0,y随着x的增大而增大;
k<0, y随着x的增大而减小.
4.三种函数表示法分别有什么作作用?
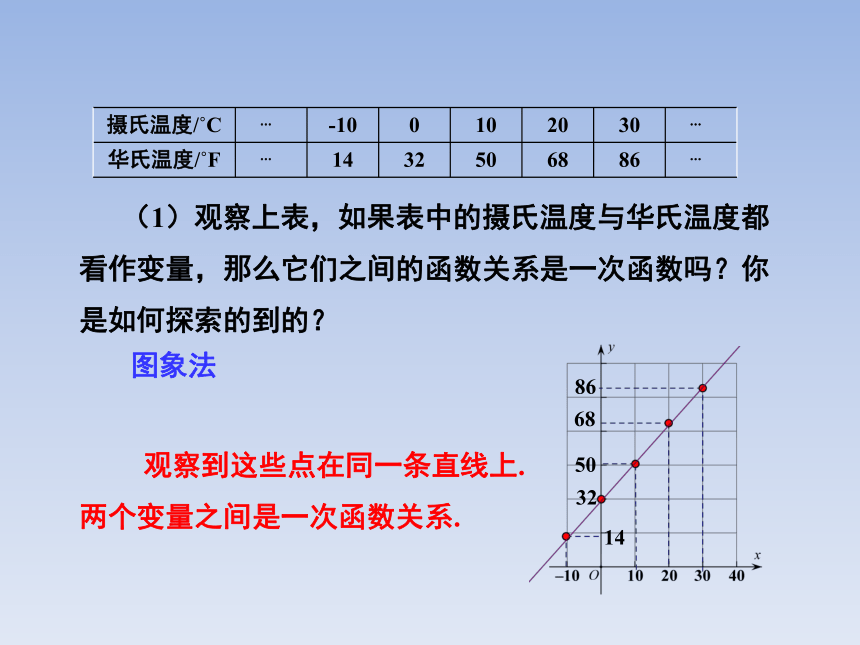
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
(1)观察上表,如果表中的摄氏温度与华氏温度都看作变量,那么它们之间的函数关系是一次函数吗?你是如何探索的到的?
图象法
32
50
68
86
14
观察到这些点在同一条直线上.两个变量之间是一次函数关系.
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
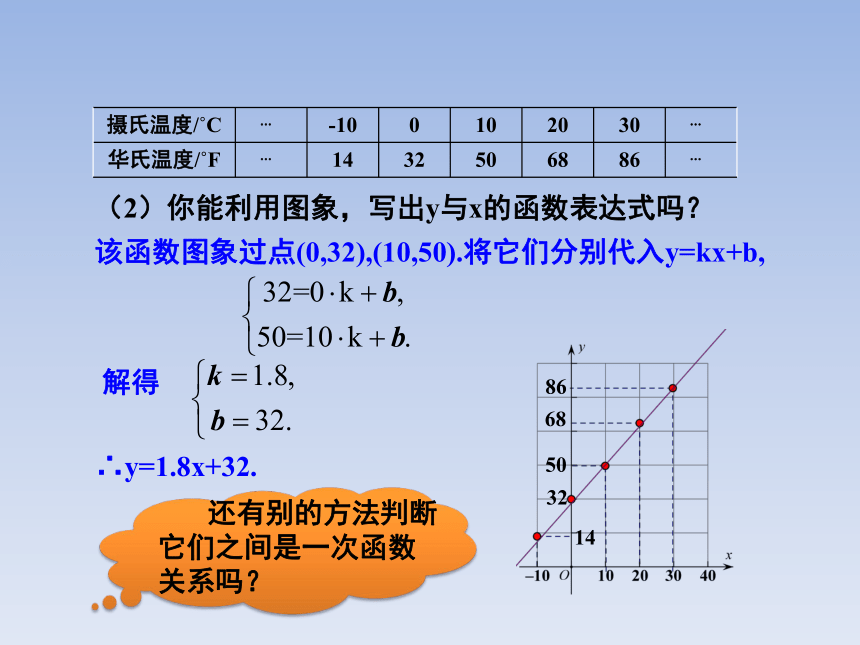
(2)你能利用图象,写出y与x的函数表达式吗?
32
50
68
86
14
该函数图象过点(0,32),(10,50).将它们分别代入y=kx+b,
解得
∴y=1.8x+32.
还有别的方法判断它们之间是一次函数关系吗?
通过观察上表,可以任意发现两个变量对应数值之差的比是一个常数,如 , ,
特别地.如果固 定(0,32)这对值,同样有 ,
, .设摄氏温度为x,相应的华氏温度为y,则有 ,整理得y=1.8x+32,因此y是x的一次函数.
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
(3)你能求出华氏温度为0度(即0 F )时,摄氏温度是多少度?
当y=0时,0=1.8x+32,解得x= ,所以华氏
温度为0 F 时,摄氏温度是 C.
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?你会用哪几种方法解决这个问题?与同学交流.
32
50
68
86
14
例1
山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,一种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少注?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
解:(1)设购买甲种树苗x株,乙种树苗y株,根据题意,得
解得
经检验,方程组的解符合题意.所以购买甲种树苗500株,乙种树苗300株.
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少注?
(2)设购买甲种树苗z株,乙种树苗(800-z)株,由题意得
0.85z+0.9×(800-z)≥0.88×800,
解得 z≤320.
所以甲种树苗至多购买320株.
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
(3)设购买甲种树苗t株,购买树苗的费用为w元,由题意得
w=24t+30×(800-t)==-6t+24000,
所以w是t的一次函数,且由于k=-6<0,因此w随t增大而减小.由(2)知t≤320,因此,当t最大即t=320时,w最小.这是800-320=480,w=-6×320+24000=22080.
所以购买甲种树苗320株、乙种树苗480株,费用最低,最低费用为22080元.
如何利用一次函数解决实际问题
①从现实生活抽象出数学问题,并建立函数表达式;
②根据函数表达式根据函数性质解决问题.
例.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始每袋优惠5%。
(1)写出购买这种化肥的总金额M(元)与购进袋数n的函数表达式,并指出它的自变量的取值范围;
(2)为了快速得到购买这种化肥的总金额,请你利用这个函数的表达式制作一个购买1—10袋化肥总金额的对照表。
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
分析
解:(1)根据题意,可以知道:
当0≤n≤3时,可得函数的表达式为
M=80n.
自变量n的取值范围是0≤n≤3(n是整数)。
当n≥4时,可得函数的表达式为
M=80×3+80×(1-5%)(n-3).
整理,得n≥4时
M=76n+12.
自变量n的取值范围是n≥4(n是整数)。
(2)当n依次取1-10时,分别计算出函数的值,得出下表:
n/袋 1 2 3 4 5 6 7 8 9 10
M/元 80 160 240 316 392 468 544 620 696 772
利用一次函数解决实际问题的步骤是什么
③通过图象准确地读取信息作出判断.
①列解析式并确定函数的定义域;
②根据解析式画图象;
1.如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______。
2.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元,若每月租碟数量为x张. 设零星租碟方式应付金额y1(元), 会员卡租碟方式应付金额y2(元)。
请你制作一张“月租碟费用”的函数图象,帮助来这家店租碟的人判断选取那种租碟方式更合算。
3.甲、乙两个通信公司分别制定了一种移动电话的收费办法。甲公司规定:每月收取月租费50元,每通话一分钟收费0.4元;乙公司规定:不收取月租费,每通话一分钟收费0.6元(通话不到一分钟按一分钟收费).设按照甲、乙两个通信公司的收费标准,通话t分钟的话费分别为y1元和y2元。
怎样选择更节省话费呢
1. 利用一次函数解决实际问题的步骤是什么
2.我们应用了那些数学思想方法?
转化思想
③通过图象准确地读取信息作出判断.
①列解析式并确定函数的定义域;
数形结合的思想
②根据解析式画图象;
作业布置
课本157页 习题10.6第2、3题
10.6 一次函数的应用
Contents
目录
01
02
03
04
旧知回顾
学习目标
新知探究
随堂练习
05
课堂小结
1.综合运用一次函数及一元一次不等式,解决简单的实际问题,感悟数形结合、转化和数学建模等数学思想,增强应用意识,提高分析问题和解决问题的能力.
2.分析具体问题,进一步理解函数概念.
1.什么是一次函数
2.一次函数的图象是什么?
3.一次函数具有什么性质?
一般地,我们把形如y=kx+b(k,b为常数,且k≠0)
的函数叫做一次函数,其中x是自变量.
一条直线
k>0,y随着x的增大而增大;
k<0, y随着x的增大而减小.
4.三种函数表示法分别有什么作作用?
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
(1)观察上表,如果表中的摄氏温度与华氏温度都看作变量,那么它们之间的函数关系是一次函数吗?你是如何探索的到的?
图象法
32
50
68
86
14
观察到这些点在同一条直线上.两个变量之间是一次函数关系.
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
(2)你能利用图象,写出y与x的函数表达式吗?
32
50
68
86
14
该函数图象过点(0,32),(10,50).将它们分别代入y=kx+b,
解得
∴y=1.8x+32.
还有别的方法判断它们之间是一次函数关系吗?
通过观察上表,可以任意发现两个变量对应数值之差的比是一个常数,如 , ,
特别地.如果固 定(0,32)这对值,同样有 ,
, .设摄氏温度为x,相应的华氏温度为y,则有 ,整理得y=1.8x+32,因此y是x的一次函数.
摄氏温度/ C -10 0 10 20 30
华氏温度/ F 14 32 50 68 86
(3)你能求出华氏温度为0度(即0 F )时,摄氏温度是多少度?
当y=0时,0=1.8x+32,解得x= ,所以华氏
温度为0 F 时,摄氏温度是 C.
(4)华氏温度的值与对应的摄氏温度的值有相等的可能吗?你会用哪几种方法解决这个问题?与同学交流.
32
50
68
86
14
例1
山青林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,一种树苗每株30元.根据相关资料,甲、乙两种树苗的成活率分别是85%,90%.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少注?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
(1)如果购买这两种树苗共用去21000元,甲、乙两种树苗各买了多少株?
解:(1)设购买甲种树苗x株,乙种树苗y株,根据题意,得
解得
经检验,方程组的解符合题意.所以购买甲种树苗500株,乙种树苗300株.
(2)如果为了保证这批树苗的总成活率不低于88%,甲种树苗至多购买多少注?
(2)设购买甲种树苗z株,乙种树苗(800-z)株,由题意得
0.85z+0.9×(800-z)≥0.88×800,
解得 z≤320.
所以甲种树苗至多购买320株.
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求最低费用.
(3)设购买甲种树苗t株,购买树苗的费用为w元,由题意得
w=24t+30×(800-t)==-6t+24000,
所以w是t的一次函数,且由于k=-6<0,因此w随t增大而减小.由(2)知t≤320,因此,当t最大即t=320时,w最小.这是800-320=480,w=-6×320+24000=22080.
所以购买甲种树苗320株、乙种树苗480株,费用最低,最低费用为22080元.
如何利用一次函数解决实际问题
①从现实生活抽象出数学问题,并建立函数表达式;
②根据函数表达式根据函数性质解决问题.
例.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始每袋优惠5%。
(1)写出购买这种化肥的总金额M(元)与购进袋数n的函数表达式,并指出它的自变量的取值范围;
(2)为了快速得到购买这种化肥的总金额,请你利用这个函数的表达式制作一个购买1—10袋化肥总金额的对照表。
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
分析
解:(1)根据题意,可以知道:
当0≤n≤3时,可得函数的表达式为
M=80n.
自变量n的取值范围是0≤n≤3(n是整数)。
当n≥4时,可得函数的表达式为
M=80×3+80×(1-5%)(n-3).
整理,得n≥4时
M=76n+12.
自变量n的取值范围是n≥4(n是整数)。
(2)当n依次取1-10时,分别计算出函数的值,得出下表:
n/袋 1 2 3 4 5 6 7 8 9 10
M/元 80 160 240 316 392 468 544 620 696 772
利用一次函数解决实际问题的步骤是什么
③通过图象准确地读取信息作出判断.
①列解析式并确定函数的定义域;
②根据解析式画图象;
1.如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______。
2.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元,若每月租碟数量为x张. 设零星租碟方式应付金额y1(元), 会员卡租碟方式应付金额y2(元)。
请你制作一张“月租碟费用”的函数图象,帮助来这家店租碟的人判断选取那种租碟方式更合算。
3.甲、乙两个通信公司分别制定了一种移动电话的收费办法。甲公司规定:每月收取月租费50元,每通话一分钟收费0.4元;乙公司规定:不收取月租费,每通话一分钟收费0.6元(通话不到一分钟按一分钟收费).设按照甲、乙两个通信公司的收费标准,通话t分钟的话费分别为y1元和y2元。
怎样选择更节省话费呢
1. 利用一次函数解决实际问题的步骤是什么
2.我们应用了那些数学思想方法?
转化思想
③通过图象准确地读取信息作出判断.
①列解析式并确定函数的定义域;
数形结合的思想
②根据解析式画图象;
作业布置
课本157页 习题10.6第2、3题
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
