青岛版八年级数学下册11.2图形的旋转 教学课件(共16张PPT)
文档属性
| 名称 | 青岛版八年级数学下册11.2图形的旋转 教学课件(共16张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 14:46:20 | ||
图片预览






文档简介
(共16张PPT)
第11章 图形的平移与旋转
11.2 图形的旋转(2)
Contents
目录
01
02
03
04
旧知回顾
学习目标
例题讲解
随堂练习
1.通过例题感受图形的旋转的性质.
2.会利用平移的性质解决旋转问题.
◆什么叫图形的旋转?
在平面内,将一个图形绕 沿 或___________转动 ,图形的这种变化叫做旋转。
一个定点
一个角度
逆时针方向
顺时针
◆旋转的三要素是什么?
旋转中心
旋转方向
旋转角
◆图形的旋转的性质是什么?
(1)一个图形和它经过旋转所得到的图象中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角都是旋转角.
(2)旋转只改变图形的位置,不改变图形的形状和大小.
C
D
O
A
B
A
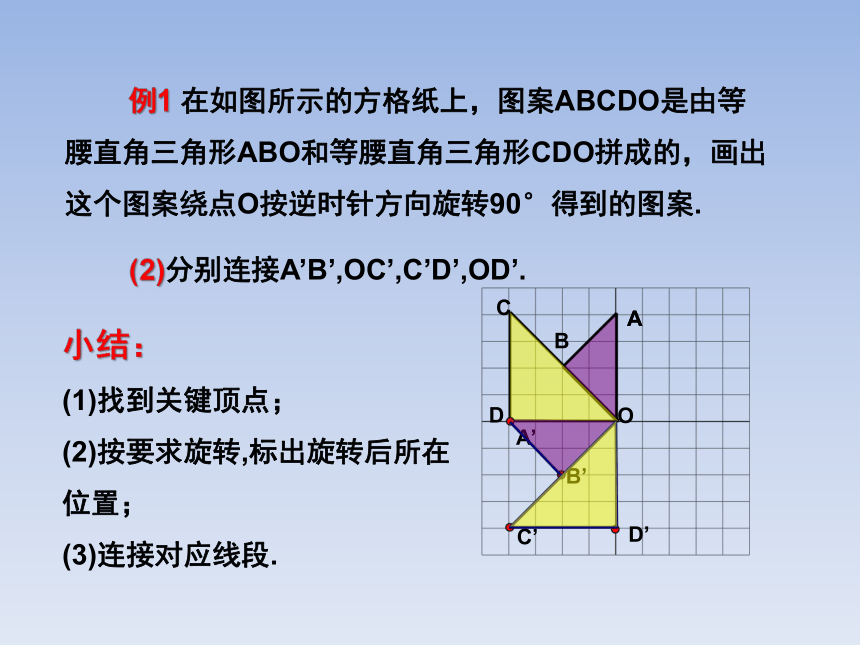
例1 在如图所示的方格纸上,图案ABCDO是由等腰直角三角形ABO和等腰直角三角形CDO拼成的,画出这个图案绕点O按逆时针方向旋转90°得到的图案.
例1 (1)设方格纸上每个小正方形的边长为1个单位长度.点A,B,C,D绕点O按逆时针旋转90°得到的点分别记作A’,B’,C’,D’,位置如图所示. A’与点D重合.
B’
C’
D’
A’
(2)分别连接A’B’,OC’,C’D’,OD’.
例1 在如图所示的方格纸上,图案ABCDO是由等腰直角三角形ABO和等腰直角三角形CDO拼成的,画出这个图案绕点O按逆时针方向旋转90°得到的图案.
C
D
O
A
B
B’
C’
D’
A
A’
小结:
(1)找到关键顶点;
(2)按要求旋转,标出旋转后所在位置;
(3)连接对应线段.
例2 如图,点E是正方形ABCD的边CD上 一点,将△ADE绕点A按顺时针方向旋转一定的角度,使点E落到CB的延长线上的点F处.
(1)写出它的旋转角; (2)若EF=4,求AE的长.
解(1)旋转中心是点A,当AE旋转AF时,点E的对应点是点F,
设点D的对应点是点D’,由旋转的基本性质:AD=AD’=AB,∠FAD’=∠EAD,所以点D’与点B重合.
∵ ∠BAD=90°,
∴ 旋转角是90°.
(2)∵A是旋转中心,E与F,D与B是对应点,根据旋转的基本性质,
∴AF=AE,∠FAE=∠BAD=90°.
∴△AFE是等腰直角三角形.
∴AF2+AE2=EF2.
∵EF=4,
∴2AE2=42
∴AE=
1.如图,△ABC是等边三角形,点P是△ABC内一点.△APC沿逆时针方向旋转后与△AP′B重合,则旋转中心是______,最小旋转角等于______度.
解:根据旋转的性质可知,△APC沿逆时针方向旋转后与△AP′B重合, 则旋转中心是A, 最小旋转角等于360°-60°=300°.
A
300
2.如图,E是正方形ABCD中CD边上一点.把△ADE绕点A顺时针旋转90°后得到△ABF,G是BC边上一点,且∠EAG=45°,连接GE. (1)观察△AFG和△AEG,你发现△AFG和△AEG有什么关系?请说明理由. (2)若AB=1,EG= ,求△CEG的周长和面积.
解:(1)连接EF. ∵△ABF是△ADE绕点A顺时针旋转90°后得到的, ∴AE=AF,DE=BF,∠DAE=∠BAF, 又∵∠EAG=45°, ∴∠DAE+∠BAG=45°,∴∠BAF+∠BAG=∠FAG=45°, ∴∠EAG=∠FAG. 在△AEF中,AE=AF,∠EAG=∠FAG, ∴AG垂直平分EF,即点E、F是关于AG的对称点. ∴△AFG和△AEG是关于直线AG的轴对称图形.
(2)∵△AFG和△AEG是关于直线AG的轴对称图形. ∴△AFG≌△AEG, ∴FG=EG.
∴C△CEG=EG+GC+EC=FG+GC+EC=
=BC+CD=1+1=2.
∵△ABF≌△ADE,△AFG≌△AEG,
∴ S正方形ABCD=2S△AFG+ S△GCE.
∵S△AFG= FG AB= EG AB= × ×1= ,
∴S△CEG=S正方形ABCD -2S△AFG=1-2× = .
3.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E. (1)说明△ADC ≌ △CEB; (2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.
图1
图2
解:(1)∵直线MN经过点C,∠ACB=90°, ∴∠ACD+∠BCE=90°, 又AD⊥MN, ∴∠ACD+∠DAC=90°, ∴∠DAC=∠BCE. ∵BE⊥MN, ∴∠ADC=∠CEB=90°, 在△ADC和△CEB中, ∠DAC=∠ECB,AC=BC,∠ADC=∠CEB, ∴△ADC≌△CEB(AAS).
图1
(2)AD=DE+BE. 理由:由旋转的性质可得:CD=BE,AD=CE, ∴AD=CE=CD+DE=BE+DE.
图2
第11章 图形的平移与旋转
11.2 图形的旋转(2)
Contents
目录
01
02
03
04
旧知回顾
学习目标
例题讲解
随堂练习
1.通过例题感受图形的旋转的性质.
2.会利用平移的性质解决旋转问题.
◆什么叫图形的旋转?
在平面内,将一个图形绕 沿 或___________转动 ,图形的这种变化叫做旋转。
一个定点
一个角度
逆时针方向
顺时针
◆旋转的三要素是什么?
旋转中心
旋转方向
旋转角
◆图形的旋转的性质是什么?
(1)一个图形和它经过旋转所得到的图象中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心的连线所成的角都是旋转角.
(2)旋转只改变图形的位置,不改变图形的形状和大小.
C
D
O
A
B
A
例1 在如图所示的方格纸上,图案ABCDO是由等腰直角三角形ABO和等腰直角三角形CDO拼成的,画出这个图案绕点O按逆时针方向旋转90°得到的图案.
例1 (1)设方格纸上每个小正方形的边长为1个单位长度.点A,B,C,D绕点O按逆时针旋转90°得到的点分别记作A’,B’,C’,D’,位置如图所示. A’与点D重合.
B’
C’
D’
A’
(2)分别连接A’B’,OC’,C’D’,OD’.
例1 在如图所示的方格纸上,图案ABCDO是由等腰直角三角形ABO和等腰直角三角形CDO拼成的,画出这个图案绕点O按逆时针方向旋转90°得到的图案.
C
D
O
A
B
B’
C’
D’
A
A’
小结:
(1)找到关键顶点;
(2)按要求旋转,标出旋转后所在位置;
(3)连接对应线段.
例2 如图,点E是正方形ABCD的边CD上 一点,将△ADE绕点A按顺时针方向旋转一定的角度,使点E落到CB的延长线上的点F处.
(1)写出它的旋转角; (2)若EF=4,求AE的长.
解(1)旋转中心是点A,当AE旋转AF时,点E的对应点是点F,
设点D的对应点是点D’,由旋转的基本性质:AD=AD’=AB,∠FAD’=∠EAD,所以点D’与点B重合.
∵ ∠BAD=90°,
∴ 旋转角是90°.
(2)∵A是旋转中心,E与F,D与B是对应点,根据旋转的基本性质,
∴AF=AE,∠FAE=∠BAD=90°.
∴△AFE是等腰直角三角形.
∴AF2+AE2=EF2.
∵EF=4,
∴2AE2=42
∴AE=
1.如图,△ABC是等边三角形,点P是△ABC内一点.△APC沿逆时针方向旋转后与△AP′B重合,则旋转中心是______,最小旋转角等于______度.
解:根据旋转的性质可知,△APC沿逆时针方向旋转后与△AP′B重合, 则旋转中心是A, 最小旋转角等于360°-60°=300°.
A
300
2.如图,E是正方形ABCD中CD边上一点.把△ADE绕点A顺时针旋转90°后得到△ABF,G是BC边上一点,且∠EAG=45°,连接GE. (1)观察△AFG和△AEG,你发现△AFG和△AEG有什么关系?请说明理由. (2)若AB=1,EG= ,求△CEG的周长和面积.
解:(1)连接EF. ∵△ABF是△ADE绕点A顺时针旋转90°后得到的, ∴AE=AF,DE=BF,∠DAE=∠BAF, 又∵∠EAG=45°, ∴∠DAE+∠BAG=45°,∴∠BAF+∠BAG=∠FAG=45°, ∴∠EAG=∠FAG. 在△AEF中,AE=AF,∠EAG=∠FAG, ∴AG垂直平分EF,即点E、F是关于AG的对称点. ∴△AFG和△AEG是关于直线AG的轴对称图形.
(2)∵△AFG和△AEG是关于直线AG的轴对称图形. ∴△AFG≌△AEG, ∴FG=EG.
∴C△CEG=EG+GC+EC=FG+GC+EC=
=BC+CD=1+1=2.
∵△ABF≌△ADE,△AFG≌△AEG,
∴ S正方形ABCD=2S△AFG+ S△GCE.
∵S△AFG= FG AB= EG AB= × ×1= ,
∴S△CEG=S正方形ABCD -2S△AFG=1-2× = .
3.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E. (1)说明△ADC ≌ △CEB; (2)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.
图1
图2
解:(1)∵直线MN经过点C,∠ACB=90°, ∴∠ACD+∠BCE=90°, 又AD⊥MN, ∴∠ACD+∠DAC=90°, ∴∠DAC=∠BCE. ∵BE⊥MN, ∴∠ADC=∠CEB=90°, 在△ADC和△CEB中, ∠DAC=∠ECB,AC=BC,∠ADC=∠CEB, ∴△ADC≌△CEB(AAS).
图1
(2)AD=DE+BE. 理由:由旋转的性质可得:CD=BE,AD=CE, ∴AD=CE=CD+DE=BE+DE.
图2
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
