青岛版八年级数学下册期末 复习课件 (共74张PPT)
文档属性
| 名称 | 青岛版八年级数学下册期末 复习课件 (共74张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 15:03:45 | ||
图片预览








文档简介
(共74张PPT)
期末复习
第六章 平行四边形
四 边 形
平行四边形
一 般 四 边 形
一般的平行四边形
特 殊 的平行四边形
菱 形
矩 形
正方形
三角形的中位线及其定理
平 行 四 边 形
性质
文字语言叙述
几何符号表述
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
在 ABCD中
∴四边形ABCD是 ABCD
A
B
C
D
O
AB=CDAD=BC AB∥CDAD∥BC
∠A=∠C, ∠B=∠D ∠A+∠B=1800
OA=OC
OB=OD
判别
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
∵在四边形ABCD中
矩 形
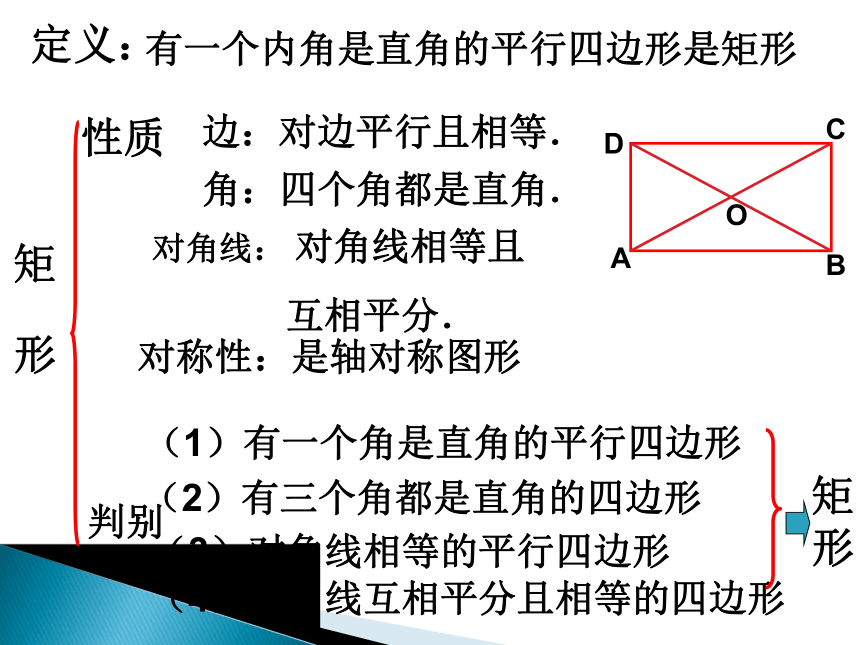
定义:
有一个内角是直角的平行四边形是矩形
性质
对称性:是轴对称图形
判别
(2)有三个角都是直角的四边形
(4)对角线互相平分且相等的四边形
(1)有一个角是直角的平行四边形
(3)对角线相等的平行四边形
矩形
A
B
C
D
O
边:对边平行且相等.
对角线: 对角线相等且
互相平分.
角:四个角都是直角.
菱 形
定义:有一组邻边相等的平行四边形是菱形
性质
判别
⑴有一组邻边相等的平行四边形
⑵四条边都相等的四边形
⑶对角线互相垂直平分的四边形
⑷对角线互相垂直的平行四边形
菱形
A
B
C
D
O
边:四条边都相等,对边平行.
对角线: 对角线互相垂直平分.
对称性:即是轴对称图形,
又是中心对称图形.
角:对角相等,邻角互补.
正 方 形
定义:一组邻边相等且有一个角是直角的四边形叫正方形
性质
判别
⑴先判定四边形是矩形;再判定这个矩形是菱形
⑵先判定四边形是菱形;再判定这个菱形是矩形
A
B
C
D
O
对称性:即是轴对称图形又是中心对称图形.
边:四条边都相等,对边平行.
对角线: 对角线相等且互相垂直平分.
角:四个角都是直角.
三角形的中位线的性质:
三角形的中位线平行于第三边,
并且等于它的一半。
数学语言:
∵在△ABC中,D 、E分别
是AB 、AC的中点.
∴ DE∥BC, DE= BC
2
1
A
B
C
D
E
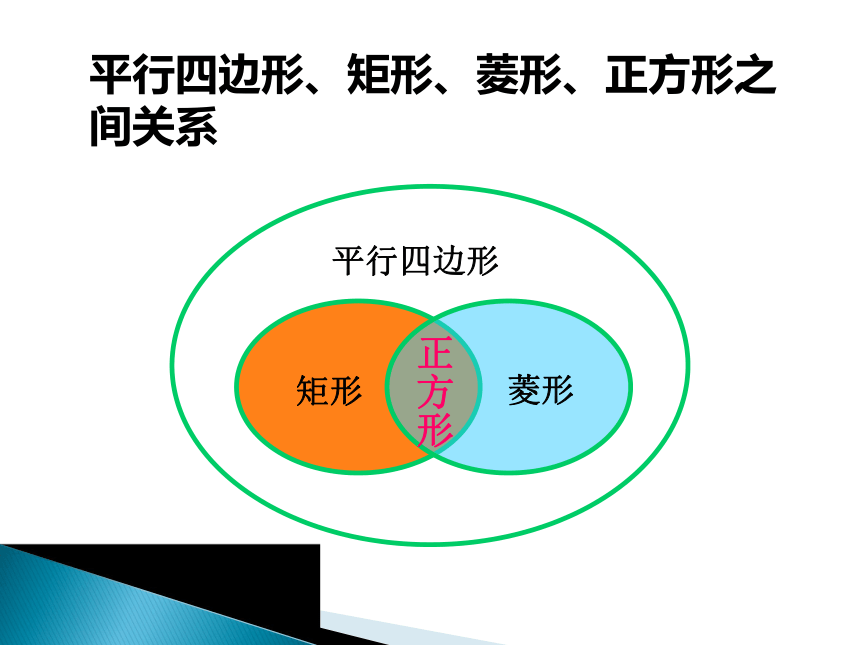
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
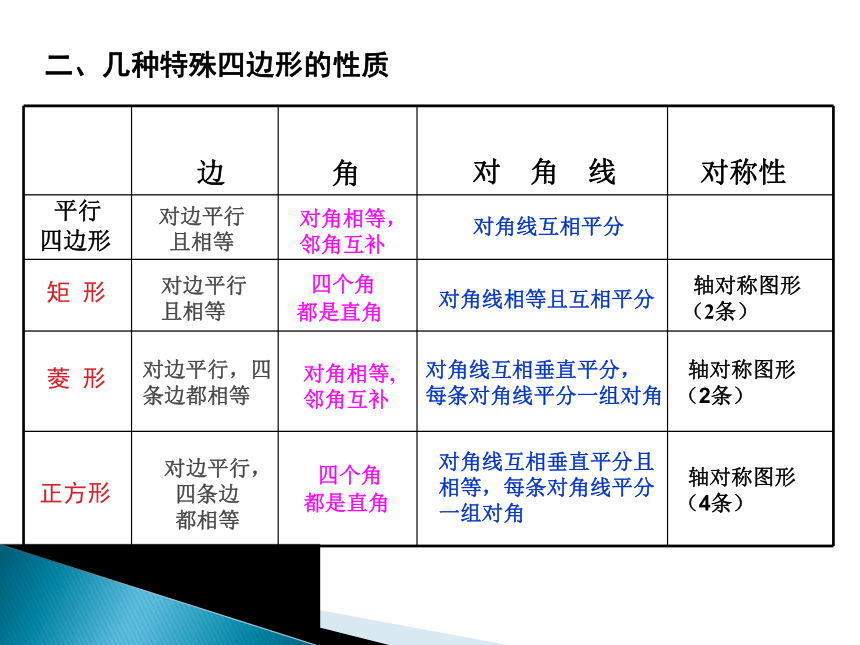
二、几种特殊四边形的性质
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等且互相平分
对角线互相垂直平分,
每条对角线平分一组对角
对角线互相垂直平分且
相等,每条对角线平分
一组对角
对称性
轴对称图形
(2条)
轴对称图形
(2条)
轴对称图形
(4条)
三、特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)两组对角
(4)对角线互相平分;
(5)一组对边平行且相等
矩 形
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
分别相等;
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
巩固练习
(一)判断题:
1.平行四边形的对角线相等; ( )
2.矩形的四个角都相等; ( )
3.菱形的对角线互相垂直平分; ( )
4.有一个角是直角且邻边相等的平行四边形是正方形; ( )
5.一组对边平行且相等的四边形是平行四边形; ( )
6.对角线相等的四边形是矩形; ( )
(二)选择题:
D
2.正方形具有而菱形不一定具有的性质是( )
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角 (D)对角线互相垂直。
B
3.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形 (B)正方形 (C ) 菱形 (D)平行四边形
D
4.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形
B
5.下列性质中,平行四边形不一定具备的是( )
(A)对角相等 (B)邻角互补 (C )对角互补 (D)内角和是360°
C
(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;
1.下面判定四边形是平行四边形的方法中,错误的是( )
(C)一组对边相等,另一组对边也相等;
(D)一组对边平行,另一组对边相等
6.能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等。 (B)两条对角线互相平分
(C )两条对角线互相垂直 (D)一对邻角的和为180°
B
7.不能判定四边形ABCD是平行四边形的条件是( )
//
(A) AB =CD, AD =BC (B) BC AD
(C) AB//DC, AD//BC (D) AB =CD,AD//BC
D
第七章 实数
1.了解无理数与实数的概念,学会区分无理数与有理数,会对实数进行分类.
2.了解算术平方根,平方根,立方根的概念,会用根号表示数的平方根立方根,掌握三者的区别.
3.掌握勾股定理及其逆定理的内容.会用勾股定理解决实际问题,会用逆定理判定直角三角形(难点).
算术平方根
负的平方根
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
不要遗漏
2.解方程:
当方程中出现平方时,若有解,一般都有两个解
解:
3.
位置如图所示,
试化简
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
勾股定理 逆定理
两直角边的平方和等于斜边的平方即
若三角形的三边满足
则三角形是直角三角形
是直角三角形的性质
用来判定三角形是否是直角三角形
内容
用途
勾股定理与逆定理
2、直角三角形两条直角边的长为
1和 ,求斜边上的高。
1、三角形三边 a,b,c满足
则此三角形为________________.
等腰直角三角形
在Rt⊿ABC其中两边 a,b满足
则此三角形c边长为________________.
不等号的两边都是整式,而且只有一个未知数,未知数的最高次数是一次
数轴、定点、定方向
用不等号连接而成的数学式子叫做不等式
1、不等号:
表示不等关系的符号称为不等号。一般包括“>”、“<”、“≥”、“≤”、“≠”五种,其意义、读法如下表所示:
名称 符号 读法 意义 例子
大于号
>
大于
左边的量大于右边的量
3>2
小于号
<
小于
左边的量小于右边的量
-5<1
大于或等于号
1.大于或等于
2.不小于
左边的量不小于右边的量
a≥4
≤
≥
≠
小于或等于号
1.小于或等于
2.不大于
左边的量不大于右边的量
不等号
不等于
左右两边的量不相等
b≤-1
c≠0
例:用不等号表示下列两数或两式的关系:
(1)3____-1;(2)-10____0;(3)2x2_____0;(4)|2x|______|-3x|.
>
<
≥
≤
3.不等到式的基本性质:
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
性质 3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
注:在不等式两边都乘以(或除以)同一个整式时,应考虑整式为正数、负数、零三种情况。
4、不等式的解:
使不等式成立的未知数的值.
5、不等式的解集:
一个含有未知数的不等式的所有解,组成了这个不等式的解集。
6、解不等式:
求不等式解集的过程
其实质就是把不等式化为“x>a或x≥a或x7、用数轴表示不等式的解集:
大于向右画,小于向左画.
a
x>a
a
xa
x≥a
a
x≤a
8、不等式解集中最值问题:
对于不等式x≥a的解集有最小值,最小值为x=a;对于不等式x≤a的解集有最大值,最大值为x=a,而不等式x>a的解集没有最小值,x例:x≥2时x的最小值是a,x≤5时x的最大值是b,试求ba的值。
解:根据已知条件,得a=2,b=5则ba=52=25
9、一元一次不等式:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
解一元一次不等式和解一元一次方程类似,有
去分母 去括号 移项 合并同类项
系数化为1等步骤.
与一元一次方程解法区别在哪里
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
10、一元一次不等式的解法
求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
11、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
12、一元一次不等式组的解集:
一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
13、一元一次不等式组的解集的取法:
最简不等式组(ax>a
x>b
xxx>a
xxx>b
a
b
a
b
a
b
a
b
x>b
xa无解
同大取大
同小取小
大小小大取中间
大大小小解不了
14、一元一次不等式组的解法:
步骤:(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点。
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
15、一元一次不等式(组)的应用:
(1)利用不等式解决商家销售中的利润问题:
例:某商店将一件商品的进价提价20%的,再降价30%,以105元出售,问该商店卖出这件产品,是盈利还是亏损?
解:设这件商品的进价为x元,
则x(1+20%)(1-30%)=105,
解得x=125,因为105<125,
所以该商店卖出这件产品亏损了。
(2)利用不等式解决方案设计问题:
例:某校在“五一”期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且有一辆不空也不满。
(1)求外出旅游的学生人数是多少?
(2)已知45座客车座客车每辆租金250元,60座客车每辆租金300元,为了节省租金,并保证每个学生都能有座,决定怎样租用客车,使得租金最少?
解:设单独租用45座的客车x辆,则单独租用了(x-1)辆60座的客车。根据题意得:
0<45x-60(x-2)<60
解得:4所以学生数为:45×5=225人、45×6=270人或45×7=315人。
去分母
去括号
移项
合并同类项
未知数的系数化为1
注意用不等式性质3,即不等式两边乘或
除以一个负数时,改变不等号的方向。
返回
类型(a>b) 解集 数轴显示 语言叙述
两大选取大
两小应选小
大于小小于大中间找
小于小大于大无处挑
a
b
a
b
a
b
a
b
x>a
bx无解
返回
列一元一次不等式组解应用题
的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,明确 各数量之间的关系;
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:列不等式组;
(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
返回
二次根式
性质
运算
概念
二次根式
最简二次根式
同类二次根式
二次根式的概念
形如 (a 0)的式子
叫做二次根式
1.二次根式的定义:
2.二次根式的识别:
(1)被开方数
(2)根指数是2
题型1:确定二次根式中被开方数所含字母的取值范围.
1. 当 X _____时, 有意义。
3.求下列二次根式中字母的取值范围
解得 - 5≤x<3
解:
①
②
说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组)
≤3
a=4
2. +
有意义的条件是
题型2:二次根式的非负性的应用.
1.已知: + =0,求 x-y 的值.
2.已知x,y为实数,且
+3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1
解:由题意,得 x-4=0 且 2x+y=0
解得 x=4,y=-8
x-y=4-(-8)= 4+8 =12
D
注意:几个非负数的和为0,则每一个非负数必为0。
题型3:最简二次根式:
1、被开方数不含分数;
2、被开方数不含开的尽方的因数或因式;
注意:分母中不含二次根式。
化简二次根式的方法:
(1)如果被开方数是整数或整式时,先因数分解或因式分解,然后利用积的算术平方根的性质,将式子化简。
(2)如果被开方数是分数或分式时,先利用商的算术平方根的性质,将其变为二次根式相除的形式,然后利用分母有理化,将式子化简。
题型4:利用
进行分解因式
例:分解因式:
1.回顾并理解掌握正比例函数、一次函数的概念、图象、性质
及解析式的确定,查漏补缺;理解回顾一次函数与一元一次
方程、一元一次不等式、二元一次方程组的关系。会用相关
知识解决实际问题。
2.提升学生自主构建知识体系的能力,进一步提高学生数形结
合思想和用函数思想解决问题的能力。
3.在学习过程中,培养学生独立思考、合作探究的意识和能力,
进一步激发学生学习数学的兴趣。
1.一次函数的图象及性质的归纳和总结.
2.通过一次函数图象深刻认识方程(组)、
不等式(组)的解.
3.运用一次函数的图象及其性质解决有关实际问题.
1.一次函数的实际应用.
2. 函数思想、数形结合的渗透和应用.
变化的
世界
函数
定义
函数关系的表示方法
图象法
列表法
表达式
一
次
函
数
定义
图象
性质
函数与一元一次方程(组)的关系
函数与一元一次不等式的关系
应用
Y=kx+b(k≠0)
直线
对应性
增减性
实际应用
待定系数法
正比例函数
(1)在某一问题中,保持 的量叫常量,可以取 的量,叫做变量.
不变
不同数值
(2)函数:在同一变化过程中,有两个变量x和y,如果对于x的每—个值,y都有______________与之对应,我们就把y叫做x的函数,其中x叫做自变量.如果自变量x取a时,y的值是b,就把b叫做x=a时的函数值.
唯一确定的值
一、知识要点
(3)函数的图象:用图像表示变量之间函数关系的方法叫做图象法
1. 函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k______),那么y叫做x的一次函数。
kx +b
≠0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,
⑵比例系数_____。
1
k≠0
特别地,当b_____时,函数y=____(k____)叫做正比例函数。
= 0
2.一次函数的概念
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
<
<
>
2.一次函数的图象
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大
减小
3.一次函数的性质
(1)增减性
从表中可以看出:由一次函数经过的象限可以判断k、b的符号,
反过来,由k、b的符号也可以判断图象经过的象限.
(2)k.b的符号与图象所在位置对应性
以二元一次方程的解为坐标的点都在对应一次函数的图像上;
以一次函数的图像上点的坐标都是对应二元一次方程的解。
4.一次函数与二元一次方程组的关系(对应性)
. 二元一次方程组的解与以这两个方程
所对应的一次函数图象的交点坐标相对应。
解:把x=1时, y=5;x=6时,y=0分别代入解析式,得
解得
∴此一次函数的解析式为 y= - x+6
用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
例:已知一次函数y=kx+b(k≠0)当x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。
5.一次函数的应用
(1)待定系数法:
一.使用直译法求解一次函数应用题
所谓直译法就是将题中的关键语句“译”成代数式,然后找出函数关系、列出一次函数解析式,从而解决问题的方法。
二.使用列表法求解一次函数应用题
列表法就是将题目中的各个量列成一个表格,从而理顺它们之间的数量关系,以便于从中找到函数关系的解题方法。
三.使用图示法求解一次函数应用题
所谓图示法就是用图形来表示题中的数量关系,从而观察出函数关系的解题方法。
此法对于某些一次函数问题非常有效,解题过程直观明了。
小结
1.一次函数的概念;
2.一次函数的图象;
3.一次函数的性质;
5. 一次函数的与方程、方程组及不等式的关系
4. 一次函数的应用
(1)待定系数法;
(2)利用一次函数解决实际问题。
第十一章
旋转前后的图形完全重合
轴对称图形
中心对称图形
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
3
翻转前后的图形完全重合
E
H
F
G
1、如图,正方形EFGH是由正方形ABCD平移得到的, 则有( )
A.点E和B对应 B. 线段AD和EH对应
C. 线段AC和FH对应 D. ∠B和∠D对应
A
B
C
D
B
平移方向和距离呢?
2、如图△ABC是等腰直角三角形, 点D是斜边BC中点, △ABD绕点A旋转到△ACE的位置, 恰与△ACD组成正方形ADCE, 则△ABD所经过的旋转是( )
B
C
D
E
A
A. 顺时针旋转225° B. 逆时针旋转45°
C. 顺时针旋转315° D. 逆时针旋转90°
D
3、下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
D
4、已知四边形ABCD和点O,画四边形A'B'C'D' 使它与已知四边形关于点O对称。
A
B
C
D
O
A'
B'
C'
D'
画法:
四边形A'B'C'D'就是所求的四边形。
5. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
谈谈你本节课的收获是什么?
期末复习
第六章 平行四边形
四 边 形
平行四边形
一 般 四 边 形
一般的平行四边形
特 殊 的平行四边形
菱 形
矩 形
正方形
三角形的中位线及其定理
平 行 四 边 形
性质
文字语言叙述
几何符号表述
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
在 ABCD中
∴四边形ABCD是 ABCD
A
B
C
D
O
AB=CDAD=BC AB∥CDAD∥BC
∠A=∠C, ∠B=∠D ∠A+∠B=1800
OA=OC
OB=OD
判别
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
∵在四边形ABCD中
矩 形
定义:
有一个内角是直角的平行四边形是矩形
性质
对称性:是轴对称图形
判别
(2)有三个角都是直角的四边形
(4)对角线互相平分且相等的四边形
(1)有一个角是直角的平行四边形
(3)对角线相等的平行四边形
矩形
A
B
C
D
O
边:对边平行且相等.
对角线: 对角线相等且
互相平分.
角:四个角都是直角.
菱 形
定义:有一组邻边相等的平行四边形是菱形
性质
判别
⑴有一组邻边相等的平行四边形
⑵四条边都相等的四边形
⑶对角线互相垂直平分的四边形
⑷对角线互相垂直的平行四边形
菱形
A
B
C
D
O
边:四条边都相等,对边平行.
对角线: 对角线互相垂直平分.
对称性:即是轴对称图形,
又是中心对称图形.
角:对角相等,邻角互补.
正 方 形
定义:一组邻边相等且有一个角是直角的四边形叫正方形
性质
判别
⑴先判定四边形是矩形;再判定这个矩形是菱形
⑵先判定四边形是菱形;再判定这个菱形是矩形
A
B
C
D
O
对称性:即是轴对称图形又是中心对称图形.
边:四条边都相等,对边平行.
对角线: 对角线相等且互相垂直平分.
角:四个角都是直角.
三角形的中位线的性质:
三角形的中位线平行于第三边,
并且等于它的一半。
数学语言:
∵在△ABC中,D 、E分别
是AB 、AC的中点.
∴ DE∥BC, DE= BC
2
1
A
B
C
D
E
平行四边形
矩形
菱形
正方形
平行四边形、矩形、菱形、正方形之间关系
二、几种特殊四边形的性质
平行
四边形
矩 形
菱 形
正方形
边
对边平行
且相等
对边平行
且相等
对边平行,四
条边都相等
对边平行,
四条边
都相等
角
对角相等,
邻角互补
四个角
都是直角
对角相等,
邻角互补
四个角
都是直角
对 角 线
对角线互相平分
对角线相等且互相平分
对角线互相垂直平分,
每条对角线平分一组对角
对角线互相垂直平分且
相等,每条对角线平分
一组对角
对称性
轴对称图形
(2条)
轴对称图形
(2条)
轴对称图形
(4条)
三、特殊四边形的常用判定方法
平行
四边形
(1)两组对边分别平行;
(2)两组对边分别相等;
(3)两组对角
(4)对角线互相平分;
(5)一组对边平行且相等
矩 形
(1)有一个角是直角的平行四边形是矩形;
(2)有三个角是直角的四边形是矩形;
(3)对角线相等的平行四边形是矩形。
菱 形
(1)有一组邻边相等的平行四边形是菱形;
(2)四条边都相等的四边形是菱形;
(3)对角线互相垂直的平行四边形是菱形。
正方形
(2)有一组邻边相等的矩形是正方形;
(3)有一个角是直角的菱形是正方形。
分别相等;
(1)有一个角是直角且有一组邻边相等的平行四边形是正方形;
巩固练习
(一)判断题:
1.平行四边形的对角线相等; ( )
2.矩形的四个角都相等; ( )
3.菱形的对角线互相垂直平分; ( )
4.有一个角是直角且邻边相等的平行四边形是正方形; ( )
5.一组对边平行且相等的四边形是平行四边形; ( )
6.对角线相等的四边形是矩形; ( )
(二)选择题:
D
2.正方形具有而菱形不一定具有的性质是( )
(A)对角线互相平分。 (B)对角线相等。
(C)对角线平分一组对角 (D)对角线互相垂直。
B
3.顺次连结四边形各边中点所得到的四边形一定是( )
(A)矩形 (B)正方形 (C ) 菱形 (D)平行四边形
D
4.内角和等于外角和的多边形是( )
(A) 三角形。(B)四边形。(C )五边形。(D)六边形
B
5.下列性质中,平行四边形不一定具备的是( )
(A)对角相等 (B)邻角互补 (C )对角互补 (D)内角和是360°
C
(A)一组对边平行,另一组对边也平行;
(B)一组对角相等,另一组对角也相等;
1.下面判定四边形是平行四边形的方法中,错误的是( )
(C)一组对边相等,另一组对边也相等;
(D)一组对边平行,另一组对边相等
6.能够判定一个四边形是平行四边形的条件是( )
(A)一组对角相等。 (B)两条对角线互相平分
(C )两条对角线互相垂直 (D)一对邻角的和为180°
B
7.不能判定四边形ABCD是平行四边形的条件是( )
//
(A) AB =CD, AD =BC (B) BC AD
(C) AB//DC, AD//BC (D) AB =CD,AD//BC
D
第七章 实数
1.了解无理数与实数的概念,学会区分无理数与有理数,会对实数进行分类.
2.了解算术平方根,平方根,立方根的概念,会用根号表示数的平方根立方根,掌握三者的区别.
3.掌握勾股定理及其逆定理的内容.会用勾股定理解决实际问题,会用逆定理判定直角三角形(难点).
算术平方根
负的平方根
你知道算术平方根、平方根、立方根联系和区别吗?
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开
方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有三种情况
1.把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
有理数集合
无理数集合
不要遗漏
2.解方程:
当方程中出现平方时,若有解,一般都有两个解
解:
3.
位置如图所示,
试化简
解:原式=-a-(b-a)+(c-a)-(c-b)
=-a-b+a+c-a-c+b=-a
勾股定理 逆定理
两直角边的平方和等于斜边的平方即
若三角形的三边满足
则三角形是直角三角形
是直角三角形的性质
用来判定三角形是否是直角三角形
内容
用途
勾股定理与逆定理
2、直角三角形两条直角边的长为
1和 ,求斜边上的高。
1、三角形三边 a,b,c满足
则此三角形为________________.
等腰直角三角形
在Rt⊿ABC其中两边 a,b满足
则此三角形c边长为________________.
不等号的两边都是整式,而且只有一个未知数,未知数的最高次数是一次
数轴、定点、定方向
用不等号连接而成的数学式子叫做不等式
1、不等号:
表示不等关系的符号称为不等号。一般包括“>”、“<”、“≥”、“≤”、“≠”五种,其意义、读法如下表所示:
名称 符号 读法 意义 例子
大于号
>
大于
左边的量大于右边的量
3>2
小于号
<
小于
左边的量小于右边的量
-5<1
大于或等于号
1.大于或等于
2.不小于
左边的量不小于右边的量
a≥4
≤
≥
≠
小于或等于号
1.小于或等于
2.不大于
左边的量不大于右边的量
不等号
不等于
左右两边的量不相等
b≤-1
c≠0
例:用不等号表示下列两数或两式的关系:
(1)3____-1;(2)-10____0;(3)2x2_____0;(4)|2x|______|-3x|.
>
<
≥
≤
3.不等到式的基本性质:
性质1:不等式的两边都加上(或减去)同一个整式,不等号的方向不变.
性质2:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
性质 3:不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.
注:在不等式两边都乘以(或除以)同一个整式时,应考虑整式为正数、负数、零三种情况。
4、不等式的解:
使不等式成立的未知数的值.
5、不等式的解集:
一个含有未知数的不等式的所有解,组成了这个不等式的解集。
6、解不等式:
求不等式解集的过程
其实质就是把不等式化为“x>a或x≥a或x
大于向右画,小于向左画.
a
x>a
a
x
x≥a
a
x≤a
8、不等式解集中最值问题:
对于不等式x≥a的解集有最小值,最小值为x=a;对于不等式x≤a的解集有最大值,最大值为x=a,而不等式x>a的解集没有最小值,x
解:根据已知条件,得a=2,b=5则ba=52=25
9、一元一次不等式:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
解一元一次不等式和解一元一次方程类似,有
去分母 去括号 移项 合并同类项
系数化为1等步骤.
与一元一次方程解法区别在哪里
在系数化为1的这一步中,要特别注意不等式的两边都乘以(或除以)一个负数时,不等号的方向必须改变方向.
10、一元一次不等式的解法
求不等式 3x+1≥4x-5的正整数解.
移项得:
合并同类项得:
化系数为1得:
解:
3x﹣4x≥-5-1
﹣x ≥-6
x≤6
所以不等式 的正整数解为:1、2、3、4、5、6
11、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组。
12、一元一次不等式组的解集:
一般地,一元一次不等式组中各个不等式解集的公共部分,叫这个一元一次不等式组的解集。
13、一元一次不等式组的解集的取法:
最简不等式组(a
x>b
x
x
a
b
a
b
a
b
a
b
x>b
x
同大取大
同小取小
大小小大取中间
大大小小解不了
14、一元一次不等式组的解法:
步骤:(1)先分别解不等式组中的每一个不等式,分别求出它们的解集;
(2)将每个不等式的解集在同一条数轴上表示出来,找出它们的公共部分,注意:公共部分可能没有,也可能是一个点。
(3)根据公共部分写出不等式组的解集,若没有公共部分,则说明不等式组无解。
特别注意:用数轴表示不等式的解集时,” <、>“用空心,” ≤、≥“用实心。” >、≥“向右画,” <、≤“向左画。
不等式(组)在实际生活中的应用
当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
15、一元一次不等式(组)的应用:
(1)利用不等式解决商家销售中的利润问题:
例:某商店将一件商品的进价提价20%的,再降价30%,以105元出售,问该商店卖出这件产品,是盈利还是亏损?
解:设这件商品的进价为x元,
则x(1+20%)(1-30%)=105,
解得x=125,因为105<125,
所以该商店卖出这件产品亏损了。
(2)利用不等式解决方案设计问题:
例:某校在“五一”期间组织学生外出旅游,如果单独租用45座的客车若干辆,恰好坐满;如果单独租用60座的客车,可少租一辆,并且有一辆不空也不满。
(1)求外出旅游的学生人数是多少?
(2)已知45座客车座客车每辆租金250元,60座客车每辆租金300元,为了节省租金,并保证每个学生都能有座,决定怎样租用客车,使得租金最少?
解:设单独租用45座的客车x辆,则单独租用了(x-1)辆60座的客车。根据题意得:
0<45x-60(x-2)<60
解得:4
去分母
去括号
移项
合并同类项
未知数的系数化为1
注意用不等式性质3,即不等式两边乘或
除以一个负数时,改变不等号的方向。
返回
类型(a>b) 解集 数轴显示 语言叙述
两大选取大
两小应选小
大于小小于大中间找
小于小大于大无处挑
a
b
a
b
a
b
a
b
x>a
b
返回
列一元一次不等式组解应用题
的一般步骤:
(1)审:审题,分析题目中已知什么,求什么,明确 各数量之间的关系;
(2)设:设适当的未知数;
(3)找:找出题目中的所有不等关系;
(4)列:列不等式组;
(5)解:求出不等式组的解集
(6)答:写出符合题意的答案
返回
二次根式
性质
运算
概念
二次根式
最简二次根式
同类二次根式
二次根式的概念
形如 (a 0)的式子
叫做二次根式
1.二次根式的定义:
2.二次根式的识别:
(1)被开方数
(2)根指数是2
题型1:确定二次根式中被开方数所含字母的取值范围.
1. 当 X _____时, 有意义。
3.求下列二次根式中字母的取值范围
解得 - 5≤x<3
解:
①
②
说明:二次根式被开方数不小于0,所以求二次根式中字母的取值范围常转化为不等式(组)
≤3
a=4
2. +
有意义的条件是
题型2:二次根式的非负性的应用.
1.已知: + =0,求 x-y 的值.
2.已知x,y为实数,且
+3(y-2)2 =0,则x-y的值为( )
A.3 B.-3 C.1 D.-1
解:由题意,得 x-4=0 且 2x+y=0
解得 x=4,y=-8
x-y=4-(-8)= 4+8 =12
D
注意:几个非负数的和为0,则每一个非负数必为0。
题型3:最简二次根式:
1、被开方数不含分数;
2、被开方数不含开的尽方的因数或因式;
注意:分母中不含二次根式。
化简二次根式的方法:
(1)如果被开方数是整数或整式时,先因数分解或因式分解,然后利用积的算术平方根的性质,将式子化简。
(2)如果被开方数是分数或分式时,先利用商的算术平方根的性质,将其变为二次根式相除的形式,然后利用分母有理化,将式子化简。
题型4:利用
进行分解因式
例:分解因式:
1.回顾并理解掌握正比例函数、一次函数的概念、图象、性质
及解析式的确定,查漏补缺;理解回顾一次函数与一元一次
方程、一元一次不等式、二元一次方程组的关系。会用相关
知识解决实际问题。
2.提升学生自主构建知识体系的能力,进一步提高学生数形结
合思想和用函数思想解决问题的能力。
3.在学习过程中,培养学生独立思考、合作探究的意识和能力,
进一步激发学生学习数学的兴趣。
1.一次函数的图象及性质的归纳和总结.
2.通过一次函数图象深刻认识方程(组)、
不等式(组)的解.
3.运用一次函数的图象及其性质解决有关实际问题.
1.一次函数的实际应用.
2. 函数思想、数形结合的渗透和应用.
变化的
世界
函数
定义
函数关系的表示方法
图象法
列表法
表达式
一
次
函
数
定义
图象
性质
函数与一元一次方程(组)的关系
函数与一元一次不等式的关系
应用
Y=kx+b(k≠0)
直线
对应性
增减性
实际应用
待定系数法
正比例函数
(1)在某一问题中,保持 的量叫常量,可以取 的量,叫做变量.
不变
不同数值
(2)函数:在同一变化过程中,有两个变量x和y,如果对于x的每—个值,y都有______________与之对应,我们就把y叫做x的函数,其中x叫做自变量.如果自变量x取a时,y的值是b,就把b叫做x=a时的函数值.
唯一确定的值
一、知识要点
(3)函数的图象:用图像表示变量之间函数关系的方法叫做图象法
1. 函数的概念
一次函数的概念:如果函数y=_______(k、b为常数,且k______),那么y叫做x的一次函数。
kx +b
≠0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴解析式中自变量x的次数是___次,
⑵比例系数_____。
1
k≠0
特别地,当b_____时,函数y=____(k____)叫做正比例函数。
= 0
2.一次函数的概念
a. 正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
b.一次函数y=kx+b(k≠0)的图象是过点(0,___),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
>
>
>
<
<
<
<
>
2.一次函数的图象
c.一次函数y=kx+b(k≠0)的图象与k,b符号的关系:
一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
增大
减小
3.一次函数的性质
(1)增减性
从表中可以看出:由一次函数经过的象限可以判断k、b的符号,
反过来,由k、b的符号也可以判断图象经过的象限.
(2)k.b的符号与图象所在位置对应性
以二元一次方程的解为坐标的点都在对应一次函数的图像上;
以一次函数的图像上点的坐标都是对应二元一次方程的解。
4.一次函数与二元一次方程组的关系(对应性)
. 二元一次方程组的解与以这两个方程
所对应的一次函数图象的交点坐标相对应。
解:把x=1时, y=5;x=6时,y=0分别代入解析式,得
解得
∴此一次函数的解析式为 y= - x+6
用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
例:已知一次函数y=kx+b(k≠0)当x=1时,y=5,且它的图象与x轴交点的横坐标是6,求这个一次函数的解析式。
5.一次函数的应用
(1)待定系数法:
一.使用直译法求解一次函数应用题
所谓直译法就是将题中的关键语句“译”成代数式,然后找出函数关系、列出一次函数解析式,从而解决问题的方法。
二.使用列表法求解一次函数应用题
列表法就是将题目中的各个量列成一个表格,从而理顺它们之间的数量关系,以便于从中找到函数关系的解题方法。
三.使用图示法求解一次函数应用题
所谓图示法就是用图形来表示题中的数量关系,从而观察出函数关系的解题方法。
此法对于某些一次函数问题非常有效,解题过程直观明了。
小结
1.一次函数的概念;
2.一次函数的图象;
3.一次函数的性质;
5. 一次函数的与方程、方程组及不等式的关系
4. 一次函数的应用
(1)待定系数法;
(2)利用一次函数解决实际问题。
第十一章
旋转前后的图形完全重合
轴对称图形
中心对称图形
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕对称中心旋转
180°
3
翻转前后的图形完全重合
E
H
F
G
1、如图,正方形EFGH是由正方形ABCD平移得到的, 则有( )
A.点E和B对应 B. 线段AD和EH对应
C. 线段AC和FH对应 D. ∠B和∠D对应
A
B
C
D
B
平移方向和距离呢?
2、如图△ABC是等腰直角三角形, 点D是斜边BC中点, △ABD绕点A旋转到△ACE的位置, 恰与△ACD组成正方形ADCE, 则△ABD所经过的旋转是( )
B
C
D
E
A
A. 顺时针旋转225° B. 逆时针旋转45°
C. 顺时针旋转315° D. 逆时针旋转90°
D
3、下列图形中,既是轴对称图形又是中心对称图形的是( )
(A)
(B)
(C )
(D)
D
4、已知四边形ABCD和点O,画四边形A'B'C'D' 使它与已知四边形关于点O对称。
A
B
C
D
O
A'
B'
C'
D'
画法:
四边形A'B'C'D'就是所求的四边形。
5. 下列说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
B
谈谈你本节课的收获是什么?
同课章节目录
