青岛版八年级数学下册 10.5一次函数与一元一次不等式 教学设计
文档属性
| 名称 | 青岛版八年级数学下册 10.5一次函数与一元一次不等式 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 374.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-23 15:21:47 | ||
图片预览

文档简介
《一次函数与一元一次不等式》教学设计
【目标设计】
①经历不等式与函数问题的探讨过程,学习用联系的观点看待数学问题的辨证思想。理解一次函数与一元一次不等式的关系。会根据一次函数图像解决一元一次不等式解的问题。
②学习用函数的观点看待不等式的方法,初步形成用全面的观点处理局部问题。
③增强学生学数学,用数学,探索数学奥妙的愿望,体验成功的感觉,品尝成功的喜悦。
【过程设计】
一、热身活动:
在右图直角坐标系中做出函数y=2x+4的图象.
(1)方程2x+4=0的解是
(2)图象与x轴的交点坐标是 .
(3)图象与x轴的交点(重点研究)
①把x轴分成了两部分: 和________.
②把直线y=2x+4分成两部分:
在x轴的上方的部分的点的坐标特点是_______.
在x轴的下方的部分的点的坐标特点是_______.
二、探究一:求不等式2x+4>0的解集
1.方法一:解不等式2x+4>0得x>-2
2.方法二:运用函数的观点,利用函数y=2x+4
不等式 运用函数 转化 分界点 图象部分 x的取值
2x+4>0 y=2x+4 y>0 (-2,0) 分界点上方(x轴上方) x>-2
3.跟踪训练:解一元一次不等式:-3x+1<0
三、探究二:求不等式2x+4<1的解集
1.方法一:解不等式2x+4<1得x<
2.方法二:原不等式为2x+3<0,利用函数y=2x+3
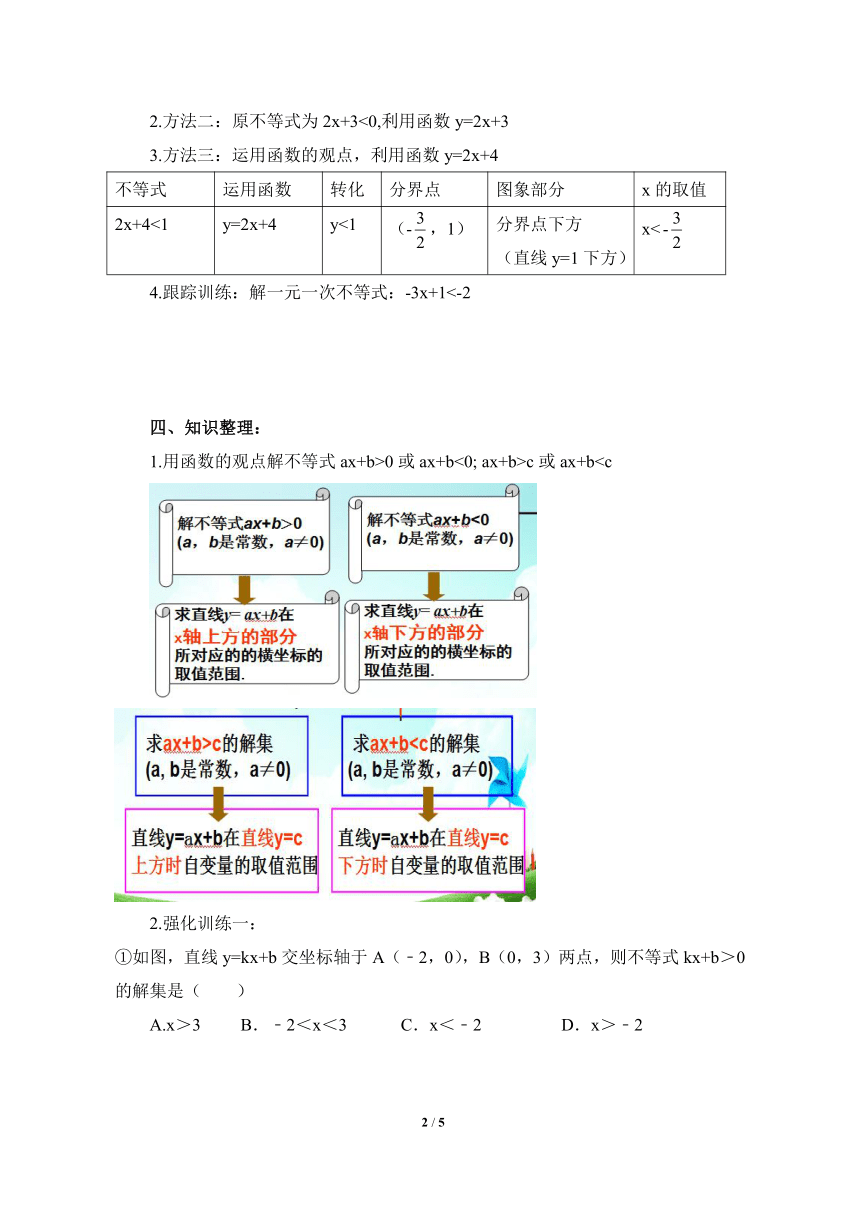
3.方法三:运用函数的观点,利用函数y=2x+4
不等式 运用函数 转化 分界点 图象部分 x的取值
2x+4<1 y=2x+4 y<1 (-,1) 分界点下方(直线y=1下方) x<
4.跟踪训练:解一元一次不等式:-3x+1<-2
四、知识整理:
1.用函数的观点解不等式ax+b>0或ax+b<0; ax+b>c或ax+b2.强化训练一:
①如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.﹣2<x<3 C.x<﹣2 D.x>﹣2
第1题图 第2题图 第3题图
②如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 .
③如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则关于x的不等式-2< kx+b <1的解集为______________.
五、探究三:求不等式- x+2>3x-3的解集
1.方法一:解不等式- x+2>3x-3得x<
2.方法二:将原不等式变形为:-4x-5>0,运用函数y=-4x-5
3.方法三:将原不等式变形为:-4x+2>-3,运用函数y=-4x+2
4.方法四:运用函数的观点,利用函数y1=-x+2,y2=3x-3
不等式 运用函数 转化 分界点 图象部分 x的取值
- x+2>3x-3 y1=-x+2,y2=3x-3 y1>y2 (,) 分界点左侧(交点左侧) x<
5.知识整理:
6.强化训练二:
①如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A.x>1 B.x>2 C.x<1 D.x<2
第1题图 第2题图
②如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
六、课堂聚集:
七、当堂检测:
1.如图,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是_______.
第1题图 第2题图 第3题图
2.如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,5)两点,则不等式-kx-b<0的解集为_________.
3.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为___________
八、课后提升
1.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为___________
2.直线y=kx+b经过A(3,1)和B(6,0)两点,不等式0<kx+b<x的解集为_______________
1 / 5
【目标设计】
①经历不等式与函数问题的探讨过程,学习用联系的观点看待数学问题的辨证思想。理解一次函数与一元一次不等式的关系。会根据一次函数图像解决一元一次不等式解的问题。
②学习用函数的观点看待不等式的方法,初步形成用全面的观点处理局部问题。
③增强学生学数学,用数学,探索数学奥妙的愿望,体验成功的感觉,品尝成功的喜悦。
【过程设计】
一、热身活动:
在右图直角坐标系中做出函数y=2x+4的图象.
(1)方程2x+4=0的解是
(2)图象与x轴的交点坐标是 .
(3)图象与x轴的交点(重点研究)
①把x轴分成了两部分: 和________.
②把直线y=2x+4分成两部分:
在x轴的上方的部分的点的坐标特点是_______.
在x轴的下方的部分的点的坐标特点是_______.
二、探究一:求不等式2x+4>0的解集
1.方法一:解不等式2x+4>0得x>-2
2.方法二:运用函数的观点,利用函数y=2x+4
不等式 运用函数 转化 分界点 图象部分 x的取值
2x+4>0 y=2x+4 y>0 (-2,0) 分界点上方(x轴上方) x>-2
3.跟踪训练:解一元一次不等式:-3x+1<0
三、探究二:求不等式2x+4<1的解集
1.方法一:解不等式2x+4<1得x<
2.方法二:原不等式为2x+3<0,利用函数y=2x+3
3.方法三:运用函数的观点,利用函数y=2x+4
不等式 运用函数 转化 分界点 图象部分 x的取值
2x+4<1 y=2x+4 y<1 (-,1) 分界点下方(直线y=1下方) x<
4.跟踪训练:解一元一次不等式:-3x+1<-2
四、知识整理:
1.用函数的观点解不等式ax+b>0或ax+b<0; ax+b>c或ax+b
①如图,直线y=kx+b交坐标轴于A(﹣2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.﹣2<x<3 C.x<﹣2 D.x>﹣2
第1题图 第2题图 第3题图
②如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 .
③如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则关于x的不等式-2< kx+b <1的解集为______________.
五、探究三:求不等式- x+2>3x-3的解集
1.方法一:解不等式- x+2>3x-3得x<
2.方法二:将原不等式变形为:-4x-5>0,运用函数y=-4x-5
3.方法三:将原不等式变形为:-4x+2>-3,运用函数y=-4x+2
4.方法四:运用函数的观点,利用函数y1=-x+2,y2=3x-3
不等式 运用函数 转化 分界点 图象部分 x的取值
- x+2>3x-3 y1=-x+2,y2=3x-3 y1>y2 (,) 分界点左侧(交点左侧) x<
5.知识整理:
6.强化训练二:
①如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A.x>1 B.x>2 C.x<1 D.x<2
第1题图 第2题图
②如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集在数轴上表示正确的是( )
A. B. C. D.
六、课堂聚集:
七、当堂检测:
1.如图,函数y=ax-1的图象过点(1,2),则不等式ax-1>2的解集是_______.
第1题图 第2题图 第3题图
2.如图,直线y=kx+b交坐标轴于A(-3,0)、B(0,5)两点,则不等式-kx-b<0的解集为_________.
3.如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,2),则关于x的不等式x+1≥mx+n的解集为___________
八、课后提升
1.如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b<0的解集为___________
2.直线y=kx+b经过A(3,1)和B(6,0)两点,不等式0<kx+b<x的解集为_______________
1 / 5
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
