1.2简单的轴对称图形(2)
图片预览

文档简介
“1.2简单的轴对称图形(2)”导学提纲
学习目标:
通过动手操作,理解线段的垂直平分线的性质,并初步掌握用尺规作线段的垂直平分线.
经历探索简单图形的轴对称性和线段垂直平分线的性质的过程,经历与他人合作交流的过程,进一步体验轴对称的特征,发展空间观念,增强审美意识.
教学过程:
一.自主探究:
1.预习疑难摘要①
2.猜想:线段是不是轴对称图形?它有几条对称轴?它的对称轴是什么?②
3.阅读课本P7
4.针对上述操作,思考如下问题:
(1)CO与AB的位置关系是
(2)线段AD与OB是否相等?线段CA与CB是否相等?请说明理由.
在折痕上另取一点,再试一试,你有什么发现?③
5.前面我们用折叠的方法得到线段垂直平分线,下面你能用直尺和圆规作出线段垂直平分线吗?
请同学们按如下作法进行操作:
已知:线段AB
求作:线段AB的垂直平分线
作法:
(1)分别以 和 为圆心,以 的长为半径作弧,两弧相较于 和
(2)作直线CD
则直线CD就是线段AB的垂直平分线
二.合作交流,成果展示:
1.小组代表到黑板演示折纸操作交流第4题答案④
2.请同学们针对第5题互相交流,说明直线CD是线段AB的垂直平分线用这种方法是否可以作线段的中点?⑤
3.结合上面的问题,说说线段的垂直平分线的概念:
4根据图形,用几何语言表达线段的垂直平分线的性质
因为
所以 ⑥
5.结合上面的问题,说说线段的垂直平分线的性质
⑦
6.思考:到线段两端点距离相等的点在这条线段的垂直平分线上吗?⑧
三.应用规律,巩固新知⑨
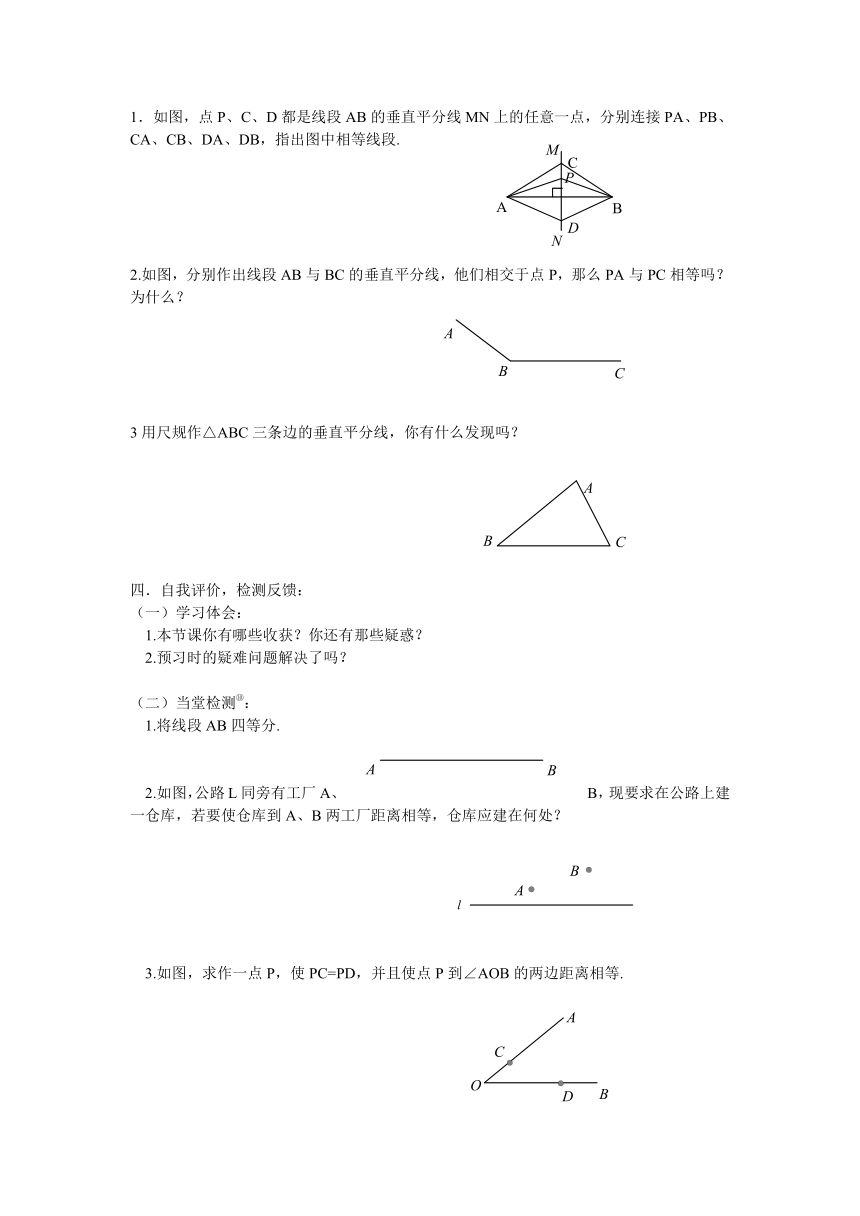
1.如图,点P、C、D都是线段AB的垂直平分线MN上的任意一点,分别连接PA、PB、CA、CB、DA、DB,指出图中相等线段.
2.如图,分别作出线段AB与BC的垂直平分线,他们相交于点P,那么PA与PC相等吗?为什么?
3用尺规作△ABC三条边的垂直平分线,你有什么发现吗?
四.自我评价,检测反馈:
(一)学习体会:
1.本节课你有哪些收获?你还有那些疑惑?
2.预习时的疑难问题解决了吗?
(二)当堂检测⑩:
1.将线段AB四等分.
2.如图,公路L同旁有工厂A、B,现要求在公路上建一仓库,若要使仓库到A、B两工厂距离相等,仓库应建在何处?
3.如图,求作一点P,使PC=PD,并且使点P到∠AOB的两边距离相等.
(3三)课外自评:
1.(必做)课本练习P9 2 、3.、4
2.(选做)如图所示,点A为∠MON内的一点,试在OM、ON边上分别作出两点B、C,使△ABC的周长最小,并说明理由.
五.教(学)后反思
“1.2简单的轴对称图形(2)“导学提纲
设计意图与教学建议
经历探索简单 经历探索简单图形的轴对称的过程,进一步探索并了解角的平分线的有关性质,初步掌握用尺规作线段的垂直平分线,培养学生动手操作、观察分析和发现问题的能力.
①了解学生预习过程的疑难,也有利于学生在自学中动脑思考.
②让学生在实际操作中探索线段的垂直平分线的相关性质,培养学生的猜想观察、动手操作能力
③发展学生观察能力,概括归纳能力,感受由特殊到一般的思想方法.
④这是学习的重点,锻炼学生的画图能力
⑤通过相互交流,体现师生互动、生生互动
⑥这是学习的重点,先采用观察图形,用几何语言表达的方式发展学生的形象思维.
⑦可以采用启发,引导的方式总结角平分线的性质,发展学生的抽象思维和有条理的表达能力
⑧将性质中的条件和结论颠倒,让学生判断正误,为下面的当堂检测第3题做铺垫.
⑨线段垂直平分线性质的运用是本节的难点,第二题是性质的运用,第3题是性质运用和画法的综合,第4题作为对学有余力的学生学习的补充.
⑩检测学生对线段垂直平分线性质基本类型题的掌握.
自主探究时间:学生课前预习
合作交流、成果展示时间:15分钟
应用规律、巩固新知时间:18分钟
自我评价、检测反馈时间:12分钟
学习目标:
通过动手操作,理解线段的垂直平分线的性质,并初步掌握用尺规作线段的垂直平分线.
经历探索简单图形的轴对称性和线段垂直平分线的性质的过程,经历与他人合作交流的过程,进一步体验轴对称的特征,发展空间观念,增强审美意识.
教学过程:
一.自主探究:
1.预习疑难摘要①
2.猜想:线段是不是轴对称图形?它有几条对称轴?它的对称轴是什么?②
3.阅读课本P7
4.针对上述操作,思考如下问题:
(1)CO与AB的位置关系是
(2)线段AD与OB是否相等?线段CA与CB是否相等?请说明理由.
在折痕上另取一点,再试一试,你有什么发现?③
5.前面我们用折叠的方法得到线段垂直平分线,下面你能用直尺和圆规作出线段垂直平分线吗?
请同学们按如下作法进行操作:
已知:线段AB
求作:线段AB的垂直平分线
作法:
(1)分别以 和 为圆心,以 的长为半径作弧,两弧相较于 和
(2)作直线CD
则直线CD就是线段AB的垂直平分线
二.合作交流,成果展示:
1.小组代表到黑板演示折纸操作交流第4题答案④
2.请同学们针对第5题互相交流,说明直线CD是线段AB的垂直平分线用这种方法是否可以作线段的中点?⑤
3.结合上面的问题,说说线段的垂直平分线的概念:
4根据图形,用几何语言表达线段的垂直平分线的性质
因为
所以 ⑥
5.结合上面的问题,说说线段的垂直平分线的性质
⑦
6.思考:到线段两端点距离相等的点在这条线段的垂直平分线上吗?⑧
三.应用规律,巩固新知⑨
1.如图,点P、C、D都是线段AB的垂直平分线MN上的任意一点,分别连接PA、PB、CA、CB、DA、DB,指出图中相等线段.
2.如图,分别作出线段AB与BC的垂直平分线,他们相交于点P,那么PA与PC相等吗?为什么?
3用尺规作△ABC三条边的垂直平分线,你有什么发现吗?
四.自我评价,检测反馈:
(一)学习体会:
1.本节课你有哪些收获?你还有那些疑惑?
2.预习时的疑难问题解决了吗?
(二)当堂检测⑩:
1.将线段AB四等分.
2.如图,公路L同旁有工厂A、B,现要求在公路上建一仓库,若要使仓库到A、B两工厂距离相等,仓库应建在何处?
3.如图,求作一点P,使PC=PD,并且使点P到∠AOB的两边距离相等.
(3三)课外自评:
1.(必做)课本练习P9 2 、3.、4
2.(选做)如图所示,点A为∠MON内的一点,试在OM、ON边上分别作出两点B、C,使△ABC的周长最小,并说明理由.
五.教(学)后反思
“1.2简单的轴对称图形(2)“导学提纲
设计意图与教学建议
经历探索简单 经历探索简单图形的轴对称的过程,进一步探索并了解角的平分线的有关性质,初步掌握用尺规作线段的垂直平分线,培养学生动手操作、观察分析和发现问题的能力.
①了解学生预习过程的疑难,也有利于学生在自学中动脑思考.
②让学生在实际操作中探索线段的垂直平分线的相关性质,培养学生的猜想观察、动手操作能力
③发展学生观察能力,概括归纳能力,感受由特殊到一般的思想方法.
④这是学习的重点,锻炼学生的画图能力
⑤通过相互交流,体现师生互动、生生互动
⑥这是学习的重点,先采用观察图形,用几何语言表达的方式发展学生的形象思维.
⑦可以采用启发,引导的方式总结角平分线的性质,发展学生的抽象思维和有条理的表达能力
⑧将性质中的条件和结论颠倒,让学生判断正误,为下面的当堂检测第3题做铺垫.
⑨线段垂直平分线性质的运用是本节的难点,第二题是性质的运用,第3题是性质运用和画法的综合,第4题作为对学有余力的学生学习的补充.
⑩检测学生对线段垂直平分线性质基本类型题的掌握.
自主探究时间:学生课前预习
合作交流、成果展示时间:15分钟
应用规律、巩固新知时间:18分钟
自我评价、检测反馈时间:12分钟
