8.2 一元线性回归模型及其应用 第八章 成对数据的统计分析 人教A版选择性必修第三册 课件(共55张PPT)
文档属性
| 名称 | 8.2 一元线性回归模型及其应用 第八章 成对数据的统计分析 人教A版选择性必修第三册 课件(共55张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-03-25 00:00:00 | ||
图片预览










文档简介
(共55张PPT)
8.2 一元线性回归模型及其应用
学习指导 核心素养
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义. 2.了解最小二乘原理,掌握求一元线性回归模型参数的最小二乘估计,会使用相关的统计软件,针对实际问题,会用一元线性回归模型进行预测. 1.数学抽象:一元线性回归模型.
2.数学建模、数学运算:一元线性回归模型参数的最小二乘估计.
Y
x
截距
斜率
经验回归方程
经验回归直线
观测值
预测值
观测值
预测值
1.在一元线性回归模型y=bx+a+e中,随机误差e产生的原因有哪些?
提示:(1)所用的确定性函数不恰当引起的误差;
(2)忽略了某些因素的影响;
(3)存在观测误差.
2.经验回归直线一定过成对样本数据(x1,y1),(x2,y2),…,(xn,yn)中的某一点吗?
×
√
√
√
√
√
3.为研究两个变量之间的关系,选择了4个不同的模型进行拟合,计算得它们的决定系数R2,其中拟合效果最好的模型是( )
A.决定系数R2为0.96
B.决定系数R2为0.75
C.决定系数R2为0.52
D.决定系数R2为0.34
解析:决定系数R2越大、越趋近于1,拟合效果越好.
√
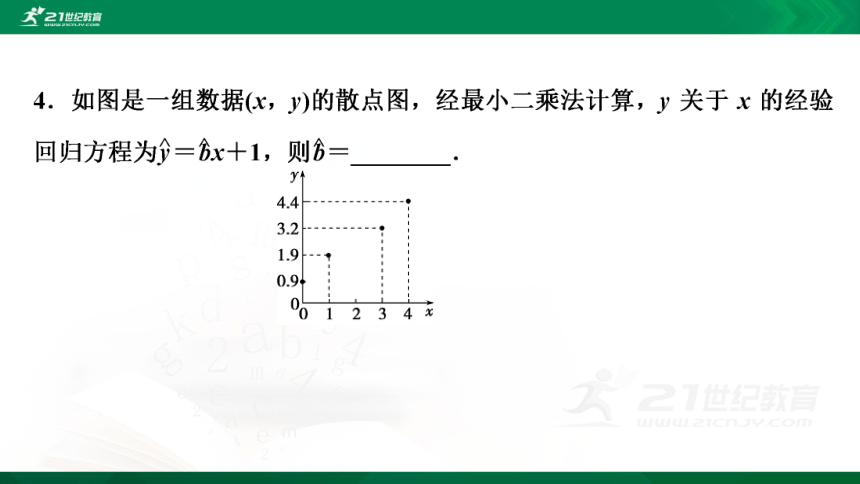
答案:0.8
探究点1 经验回归方程
[问题探究]
利用经验回归方程进行预测所得值精确吗?
探究感悟:(1)所得的值只是一个估计值,不是精确值;
(2)变量x与y成线性相关关系时,经验回归方程才有意义,否则即使求出经验回归方程,也是毫无意义的,用其估计和预测的量也是不可信、无价值的.
【解】 (1)散点图如图所示,
(1)求z关于t的经验回归方程;
(2)通过(1)中的方程,求出y关于x的经验回归方程;
(3)用所求经验回归方程预测到2022年年底,该地此银行储蓄存款额可达到多少?
t 1 2 3 4 5
z 0 1 2 3 5
探究点2 线性回归分析
[问题探究]
对一个问题的回归模型,怎样刻画回归的效果?
探究感悟:有三种方式刻画回归效果:(1)残差图法;(2)残差平方和法;(3)决定系数R2.
(3)由残差表中的数值可以看出第3个样本点的残差比较大,需要确认在采集这个数据的时候是否有人为的错误,如果有的话,需要纠正数据,重新建立回归模型;由表中数据可以看出残差点比较均匀地落在不超过0.15的狭窄的水平带状区域中,说明选用的回归模型的精度较高,由以上分析可知,弹簧长度与质量成线性关系.
对回归模型进行回归分析的方法
(1)残差平方和越小,模型的拟合效果越好.
(2)决定系数R2越大,说明模型的拟合效果越好.
需要注意的是:若题中给出了检验回归方程是否理想的条件,则根据题意进行分析检验即可.
探究点3 非线性回归分析
[问题探究]
有些成对变量的散点图并不具有线性回归的特征,应怎样处理?
探究感悟:可通过散点图选择适当类型的拟合函数,通过对变量的变换转化成线性回归模型解决.常见的拟合函数有(1)指数型函数:y=ebx+a类;(2)对数型函数:y=bln x+a类;(3)幂函数型:y=bxα+a类.
解决非线性回归问题的步骤
某地今年上半年患某种传染病的人数y(人)与月份x(月)之间满足函数关系,模型为y=aebx,确定这个函数解析式.
月份x/月 1 2 3 4 5 6
人数y/人 52 61 68 74 78 83
√
√
√
3.(2021·重庆高二期末)若某地财政收入x与支出y满足一元线性回归模型y=bx+a+e(单元:亿元),其中b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
A.9亿元 B.9.5亿元
C.10亿元 D.10.5亿元
√
解析:因为财政收入x与支出y满足一元线性回归模型y=bx+a+e,
其中b=0.7,a=3,所以得到y=0.7 x+3+e,
当x=10时,得y=0.7×10+3+e=10+e,
而|e|≤0.5,即-0.5≤e≤0.5,所以9.5≤y≤10.5,
所以年支出预计不会超过10.5亿元.故选D.
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
8.2 一元线性回归模型及其应用
学习指导 核心素养
1.结合具体实例,了解一元线性回归模型的含义,了解模型参数的统计意义. 2.了解最小二乘原理,掌握求一元线性回归模型参数的最小二乘估计,会使用相关的统计软件,针对实际问题,会用一元线性回归模型进行预测. 1.数学抽象:一元线性回归模型.
2.数学建模、数学运算:一元线性回归模型参数的最小二乘估计.
Y
x
截距
斜率
经验回归方程
经验回归直线
观测值
预测值
观测值
预测值
1.在一元线性回归模型y=bx+a+e中,随机误差e产生的原因有哪些?
提示:(1)所用的确定性函数不恰当引起的误差;
(2)忽略了某些因素的影响;
(3)存在观测误差.
2.经验回归直线一定过成对样本数据(x1,y1),(x2,y2),…,(xn,yn)中的某一点吗?
×
√
√
√
√
√
3.为研究两个变量之间的关系,选择了4个不同的模型进行拟合,计算得它们的决定系数R2,其中拟合效果最好的模型是( )
A.决定系数R2为0.96
B.决定系数R2为0.75
C.决定系数R2为0.52
D.决定系数R2为0.34
解析:决定系数R2越大、越趋近于1,拟合效果越好.
√
答案:0.8
探究点1 经验回归方程
[问题探究]
利用经验回归方程进行预测所得值精确吗?
探究感悟:(1)所得的值只是一个估计值,不是精确值;
(2)变量x与y成线性相关关系时,经验回归方程才有意义,否则即使求出经验回归方程,也是毫无意义的,用其估计和预测的量也是不可信、无价值的.
【解】 (1)散点图如图所示,
(1)求z关于t的经验回归方程;
(2)通过(1)中的方程,求出y关于x的经验回归方程;
(3)用所求经验回归方程预测到2022年年底,该地此银行储蓄存款额可达到多少?
t 1 2 3 4 5
z 0 1 2 3 5
探究点2 线性回归分析
[问题探究]
对一个问题的回归模型,怎样刻画回归的效果?
探究感悟:有三种方式刻画回归效果:(1)残差图法;(2)残差平方和法;(3)决定系数R2.
(3)由残差表中的数值可以看出第3个样本点的残差比较大,需要确认在采集这个数据的时候是否有人为的错误,如果有的话,需要纠正数据,重新建立回归模型;由表中数据可以看出残差点比较均匀地落在不超过0.15的狭窄的水平带状区域中,说明选用的回归模型的精度较高,由以上分析可知,弹簧长度与质量成线性关系.
对回归模型进行回归分析的方法
(1)残差平方和越小,模型的拟合效果越好.
(2)决定系数R2越大,说明模型的拟合效果越好.
需要注意的是:若题中给出了检验回归方程是否理想的条件,则根据题意进行分析检验即可.
探究点3 非线性回归分析
[问题探究]
有些成对变量的散点图并不具有线性回归的特征,应怎样处理?
探究感悟:可通过散点图选择适当类型的拟合函数,通过对变量的变换转化成线性回归模型解决.常见的拟合函数有(1)指数型函数:y=ebx+a类;(2)对数型函数:y=bln x+a类;(3)幂函数型:y=bxα+a类.
解决非线性回归问题的步骤
某地今年上半年患某种传染病的人数y(人)与月份x(月)之间满足函数关系,模型为y=aebx,确定这个函数解析式.
月份x/月 1 2 3 4 5 6
人数y/人 52 61 68 74 78 83
√
√
√
3.(2021·重庆高二期末)若某地财政收入x与支出y满足一元线性回归模型y=bx+a+e(单元:亿元),其中b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入10亿元,年支出预计不会超过( )
A.9亿元 B.9.5亿元
C.10亿元 D.10.5亿元
√
解析:因为财政收入x与支出y满足一元线性回归模型y=bx+a+e,
其中b=0.7,a=3,所以得到y=0.7 x+3+e,
当x=10时,得y=0.7×10+3+e=10+e,
而|e|≤0.5,即-0.5≤e≤0.5,所以9.5≤y≤10.5,
所以年支出预计不会超过10.5亿元.故选D.
【戮力同心 共赴前程】
生如蝼蚁当立鸿鹄之志
命如纸薄应有不屈之心
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
