4.2.1直线与圆的位置关系
图片预览






文档简介
课件21张PPT。4.2.1直线与圆的位置关系 湖南省耒阳市振兴学校
高中数学老师欧阳文丰制作直线与圆的位置关系知识回顾直线方程的一般式为:____________________________2.圆的标准方程为:______________3.圆的一般方程:__________________________________ 圆心为________半径为______Ax+By+C=0(A,B不同时为零)(x-a)2+(y-b)2=r2x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0)
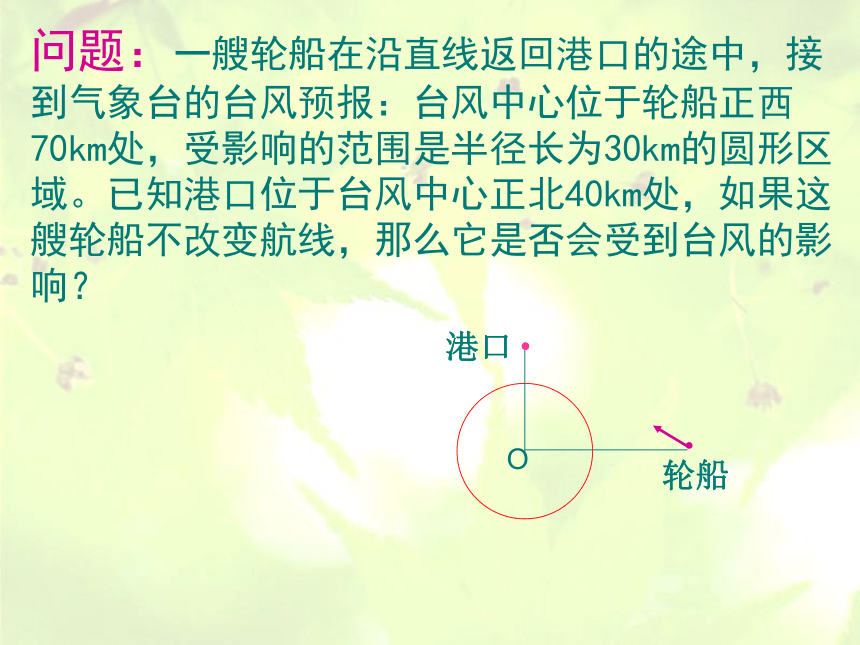
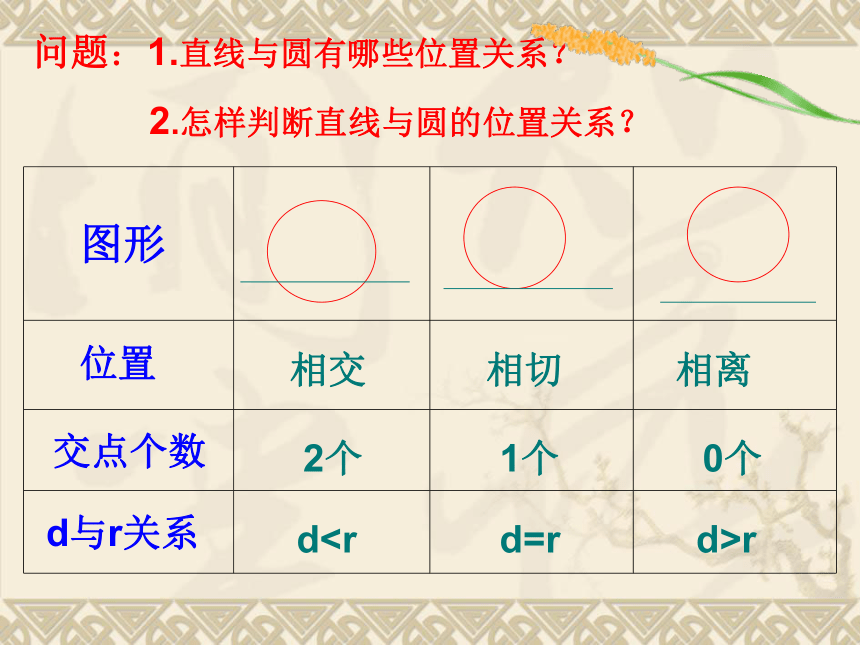
圆心为 半径为(a,b)r问题:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响? .轮船港口O直线与圆的位置关系问题1:你知道直线和圆的位置关系有几种?知识点拨图形问题:1.直线与圆有哪些位置关系?
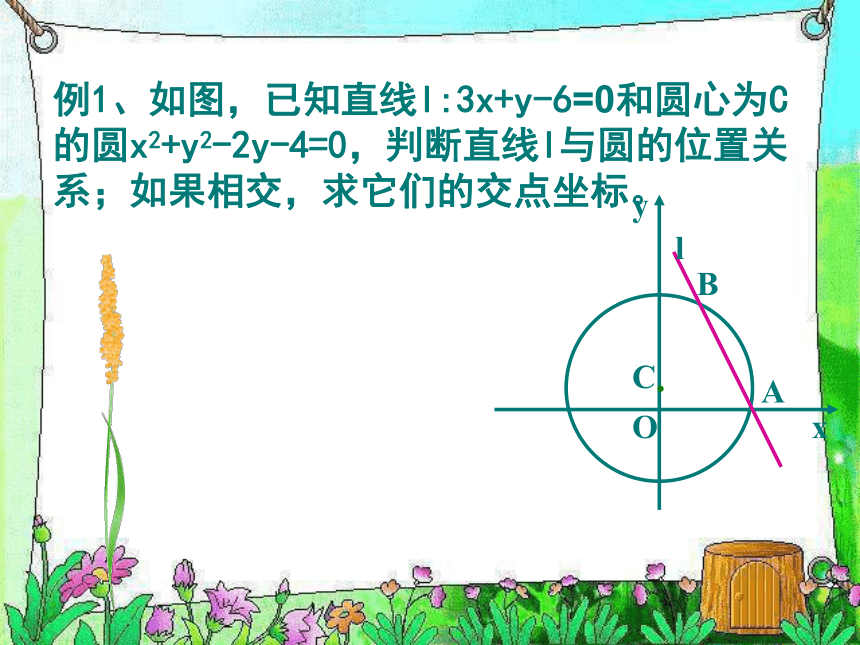
2.怎样判断直线与圆的位置关系?交点个数d与r关系dr例1、如图,已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。解法二:圆 可化为
其圆心C的坐标为(0,1),半径为 ,点C(0,1)到直线 的距离
所以,直线 与圆相交,有两个公共点 由 ,解得
把 代入方程①,得
把 代入方程①,得
所以,直线 与圆由两个交点,它们
的坐标分别是A(2,0), B(1,3)(2)利用圆心到直线的距离d与半径r的大小关系判断:小结:直线与圆的位置关系的判定方法。(1)利用直线与圆的交点的个数进行判断:例2、已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程。解:将圆的方程写成标准形式,得
所以,圆心的坐标是 ,半径长
如图,因为直线 所截的弦长是 ,所以弦心距为
即圆心到所求直线 的距离为
因为直线 过点 ,所以可设所求直线 的方程为
即
根据点到直线的距离公式,得到圆心到直线 的距离
因此, 即
两边平方,并整理得到
解得 ,或
所以,所求直线 有两条,它们的方程分别为
或
即 或
例3 设直线 和圆 相切,
求实数m的值。 解法一:已知圆的圆心为O( 0, 0), 半径r =1,
则O到已知直线的距离
由已知得 d=r , 即
解得 m=④试解本节引言中的问题. 解:以台风中心为原点,东西方向为x 轴,建立如图所示的直角坐标系,其中,取10km为单位长度,这样,受台风影响的圆形区域所对应的圆O方程为
轮船航线所在直线L的方程为4x+7y-28=0
?问题归结为圆O与直线L有无公共点。
点O到直线L的距离
圆O的半径长r=3
因为3.5>3,所以,这艘轮船不必改变航线,不会受到台风的影响.
xy0AB1、直线和圆相离2、直线和圆相切3、直线和圆相交直线与圆的位置关系图形圆心到直线距离 d 与圆半径r之间关系几何方法代数方法无交点时有一个交点时有两个交点时课堂总结 作业: 习题 4.2
第3题 第5题归纳小结1:过圆x2+y2=r2上一点(xo,yo)的切线方程为xox+yoy=r2
2:过圆(x-a)2+(y-b)2=r2上一点(xo,yo)的切线方程为(x-a)(x-x0)+(y-b)(y-y0)=r2
3:过圆x2+y2=r2外一点(xo,yo)的作圆的切线,两切点的连线的直线方程为xox+yoy=r2
4:过圆(x-a)2+(y-b)2=r2外一点(xo,yo)的作圆的切线,两切点的连线的直线方程为
(x-a)(x-x0)+(y-b)(y-y0)=r2
补充习题.己知圆C: x2+y2-2x-4y-20=0,
直线l: (2m+1)x+(m+1)y-7m-4=0(m∈R)
(1)证明: 无论m取何值 直线l与圆C恒相交.
(2)求直线l被圆C截得的最短弦长,及此时
直线l的方程.分析: 若直线经过圆内
的一定点,那么该直线
必与圆交于两点,因此
可以从直线过定点的角
度去考虑问题. 提高练习 解 (1)将直线l的方程变形,得
m(2x+y-7)+(x+y-4)=0.
∵对于任意的实数m, 方程都成立,此时l方程 y -1 = 2 (x - 3),即 2x-y-5=0
高中数学老师欧阳文丰制作直线与圆的位置关系知识回顾直线方程的一般式为:____________________________2.圆的标准方程为:______________3.圆的一般方程:__________________________________ 圆心为________半径为______Ax+By+C=0(A,B不同时为零)(x-a)2+(y-b)2=r2x2+y2+Dx+Ey+F=0(其中D2+E2-4F>0)
圆心为 半径为(a,b)r问题:一艘轮船在沿直线返回港口的途中,接到气象台的台风预报:台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域。已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响? .轮船港口O直线与圆的位置关系问题1:你知道直线和圆的位置关系有几种?知识点拨图形问题:1.直线与圆有哪些位置关系?
2.怎样判断直线与圆的位置关系?交点个数d与r关系d
其圆心C的坐标为(0,1),半径为 ,点C(0,1)到直线 的距离
所以,直线 与圆相交,有两个公共点 由 ,解得
把 代入方程①,得
把 代入方程①,得
所以,直线 与圆由两个交点,它们
的坐标分别是A(2,0), B(1,3)(2)利用圆心到直线的距离d与半径r的大小关系判断:小结:直线与圆的位置关系的判定方法。(1)利用直线与圆的交点的个数进行判断:例2、已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为 ,求直线l的方程。解:将圆的方程写成标准形式,得
所以,圆心的坐标是 ,半径长
如图,因为直线 所截的弦长是 ,所以弦心距为
即圆心到所求直线 的距离为
因为直线 过点 ,所以可设所求直线 的方程为
即
根据点到直线的距离公式,得到圆心到直线 的距离
因此, 即
两边平方,并整理得到
解得 ,或
所以,所求直线 有两条,它们的方程分别为
或
即 或
例3 设直线 和圆 相切,
求实数m的值。 解法一:已知圆的圆心为O( 0, 0), 半径r =1,
则O到已知直线的距离
由已知得 d=r , 即
解得 m=④试解本节引言中的问题. 解:以台风中心为原点,东西方向为x 轴,建立如图所示的直角坐标系,其中,取10km为单位长度,这样,受台风影响的圆形区域所对应的圆O方程为
轮船航线所在直线L的方程为4x+7y-28=0
?问题归结为圆O与直线L有无公共点。
点O到直线L的距离
圆O的半径长r=3
因为3.5>3,所以,这艘轮船不必改变航线,不会受到台风的影响.
xy0AB1、直线和圆相离2、直线和圆相切3、直线和圆相交直线与圆的位置关系图形圆心到直线距离 d 与圆半径r之间关系几何方法代数方法无交点时有一个交点时有两个交点时课堂总结 作业: 习题 4.2
第3题 第5题归纳小结1:过圆x2+y2=r2上一点(xo,yo)的切线方程为xox+yoy=r2
2:过圆(x-a)2+(y-b)2=r2上一点(xo,yo)的切线方程为(x-a)(x-x0)+(y-b)(y-y0)=r2
3:过圆x2+y2=r2外一点(xo,yo)的作圆的切线,两切点的连线的直线方程为xox+yoy=r2
4:过圆(x-a)2+(y-b)2=r2外一点(xo,yo)的作圆的切线,两切点的连线的直线方程为
(x-a)(x-x0)+(y-b)(y-y0)=r2
补充习题.己知圆C: x2+y2-2x-4y-20=0,
直线l: (2m+1)x+(m+1)y-7m-4=0(m∈R)
(1)证明: 无论m取何值 直线l与圆C恒相交.
(2)求直线l被圆C截得的最短弦长,及此时
直线l的方程.分析: 若直线经过圆内
的一定点,那么该直线
必与圆交于两点,因此
可以从直线过定点的角
度去考虑问题. 提高练习 解 (1)将直线l的方程变形,得
m(2x+y-7)+(x+y-4)=0.
∵对于任意的实数m, 方程都成立,此时l方程 y -1 = 2 (x - 3),即 2x-y-5=0
